保持架与外圈引导间隙的计算
2013-07-21李秋萍张伟梁培栋范雨晴
李秋萍,张伟,梁培栋,范雨晴
(1.中铝洛阳铜业有限公司,河南 洛阳 471039;2.洛阳轴研科技股份有限公司,河南 洛阳 471039;3.哈尔滨工业大学,哈尔滨 150001)
符号说明
Bc——保持架宽度
Dcp——保持架兜孔中心圆直径
Dpw——球组节圆直径
E——弹性模量
F——保持架的离心力
m——保持架质量
Rce——保持架外半径
Rci——保持架内半径
To——轴承工作温度
Ta——环境温度或标准温度
u——保持架半径增加量
v——保持架线速度
ρ——保持架材料密度
ω——保持架角速度
σr——径向应力
σt——切向应力
εr——径向应变
εt——切向应变
ν——泊松比
ΔDc——保持架的引导间隙
ΔDc1——离心力作用下保持架外径的增大量
ΔDc2——温升膨胀下保持架外径增大量
ΔD2——温升膨胀下外圈内径的增大量
Γc——保持架材料线膨胀系数
Γw——外圈材料线膨胀系数
对于外圈引导保持架的轴承,保持架的引导间隙极为重要,如果引导间隙太小,保持架外径与外圈内径会发生严重摩擦,影响两者间润滑油膜的形成,产生噪声和温升,严重影响轴承的使用寿命;如果该间隙太大,则保持架旋转轨迹不规则,会产生噪声和振动,影响保持架的使用寿命。下文将基于理论力学与材料力学,对保持架的受力进行分析,并结合轴承工作温度变化对保持架尺寸的影响以及轴承的应用经验,给出外圈引导保持架引导间隙的计算方法。
1 引导间隙的计算方法 [1]
在对保持架进行受力分析时,视其为圆环体,如图1所示。保持架高速旋转下的离心力为
(1)
离心力作用下的径向应力
(2)
如图1所示,平衡条件下作用在面积单元dRdφ上的径向合力为零,即
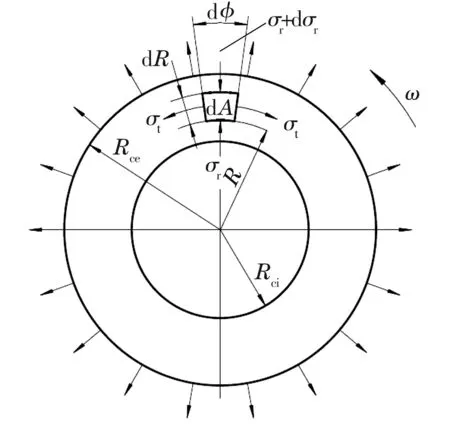
图1 离心力下保持架圆环体受力
(3)
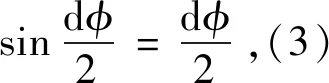
(4)
由于径向应力的作用,保持架半径增大量为u,则径向方向的单位应变为
(5)
圆周方向的单位应变为
(6)
根据平面应变理论
(7)
(8)
由(5)~(8)式得
(9)
(10)
将(9)~(10)式代入(4)式得
(11)
(11)式的通解为
u=aR+bR-1。
(12)
将(12)式代入(9)~(10)式得
(13)
(14)
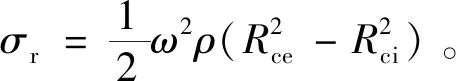
(15)
求解(15)式得
(16)
(17)
将(16)~(17)式代入(13)~(14)式,得
(18)
(19)
将(18)~(19)式代入(8)式可得

(20)
由(20)式和(6)式得保持架半径的增大量为
(21)

(22)
由(21)~(22)式得出离心力作用下保持架外径的增大量为
(23)
轴承在实际工作时,保持架温度高于外圈温度,保持架温升膨胀下外径的增大量为
ΔDc2=2ΓcRce(To-Ta),
(24)
轴承外圈温升膨胀下内径的增大量为
ΔD2=2ΓwR2(To-Ta),
(25)
由于保持架与外圈间的引导间隙很小,可以认为R2≈Rce,则(25)式变为
ΔD2=2ΓwRce(To-Ta)。
(26)
根据经验,对于保持架外径小于250 mm的轴承,在工作时保持架外径与外圈内径的间隙为0.1~0.2 mm时最佳, 所以引导间隙为
ΔDc=ΔDc1+ΔDc2-ΔD2+(0.1 ~0.2 )。
(27)
2 实例
利用上述公式分析计算H71916C/P4轴承保持架的引导间隙。根据设计要求Dpwn=2.5×106mm·r/min。保持架各参数值分别为Rce=50.1 mm,Rci=46.95 mm,Dcp=95.2 mm。保持架材料为PA66(尼龙),其弹性模量E=8.3 GPa,泊松比ν=0.28,密度ρ=1 145kg/m3,热膨胀系数Γc=6×10-5℃-1;轴承外圈材料的热膨胀系数Γw=1.2×10-5℃-1;Ta=20 ℃,To=65 ℃。
由(23)~(24)式和(26)式分别得ΔDc1=0.24 mm ,ΔDc2=0.11 mm ,ΔD2=0.05 mm。则,由(27)式得ΔDc=0.4~0.5 mm,取ΔDc=0.45 mm。
3 试验验证
由于兜孔的存在使得保持架为非均质实体,如果按均质实体对其进行分析,有可能在受力方面会存在较大误差,从而影响计算结果的正确性,所以需要加以验证。
H71916C/P4轴承为油气润滑,其保持架结构如图2所示。保持架与外圈不同引导间隙下的试验结果见表1。
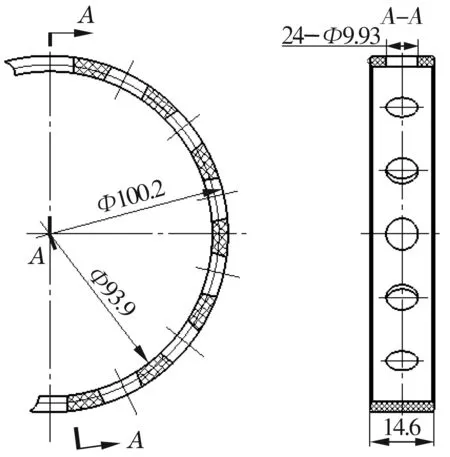
图2 H71916C/P4保持架外形尺寸
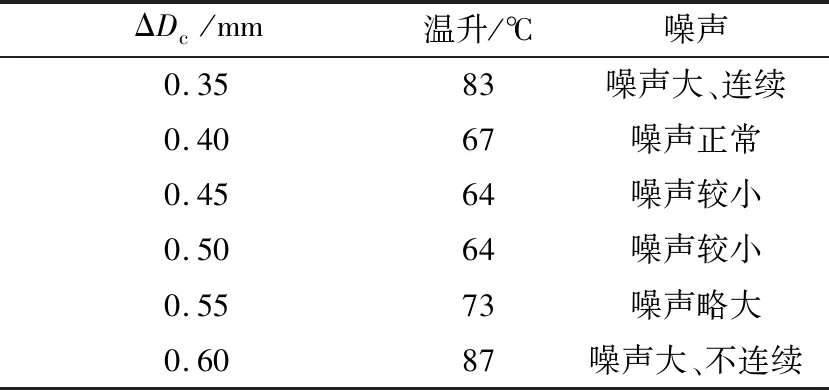
表1 不同引导间隙下的试验数据
由表1可知,轴承采用由文中计算方法得出的引导间隙(0.45 mm)时,噪声小、温升低,满足轴承的性能要求。
4 结束语
基于理论力学与材料力学,推导出了外圈引导保持架引导间隙的计算关系式。在轴承设计时,可根据保持架尺寸、轴承转速、工作温度和材料等因素计算出合理的引导间隙,以满足轴承振动、噪声、温升、极限转速和寿命等性能指标的要求。
