基于研究性学习的数学分析教学实践
2013-07-20葛仁福
葛仁福
(连云港师范高等专科学校 数学系,江苏 连云港 222006)
1 引 言
《国家中长期教育改革和发展规划纲要(2010—2020年)》中明确指出,高等教育要“着力培养信念执著、品德优良、知识丰富、本领过硬的高素质专门人才和拔尖创新人才”,研究性学习和研究式教学对于培养高素质研究型创新人才具有重要的意义.研究性学习是指学生在教师指导下,选择和确定研究专题,主动地获取知识、应用知识、解决问题的一种学习方式[1].研究性学习的核心在于“要让学生感受、理解知识的产生和发展过程”,培养学生收集处理信息的能力、获取新知识的能力,引导学生创造性地运用知识和能力,综合运用研究方法,以达到培养学生的科学精神和创新思维的目的.研究式教学是教师在组织教学活动的过程中,不断渗透科学研究的方法,以做研究的方式,引导学生学会用数学的思维发现问题并解决问题[2].“数学分析”是高等师范院校数学专业的核心基础课之一,它蕴含着深刻的数学思想方法,同时由于其概念性强、内容高度抽象以及逻辑推理严谨等特点,在培养学生的数学素养、抽象思维和逻辑推理方面起到重要作用,但同时也给学生的学习带来困难,传统的数学分析课程教学只管讲授“是什么”,而忽略了解决“为什么是什么”、“是什么会引起什么”以及“不是什么会是什么”等问题,同时也忽略了学生的创造性思维的发展,因此,在数学分析课程教学中要开展研究式教学,更有利于学生创新性思维的培养.
2 数学分析中概念的研究式教学
数学分析中的概念具有很强的“实践性”特征,因为许多概念来源于生活实践,从生活实践中抽象出来而形成数学结构,这种数学结构是抽象的,是以“模式”的形式而存在的,并且以符号语言形式来表达的,因此学生不易理解和掌握.数学模式观认为,数学是关于模式的建构与研究,数学的学习就是构建模式,研究和应用模式,研究式教学的核心在于“研究”模式,教师要以模式的观点来指导和组织教学,通过自己对教学的组织为学生展现出生动的数学思维活动过程,从而帮助学生逐步培养识别模式、建构模式、发展模式的能力.
数列极限概念是数学分析中最基础也是最重要的基本概念,其定量化定义就是模式的体现,即

传统的教学设计是以“通过对ε的具体取值找出N”,即归纳法来抽象出数列极限的定量化定义,基于研究性学习和教学的视角,该如何教会学生理解、掌握并运用极限概念呢?
(1)识别模式阶段.识别模式就是让学生掌握数学极限定量化表述的方法.
思考2:ε、N和n都代表什么?含义是什么?起什么作用?
通过上述两道思考题,学生会识别出数列极限概念定量化模式的含义,逻辑上更清晰,更明确每一句话蕴含的意义.
(2)建构模式阶段.建构模式是让学生对数列极限定量化表述的结构认识更加清晰,从而在头脑里形成牢固认知,并达到掌握.
思考3:四段话中的各句位置是否可以调换?
思考4:四段话中的“>”和“<”是否可以换成“≥”和“≤”?
思考5:数学极限概念如何用几何语言来表述?即“对∀ε>0,邻域U(a,ε)内(外)含有数列{an}的无限(有限)多项”是否正确?
(3)发展模式阶段.发展模式就是在学生已经理解掌握概念结构的基础上,对一些相关问题进行辨别,达到运用的目的.
思考7:若对ε=1,则 ∃N∈N,对 ∀n>N,有an∈(a- 1 ,a+1)或 |an|<|a|+1,说明什么?由此能得到什么结论?

思考10:若子数列{a3k+1},{a3k+2},{a3k}都收敛,则数列{an}是否收敛?
思考6–10的设计是让学生在掌握数列极限概念模式的基础上进一步发展模式,带领学生进入深层次思考,达到灵活运用极限概念模式的目的.
3 数学分析中定理的研究式教学
数学分析中的定理在数学分析学习中占有重要地位,理解、掌握定理内容不仅是学生学习数学分析课程的基本要求,而且是学生加深掌握知识体系、培养推理能力,提高数学素养的重要手段,但由于数学定理本身的抽象性、独特性和证明方法(如构造性、模式化等)表现出来的复杂性,也要求学生在学习和教师的传授中开展研究性学习和研究式教学.定理的研究式教学核心在于指导学生掌握定理的证明方法的选择和运用以及定理内容的扩展上,通过掌握证明方法达到举一反三的目的,通过研究定理内容的扩展培养学生的创造性思维,这两个环节的实现一般通过两步走.在第一环节证明方法的运用部分宜采用波利亚的“怎样解题”给出的“四个阶段”进行[3];第二环节需要变换命题的必要条件、充要条件以及更改条件等方式来探讨定理内容的扩展.
3.1 证明方法的选择和运用
理解题目:明确定理所给出的已知条件和要证明的目标;
拟定方案:找到定理条件所能提供的信息或推断或数据,寻找证题思路和路径,建构已知信息与求证目标之间的联系;
执行方案:按照证题思路,把推理落实到每一步骤,看每一步骤是否正确,并向目标前进;
回顾反思:回头考察总结论证所使用的方法是否准确?是否具有推广性?
拟定方案是完成定理证明的关键部分,“思路决定出路”,思路正确、路径正确,便容易证出结论,教师要教给学生的真正的“渔”就在这里,“暴露思维过程”也就在这一阶段,教师要用合理的分析在学生头脑中搭建起由已知通向目标的桥梁.
以数学分析中定理“闭区间上的函数连续必有界”的教学设计为例.第一阶段和第二阶段思维过程简略为如图 1(采用直接证法).
拟定出的方案是否准确可行还需要在执行方案的过程中加以验证,执行方案是完成定理证明的核心部分,即要把拟定的方案转化为符合逻辑推理的文字表述,写出具体的证明过程.在此过程中有很多细节问题需要处理,也需要教师在教学中加以阐明.鉴于教科书上有具体证明过程,此处略.
此定理的证明中运用了有限覆盖定理,在回顾反思阶段需要思考的是:(1)有限覆盖定理在本证明中起到了什么作用,如果不使用有限覆盖定理还可以运用什么定理,运用其它定理是否可以证明;(2)在执行方案中每一步推断是否为真,是否达到了要证明的结论,中间有没有漏洞;(3)此定理是否可以采用间接证法,若采用间接证法其方案该如何拟定等(用反证法和区间套定理可证,此处略).
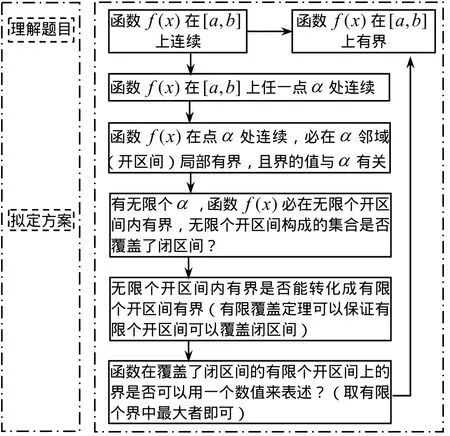
图1 “闭区间上的函数连续必有界”的第一阶段和第二阶段思维过程
3.2 定理内容的扩展训练
学习定理既要兼顾学习定理本身的意义,更要重视学习定理所引申出的一些让人会更深入思考的数学事实.此定理在研究式教学中还应挖掘其拓展意义,基于“不满足定理条件会有什么结论”和“满足定理条件还会有什么结论”给出如下思考:
思考1:若函数f(x)在(a,b)上连续,则函数f(x)在(a,b)上是否有界?
思考2:若函数f(x)在闭区间[a,b]上有定义,则函数f(x)在(a,b)上是否有界?
思考3:若函数f(x)在(a,b)上连续,则增加什么条件可使得函数f(x)在(a,b)上有界?
思考4:若函数f(x)在(a,+∞)上连续,则函数f(x)在(a,+∞ )上是否有界?
思考5:若函数f(x)在[a,b]上连续,则函数f(x)在[a,b]上能否取到最大最小值?
只有通过这种拓展训练才能培养学生的创造性思维、增强学生推理能力和严谨的科学态度.
4 数学分析中习题的研究式教学
习题教学是数学分析教学的重要组成部分,在数学分析课程中常设置专门的课时来处理习题,有的习题对于学生来说是新知识或是有难度的,需要教师在习题课上开展研究式教学,组织学生开展研究式学习.研究式教学的宗旨就是让学生参与,学生亲自实践,亲自参与研究,教师帮助学生解决疑难,掌握知识.
案例1:在学生学习了“函数列一致收敛[4]”一节后,学生在头脑里形成了关于函数列一致收敛的概念,及如何判别函数列一致收敛的充要条件,教师需要进一步指导学生思考[5]:
若函数列在区间I上一致收敛(不一致收敛),那么在子区间I1⊂I或I2⊃I上函数列的一致收敛性如何?
若函数列在区间I上一致收敛(不一致收敛),那么在相邻区间I1上上函数列的一致收敛性如何?
下列命题是否正确:
命题2:若函数列在区间I上一致收敛,则在其内部任意子区间上也一致收敛.
案例2:判别下列函数列的一致收敛性[6]:(1),x∈[0,1];(2),x∈ [-l,l];;(4)x∈ [0,+∞)(解答略).可以看出,这几个例子表达形式似乎相同,但实质不同,其一致收敛性也不尽相同(如图2~图5).
通过研究函数列的图象特征,以及通过函数列一致收敛的充要条件的判别,学生进一步加强了对函数列一致收敛性的认识,同时既加强了对判别方法的熟练掌握,也培养了细致耐心的治学态度.
提出一个问题往往比解决一个问题更重要,研究性学习就是要求学生积极思考问题,研究式教学就是要求教师积极提出问题,指导学生思考[7].善于发现问题,提出问题,是一切创新过程的基础,也是富有创新精神的人所必须具备的一种能力.从以上讨论可以看出,在数学分析课程教学中开展研究性学习和研究式教学都是非常必要和重要的.

图2 f(x ) = 图象n
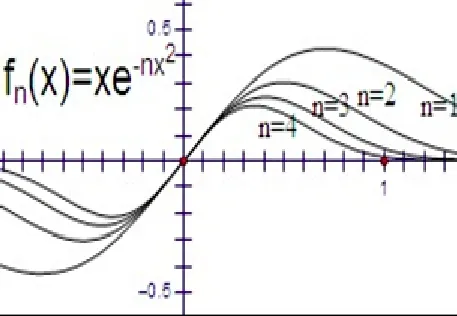
图3 f(x ) = 图象n
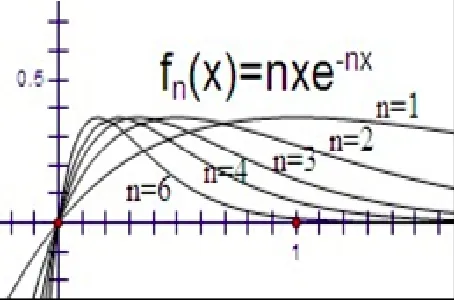
图4 f n (x ) =nxe-nx图象
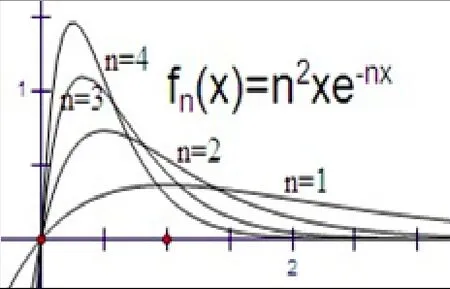
图5 fn (x)= n 2xe-nx图象
[1]李星云.小学数学专题研究[M].苏州:苏州大学出版社,2001.
[2]王显金.高效教学策略:我对数学研究式教学的一点理解[J].宁波大红鹰学院学报,2010,(4):98–101.
[3]G·波利亚.怎样解题[M].上海:上海科技教育出版社,2002.
[4]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.
[5]刘秀梅.函数列在不同区间上一致收敛性的研究[J].大学数学,2008,28(6):160–164.
[6]刘秀梅.一类函数列一致收敛性的研究[J].赤峰学院学报(自然科学版),2007,23(1):7–9.
[7]王雪琴.发散思维是培养学生数学创新精神的突破口——数学分析习题课教学感悟[J].数学教育学报,2012,21(4):83-86.
