初中生数学自我概念对数学成就影响机制的研究

2013-07-20梁好翠

数学教育学报 2013年1期

梁好翠

（钦州学院数学与计算机科学学院，广西钦州 535000）

1 问题的提出

自我概念是指由个体对自身的观念、情感和态度组成的混合物，是个体对自己的综合看法．学生的自我概念由学业自我概念和非学业自我概念组成，学业自我概念可分语文自我概念、数学自我概念等具体学科自我概念．学业自我概念是指个体在学业情境中形成的对自己在学业发展方面的比较稳定的认知、体验和评价[1]．数学自我概念是指学生在学校情境中形成的对自己在数学学业方面的特长、能力和知识形成的比较稳定的认知、体验和评价，它是学生自我意识中的数学自我的知觉和评价，是学生通过对数学活动、自我属性和社会环境的经验体验及对经验理解而形成的[2]．

有关研究表明，学业自我概念与学业成绩之间存在密切的关系[3～6]．不同数学学习水平的初中生的数学自我概念存在非常显著的差异，优生明显高于差生[2]．数学自我效能和数学自我概念对数学学业成绩具有较强的预测作用[7～8]．在国外，探讨得最多也是最关键的问题之一就是确立学业自我概念与学业成绩之间因果关系的顺序，到目前为止，已形成了解释其因果关系的几种理论模型[1]，即自我增强模型（self-enhancement model）、技能发展模型（skilldevelopment model）、交互影响模型（reciprocal-effect model）、发展观（development perspective）等．自我增强模型认为，学业自我概念是学业成绩的决定因素，即先前的学业自我概念影响随后的学业成绩．因为学业自我概念具有动机性质，所以学业自我概念的改变将引起学业成绩的改变．技能发展模型认为，学业自我概念是学业成绩的结果，即先前的学业成绩影响随后的学业自我概念．交互影响模型是技能发展模型与自我增强模型之间的一种折衷模型，认为学业自我概念既影响学业成绩，同时又受学业成绩的影响．这种模型有一个重要的推论就是把学业自我概念作为一种有助于其它预想结果的手段，同时也作为一种重要的结果变量．发展观认为，随着学生年龄的增长，其因果关系顺序也发生着变化，对于年幼儿童来讲，二者关系主要表现为技能发展模型，而对于年长儿童和青少年来讲，二者关系主要表现为自我增强模型和交互影响模型．上述这些关系模型都是国外学者提出的关系理论模型，由于中外的文化、思维等差异，这些关系模型是否符合我国中小学学生的情况？具体到数学学科方面，这些关系模型是否也适用？数学自我概念是否对数学成绩产生影响？数学自我概念对数学成绩的影响是否通过数学学习动机起作用？这些都有待进一步研究，特别是实证研究．

在强调教会学生如何学习的今天，学习动机及其培养在教育界中倍增关注．在非认知因素中，学习机动对数学学习影响较大[9]，而且学习动机与数学自我概念存在显著的正相关[2]．因此，研究者引入数学学习动机作为中间变量，以初中生为研究对象，采用测量问卷调查、访谈等方法对初中生数学自我概念如何影响数学学习成绩进行研究，探讨初中生数学自我概念、数学学习动机与数学学习成绩之间的关系，分析数学自我概念、数学学习动机对数学学习成绩的影响程度，以及数学自我概念对数学学习成绩的影响是否通过数学学习动机起作用，进一步分析数学自我概念与数学学习成绩的关系模型，为提高初中生数学自我概念，以及帮助学生认识自我和建立数学自信心提供一些理论的参考．

2 研究方法

2.1 被试

选取某省市两所普通中学共810名初中生作为被试，有效被试共801人．

2.2 研究工具

（1）数学自我概念量表．采用Marsh（1992）的自我描述问卷Ⅱ．自我描述问卷Ⅱ的适用范围是7～10年级的中学生．该量表共有11个分量表，102道测试题组成．其中包括 3个学业自我概念（言语、数学和一般学校情况）和 7个非学业自我概念及1个一般自我概念．陈国鹏对此量表进行了修订，各分量表的内在稳定性系数在0.83～0.91之间．各分量表的重测信度在0.72～0.88之间．11个分量表的相关系数大多在 0.40以下，彼此之间相关不高，说明各分量表可以独立使用．从中抽取出与数学有关的10个题目构成《数学自我概念量表》．如“我的数学总是很好”、“我很想上数学课”等．这10个题目将数学自我概念划分为两个维度：能力维度和情感维度．供选支从“完全不符合”到“完全符合”共5项，采用5点计分法．经研究，本量表的克伦巴赫系数为0.876，具有较高的信度．

（2）数学学习动机量表．根据数学学科特点和初中生的情况，我们依据成就动机理论，主要考虑成绩目标取向和学习目标取向设计量表．量表由8道选择题组成，采用5点计分法，克龙巴赫系数为0.824．

2.3 研究程序和数据处理

（1）问卷调查在统一的指导语下进行，时间为 20分钟．采用随机整群抽样的方法，发放810份问卷，最后收回有效问卷801份．其中初一、初二、初三分别为268、268、265份；男女分别为399、402份．

（2）数学成绩是以数学期终考试成绩作为学生数学学习成绩．将被试的数学学习成绩由高到低排序，按总人数的25%、50%、25%分为优生组（200人）、中等组（401人）和差生组（200人）．

（3）所有的数据采用SPSS17.0 for Windows进行数据处理和统计分析．

3 结果与分析

3.1 数学自我概念和数学学习动机与数学成绩相关性分析

对数学自我概念、数学学习动机、数学学习成绩之间进行相关性分析，结果如表1所示．由表1可知，数学自我概念、数学学习动机、数学学习成绩之间都存在非常显著的正相关（P<0.01），这说明，数学自我概念、数学学习动机、数学学习成绩之间存在密切的关系．

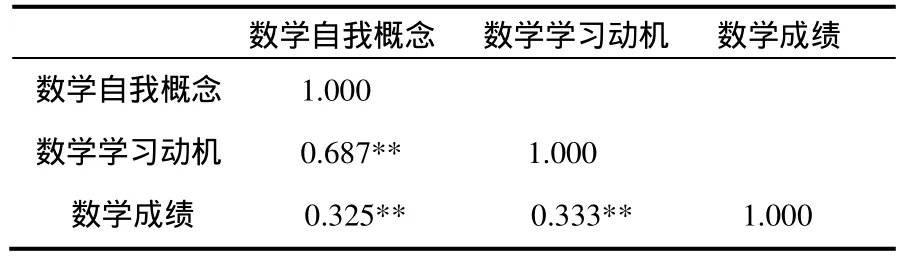
表1 数学自我概念和数学学习动机与数学成绩相关分析

3.2 优差生组在数学自我概念和数学学习动机水平上的比较

为考察优生组和差生组在数学自我概念和数学学习动机水平上的差异情况，对其进行t检验，结果如表2．由表2可知，优生与差生在数学学习动机、数学自我概念两个维度及总体水平上都存在非常显著的差异（P<0.01）．优生的数学自我概念和数学学习动机明显高于差生．

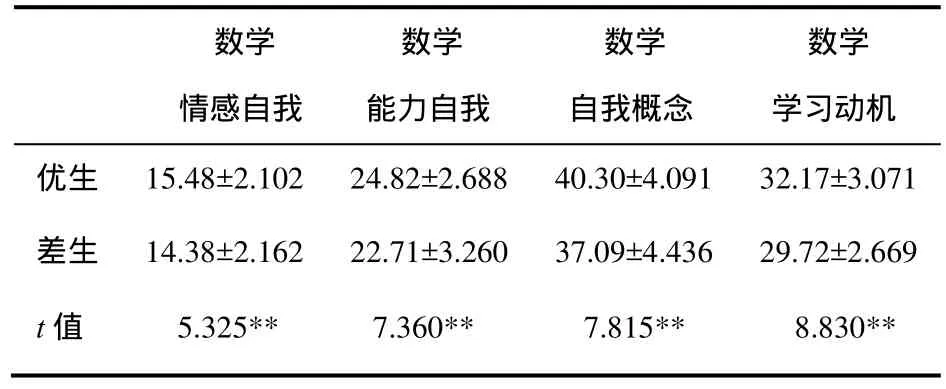
表2 优差生组数学自我概念和学习动机水平比较表（M±SD）

3.3 数学自我概念与数学学习动机对数学成绩的回归分析

为了进一步探讨这两类因素对数学学习成绩的影响程度，我们将数学自我概念、数学学习动机对数学学习成绩进行二元回归分析．结果如表3．

由表3可知，两个变量的标准偏回归系数分别是0.183和 0.208，且两者的β值均具有非常显著的统计学意义（P<0.01）．这一结果说明，两者对数学学习成绩都具有预测作用，数学学习动机比数学自我概念对数学学习成绩的影响程度要大．

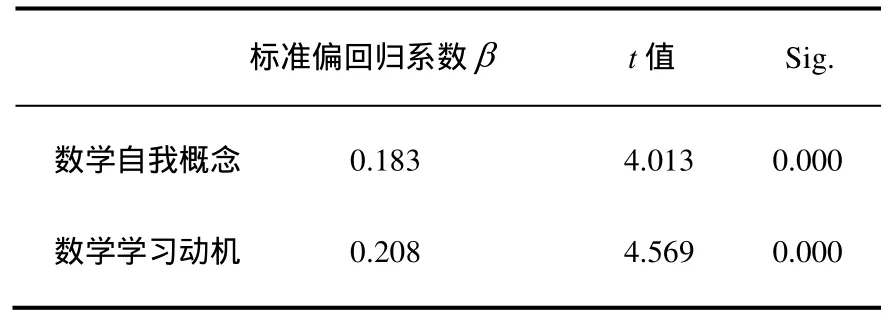
表3 数学自我概念与数学学习动机对数学成绩的二元回归分析

3.4 数学自我概念和数学学习动机对数学成绩影响的路径分析

以数学自我概念为预测变量，以数学学习动机为因变量进行一元回归分析，主要结果是：标准回归系数β为0.687（t=27.732**），决定系数R2为 0.472，这说明数学自我概念可以解释数学学习动机47.2%的变异．再根据上述的二元回归分析的结果所得到的标准回归系数即路径系数β和决定系数R2=β×r，其中r为相关系数，建立影响路径模型，结果如图1（括号内为决定系数）．由图1可知，数学自我概念和数学学习动机可以解释数学成绩12.8%的变异，数学自我概念和数学学习动机对数学成绩有显著的回归效应．

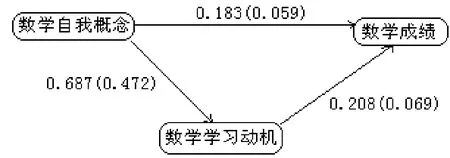
图1 数学自我概念和学习动机对数学成绩影响路径模型

3.5 数学学习动机在数学自我概念对数学成绩影响中的中介效应分析

中介效应的定义是，自变量X对因变量Y的影响，如果X通过影响变量M来影响Y，则称M为中介变量．假设所有变量都已经中心化，可用下列方程来描述变量之间的关系：Y=c1X+e1、M=aX+e2、Y=c2X+bM+e3．中介作用的前提条件是自变量X、因变量Y和中介变量M两两之间有显著的相关．

在上面的相关分析中，数学自我概念、数学学习动机和数学成绩两两之间存在显著的正相关，因此满足中介作用的前提条件．下面，根据文[10]提出的中介效应的检验程序进行检验，检验数学学习动机M在数学自我概念X和数学成绩Y之间是否起着中介效应．结果如表4．

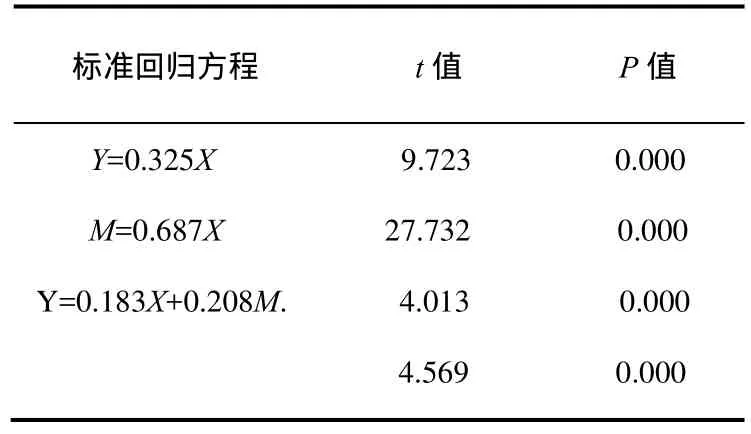
表4 数学学习动机的中介效应检验

由表4可知，由于依次的t检验的结果显著，因此数学学习动机的中介作用显著．同时，由于c2=0.183这一标准回归系数显著，所以只是部分中介效应，并且中介效应占总效应的比例为因此，数学自我概念对数学成绩的影响并不是全部以数学学习动机为中介作用，只是有部分的中介效应．即数学自我概念对数学成绩的影响，一方面是直接的，另一方面是部分通过数学学习动机起作用．

4 讨论

4.1 数学自我概念与数学学习动机的关系

研究结果表明，学生的数学自我概念与数学学习动机存在显著的正相关．在访谈时也发现，对自己的数学学习能力有自信，并且有较好的自我价值感的学生，也具有较高的数学学习兴趣和积极的学习动机；对自己的数学学习能力的自信心不足或较弱的数学情感的学生，他的数学学习兴趣和学习动机也就较低．当个体形成一定的数学自我概念后，他就倾向于产生与这一概念相一致的行为方式，数学自我概念实际上起着学生数学学习行为自我调节与定向的作用，影响着学生数学学习的积极性[2]．因此，学生的数学自我概念对数学学习动机产生重要的影响．一般地，即具有较高的数学自我概念的学生倾向于具有积极的数学学习动机，具有较弱的数学自我概念的学生倾向于具有消极的数学学习动机．

4.2 初中生数学自我概念与数学成绩的关系

研究发现，初中生数学自我概念与数学学习成绩之间的影响具有双向性和动态性，初中生数学自我概念与数学成绩的因果关系主要表现自我增强模型、交互影响模型及发展观等．

一方面，初中生的数学自我概念对数学学习成绩产生重要的影响，即具有较高的数学自我概念的学生倾向于具有优秀的数学学习成绩，具有中等水平的数学自我概念的学生倾向于具有中等的数学学习成绩，具有较弱的数学自我概念的学生倾向于具有较差的数学学习成绩．另一方面，初中生的数学学习成绩对数学自我概念也产生重要的影响，即不同数学学习成绩水平的初中生数学自我概念存在非常显著的差异，优生、中等生、差生两两之间的差异达非常显著的水平．数学学习成绩优异的学生大多有较高的数学自信，维持着较高数学自尊；数学学习成绩较差的学生大多有较低的数学自信，表现出数学自信心不足[11～21]．通过访谈了解到，对于初一学生，大部分学生先前的数学自我概念影响随后的数学学习成绩，具有自我增强模型的特点；初二学生的情况比较复杂，部分学生具有自我增强模型，也有部分学生具有交互影响模型的特点；初三大部分学生的数学自我概念既影响数学学习成绩，同时又受数学学习成绩的影响，具有交互影响模型的特点．整个初中阶段表现出发展观的特点．这可能与初中阶段学生的心理成熟度有关，也与数学的严谨性、抽象性和符号化等特征有关．

5 结论

（1）初中生数学自我概念、数学学习动机和数学学习成绩之间都存在非常显著的正相关，它们之间存在非常密切的关系．

（2）初中生数学自我概念与数学学习成绩之间的影响具有双向性和动态性，初中生数学自我概念与数学学习成绩的因果关系主要表现为自我增强模型、交互影响模型及发展观等．大部分初一学生先前的数学自我概念影响随后的数学学习成绩，具有自我增强模型的特点；初二的部分学生具有自我增强模型，部分学生具有交互影响模型的特点；大部分初三学生的数学自我概念既影响数学学习成绩，同时又受数学学习成绩的影响，具有交互影响模型的特点．整个初中阶段表现出发展观的特点．

（3）数学自我概念和数学学习动机对数学学习成绩都产生重要的影响，两者对数学学习成绩都具有预测作用，数学学习动机比数学自我概念对数学学习成绩的影响程度大．数学自我概念对数学成绩的影响并不是全部以数学学习动机为中介作用，只是有部分的中介效应，中介效应占总效应的比例为43.97%．因此，数学自我概念对数学成绩的影响，一方面是直接的，另一方面是部分通过数学学习动机起作用．

（4）优生与差生在数学自我概念和数学学习动机上存在显著的差异．优生的数学自我概念和数学学习动机明显高于差生．

[1]郭成，何晓燕，张大均．学业自我概念及其与学业成绩关系的研究述评[J]．心理科学，2006，29（1）：133-136．

[2]梁好翠．初中生数学自我概念的调查与分析[J]．数学教育学报，2010，19（2）：42-45．

[3]李叶，田学红．初中生学业自我概念与学业成就的相关研究[J]．湖北民族学院学报（哲学社会科学版），2002，20（3）：76-79．

[4]徐富明，施建农，刘化明．中学生的学业自我概念及其与学业成绩的关系[J]．中国临床心理学杂志，2008，16（1）：59-62．

[5]姚计海，屈智勇，井卫英．中学生自我概念的特点及其与学业成绩的关系[J]．心理发展与教育，2001，17（4）：57-64．

[6]周琳．初中生数学焦虑、数学学业自我概念及其对数学成绩的影响[D]．河南大学，2008．

[7]刘喆．大学生数学自我效能、自我概念与数学学业成绩关系的研究[J]．数学教育学报，2009，18（6）：37-41．

[8]田仕芹．高等数学学习自我效能感的调查分析[J]．数学教育学报，2011，20（5）：66-69．

[9]喻平．数学教育心理学[M]．南宁：广西教育出版社，2004．

[10]温忠麟，张雷，侯杰泰，等．中介效应检验程序及其应用[J]．心理学报，2004，49（4）：614-620．

[11]纪红军，李颖慧，司继伟．结合“元认知训练”和“学习动机”激发促进初中生的数学学习[J]．数学教育学报，2009，18（4）：93-98．