HPM与初中数学教师的专业发展:一个上海的案例
2013-07-20汪晓勤
汪晓勤
(华东师范大学 数学系,上海 200241)
HPM是数学教育的一个研究领域,2005年至今连续4届全国数学史与数学教育会议使得HPM逐渐为国内学术界所熟悉,但学术研究与课堂实践之间的鸿沟使得数学史在中学“高评价、低应用”的境遇迄今并未得到实质性的改善.要让HPM真正走进课堂,就必须有中学教师通过专业发展进入HPM学术共同体.那么,HPM介入数学教学,能带给教师什么样的变化?HPM 究竟能否促进教师的专业发展?研究试图对上述问题作出回答.
1 研究方法
1.1 研究的参与者
研究的参与者 J是上海某初级中学的一名数学教师,2001年毕业于一所师范学院,大学期间并未修读过数学史课.在 7年的教学生涯中,J教师积累了丰富的教学经验,“对初中数学的教材、教法、考试都非常熟悉”,但从未在课堂上用过数学史.J教师于 2009年开始在某师范大学攻读教育硕士学位,有机会在暑期里修读“数学史与数学教育”课程(框架如图1所示).首次接触数学史及其与数学教学的关系,对其产生了浓厚的兴趣,用她自己的话说:“学了20几年的数学,教了7年的数学,原来对数学中那么宝贵的一角竟是如此陌生,当时既惭愧又兴奋.暑假结束后回到三尺讲台,再也不忍心将这么宝贵的教学资源置之不理.”新学期伊始,J教师开始实施数学史融入数学教学的行动研究计划,由此成为研究的参与者.

图1 “数学史与数学教育”课程框架
1.2 资料的收集
研究的资料通过以下途径收集.
(1)HPM教学设计与教学反思的收集.J教师在以“计划—行动—观察—反思”为基本流程的行动研究过程中,对融入数学史的每一节课都有基于学生反馈(通过问卷调查和访谈获得)的教学反思,从这些反思中可以看到她在 HPM介入教学之后的心路历程.
(2)课堂观察与录像研究.J教师开设的部分公开课的课堂观察和录像文字整理由研究生完成.
(3)J教师在区教研活动中的演讲.J教师所在区的教育局承担了全国教育科学“十一五”规划教育部重点课题“提升中小学生学业效能:‘轻负担、高质量’的实证研究”,在该课题的研究过程中,教育局实施了一项在全区范围内征集“课堂增值”案例的活动.J教师撰写的案例“利用数学史,激发火热思考”在总共2 072篇案例中脱颖而出,被评为优秀案例;最终她作为唯一一位数学教师参加“中学课堂增值行动专题论坛”演讲赛.她的演讲成了研究的资料.
(4)对J教师与她所在学校的教研组长、所在区的教研员的非结构式访谈.参加上面提到的论坛时,研究者针对J教师的专业成长,对教研员、教研组长进行了访谈,了解她的教学风格、学生与同事对她的评价、她所任教班级的学习状态等.
2 数学史融入初中数学教学的实践
如何将数学史融入数学教学?Fauvel总结出10种具体方式[1];Tzanakis和Arcavi归纳出3种方式[2]:一是提供直接的历史信息;二是借鉴历史进行教学,即发生教学法;三是开发对数学及其社会文化背景的深刻意识;而Jankvist则提出另外3种方式[3]:启发法、模块法和基于历史法.研究者将上述两种分类方法进行整合与改进,得到附加式、复制式、顺应式和重构式4类,见表1.

表1 数学教学中运用数学史的方式
根据表1的分类法,2009—2011年间J教师的HPM教学可以分为两个阶段.
2.1 第一阶段
在该阶段,J教师主要采用复制式,代表性案例为“相似三角形的应用”(共3节课).在第一节课,直接采用《九章算术》勾股章中的问题来讲授相似三角形的性质.
例1.今有邑方二百步,各开中门.出东门一十五步有木.问:出南门几何步而见木?
例2.今有山居木西,不知其高.山去木五十三里,木高九十五尺.人立木东三里,望木末适与山峰斜平.人目高七尺,问:山高几何?
例3.今有井径五尺,不知其深.立五尺木于井上,从木末望水岸,入径四寸.问:井深几何?
课堂练习题也直接取自《九章算术》勾股章,思考题则要求学生复原泰勒斯测量金字塔高度的方法.
第二节课先利用相似三角形性质解决《九章算术》的“勾股容方”问题(已知直角三角形的勾和股,求其内接正方形的边长),然后将问题拓广到一般三角形容方问题.
第三节课为拓展课,J教师先介绍公元前6世纪古希腊萨默斯岛上的引水隧道,引导学生展开讨论:设计者欧帕里诺斯(Eupalinos)究竟采用什么方法,确保南北两侧工程队沿同一直线向山体内部开凿,最后完美会合?学生讨论未果,J教师向学生讲解公元1世纪海伦(Heron)测量著作中的隧道设计方法,该方法正巧妙地利用了相似三角形的性质.
课后的问卷调查表明,84.4%的学生对数学史知识感兴趣;86.7%的学生认同数学史融入数学教学;93.3%的学生愿意了解数学史知识,并对数学史的作用给予积极的评价.受学生反馈的鼓舞,J教师决定继续她的HPM教学.
2.2 第二阶段
在与研究者、教研员交流讨论之后,她感觉到,尽管学生反响很好,但第一阶段的教学偏于“为历史而历史”,有很大的改进空间.在调往另一所初中之后,J教师开始了第二阶段的HPM教学,课型更丰富,方式更灵活多样,包括附加式、复制式、顺应式和重构式,代表性案例为“用字母表示数”、“同底数幂的乘法”、“平方差公式”等.
在“用字母表示数”一节,J教师利用英国幽默作家杰罗姆(J. K. Jerome)《懒人懒办法》中的片段引入课题,然后,再采用顺应式,将古希腊毕达哥拉斯学派的三角形数和正方形数改编成探究问题,通过让学生探究第n个点阵的点数,使学生理解“字母表示数”的意义,体会用字母表示数的重要思想.
在“同底数幂的乘法”一节,J教师采用重构式,通过古希腊数学家阿基米德(Archimedes)数沙问题(填满宇宙的沙粒数)来再现“幂”这个概念的发生过程,创造学生的学习动机,并从阿基米德在《数沙者》中所提出的以10为底的幂的乘法公式出发,导出以a为底的幂的乘法运算公式.
在“平方差公式”一节,J教师从三国时代数学家赵爽的故事引入,并采用复制式,用赵爽在“勾股圆方图注”中所用的图形导出平方差公式;再利用古巴比伦时期的数学问题(已知两个数的和与积,求这两个数)来说明平方差公式的应用.
这一阶段教学后的问卷调查表明,86.3% 的学生对数学史知识感兴趣;90.2%的学生认同数学史融入数学教学;96.1%的学生愿意了解数学史知识,并对数学史的教育价值给予积极的评价.
3 从诠释学循环看J教师的变化
科学史的诠释学循环最初由德国学者 Jahnke提出.Jahnke认为,从方法上看,科学史研究与其他历史研究一样,实质上是一种诠释工作,这种诠释工作具有假设甚至直觉的特征.科学史家对科学理论及其创建者做出诠释,而理论创建者本身又是所在领域的诠释者,无论是科学史家还是科学家,他们的诠释都经历“形成假设、检验假设和修正假设”的循环过程.如图2所示,科学家(S)对所在领域(O)进行诠释,建立科学理论(T);由S、T和O所构成的循环称为初圈.而科学史家(S1)对初圈进行诠释,构建科学史(T1);S1、T1和初圈构成的循环称为次圈.相应的数学史诠释学循环如图3所示,其中H为数学史家,M为古代数学家、O为数学对象,T为数学理论,I为诠释的结果——数学史.
Jahnke认为,如果数学教师要在课堂上运用数学史,他就必须进入数学史的诠释学循环之中[4]:在数学史家诠释结果(次圈)的指导下,设想自己进入生活在另一个时代、另一种文化的数学家的心灵之中,从而对有关领域作出自己的诠释(初圈),而这种诠释反过来又促进了对数学史家诠释结果的理解.
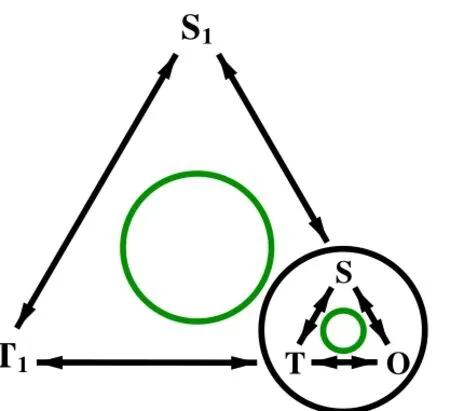
图2 科学史的诠释学循环图

图3 数学史的诠释学循环图
仿此,洪万生提出数学教学的诠释学循环[5],如图4所示.教材编写者(E)通过对课程标准与数学学科知识(S)的诠释,编成教材(C),E、C和 S构成初圈(C1);数学教师(T)设想自己进入教材编写者的心灵之中,对初圈进行诠释,确定教学内容知识(I),T、I和C1构成次圈.洪万生和苏意雯借助两种诠释学循环图,建立数学教师基于HPM 的专业发展模型[5~7].借鉴他们的方法,对 J教师的HPM教学的历程作一简略分析.
J教师走上教学岗位之后,有幸得到名师引领,钻研教材和教法,逐渐进入图4所示的T-C1-I循环之中.7年的教学实践让她积累了较为丰富的教学内容知识(PCK),用她自己的话说:“几个教学轮回下来,已经太熟悉哪一个知识点上该注意些什么.”但其中并不含有任何数学史知识.
在HPM介入教学的第一阶段,对数学史的浓厚兴趣以及与学生分享这种兴趣的强烈愿望使J教师很快进入图3所示的T-C2-I循环(其中C2为M、T和O构成的初圈).在“相似三角形的应用”的教学设计中,她确定了如下教学目标:
·了解《九章算术》和刘徽的相关知识与贡献,了解古希腊数学家几何学的鼻祖泰勒斯测量金字塔的故事,体会数学源于生活并服务于生活的道理.
·通过例题体会古人如何将实际问题转化为数学问题,并运用相似三角形的性质解决相关问题.
·通过数学史的引领与融入,提高他们的学习兴趣,增加他们的学习动机,改变学生的数学观.
可见,在这个阶段,J教师过于偏重数学史的教学,而忽略了原来的T-C1-I循环,换言之,她并未在C1和C2之间建立联系.
在HPM介入教学的第二阶段,基于学生与教师的反馈,以及与HPM研究者的深入交流讨论,J教师反思第一阶段的得失,对教学进行了较大的改进.如,在“同底数幂的乘法”的教学设计中,她确定了如下教学目标:
·知道幂的历史及幂出现的必要性,体会“同底数幂规律”的形成是源于实际问题的解决.
·通过推导同底数幂运算的性质形成抽象思维的能力.
·理解并掌握同底数幂运算的性质,并会文字语言与符号语言之间的转化.
·会运用同底数幂运算的性质进行相关计算.
同样是运用数学史,但 J教师不再在 T-C1-I和 T-C2-I两个循环之间顾此失彼,而是将两者融合在一起,换言之,在C1和C2之间建立起密切的联系,如图5所示.在这个阶段,教学不再为历史而历史,而是将历史和教材、课程标准有机地融合在了一起.
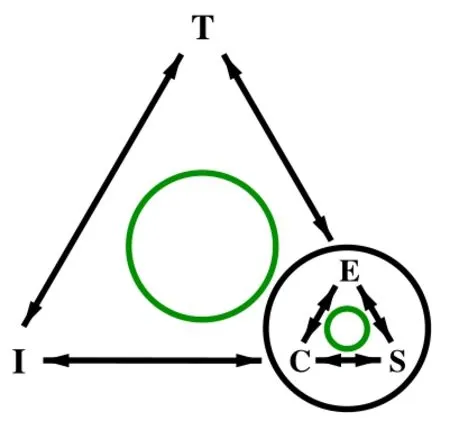
图4 数学教学的诠释学循环
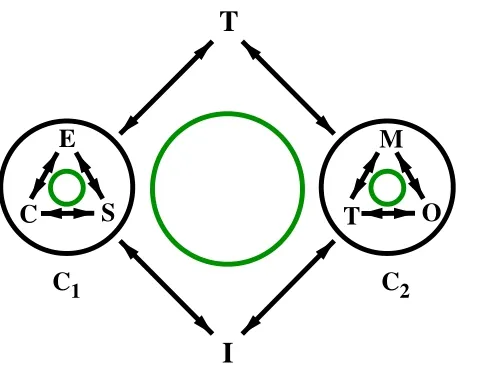
图5 基于HPM的新诠释学循环
4 初步的发现
通过课堂观察以及对于她本人、她的同事和区教研员的访谈,发现,经过两年的数学史融入数学教学的行动研究,J教师发生了很大的变化,主要体现在以下方面.
4.1 初步形成了自己的教学风格
对于一名教师来说,要形成自己的教学风格是十分不易的.J教师自己说:“在拥有 7年教龄之后,如果没有新的力量来推动,那么教师的教学瓶颈是很难突破的.”HPM引领她走进一片广阔的新天地,两种诠释学循环的融合导致了教学风格的逐渐形成.她的教学风格可用3个“一”来概括.
·一种超越.“无时间”、“无资料”、“无知识”、“无考试”是反对在教学中运用数学史的现实理由[8].考试的压力使得多数教师将教学局限于技术层面,唯恐数学史挤占了课堂训练的时间.在J教师的HPM教学中,数学史不是摆设,而是改进教学的工具.实践表明,数学史的融入促进了学生的学习,最终也提高他们的学习成绩.因此,J教师的教学摆脱了应试的藩篱,实现了一种超越.
·一座桥梁.在J教师的课堂上,学生为萨默斯隧道的神奇而惊叹,为泰勒斯的智巧而称奇,为希帕索斯追求真理的执着而震撼,为阿基米德的海边奇思而顿悟,为赵爽的“负薪余日、聊观周髀”而感动……J教师的教学已经在数学和人文之间架起了一座美丽的桥梁.美国学者Bidwell曾说过:“在教学中融入数学史,可以将学生从数学的孤岛上挽救出来,并将他们安置于一个生机勃勃的新大陆上,这个新大陆包含了开放的、生动活泼的、充满人情味的并且总是饶有趣味的数学.”[9]J教师的HPM实践印证了这一断言.
·一个视角.数学概念的教学设计多种多样,并无定式.但数学史视角关注知识的自然发生过程,从学生认知基础出发,创造学生的学习动机.HPM介入教学后,J教师不再“吝惜”概念引入的时间,而常常采用发生教学法,追求自然无痕的境界,学生们在课堂里获得了如沐春风般的愉悦感.J教师的实践印证了英国教育家斯宾塞(H. Spencer)的断言:“一般教起来使人觉得枯燥甚至讨厌的知识部门,依照自然的方法就成为极其有趣和非常有益的.”[10]
J教师在“中学课堂增值行动专题论坛”上的演讲“融入数学史,激发火热思考”荣获一等奖.如今,她的一些HPM 案例已经成为所任教学校的范例,她的教学风格也引起越来越多人的关注.
4.2 对学生的认知规律有更深的理解
历史发生原理表明,学生对数学概念的理解过程与数学概念的历史发展过程具有一定的相似性.HPM 先驱者、美国数学史家卡约黎(F. Cajori)曾指出:“学生所遭遇的困难往往是相关学科的创建者经过长期思索和探讨后所克服的实际困难.”[11]而史密斯(D. E. Smith)则认为[12]:“困扰世界的东西也会困扰儿童,世界克服其困难的方式提示我们,儿童在其发展过程中会以类似的方式来克服类似的困难.”M·克莱因的观点与卡约黎和史密斯一脉相承:历史上数学家所遇到的困难,正是学生也会遇到的学习障碍[13~14],因而历史顺序是教学的指南[15].因此,参照一个数学概念(公式、定理或思想方法)的历史,就可以预测学生对该概念(公式、定理或思想方法)的理解过程,从而实施符合学生认知发展规律的教学.HPM介入教学后,J教师经常会在教学中参照历史这面镜子,以历史指导自己的教学.她在“课堂增值行动”案例中写道:
比利时—美国科学史家萨顿(G. Sarton)说得好:“历史表明,一种工具的采用几乎在每一种情形下都是极其缓慢的.”“用字母表示数”的历史横跨两千多年,直到16世纪末,法国数学家韦达(F. Viète)才首次用字母来表示任意数.历史启示人们:学生对这一思想的理解必定是一个缓慢的过程,在后续的教学中要慢慢体会,绝不能一蹴而就.只有让学生明白这一点,他们才会有信心把它学好,并充满期待.
以史为鉴,J教师对学生在学习过程中所出现的错误也有了更深刻的理解.
4.3 批判教材的能力得到了提升
随着研究的深入,J教师从HPM的视角来审视教材,批判能力也得到了提高.以下是她对教材中的全等三角形判定定理的思考.
数学课本上给出了“边角边”、“角边角”、“角角边”和“边边边”4种判定方法,其中对“边角边”、“角边角”的证明是用叠置法进行的,而“边边边”则未经证明直接作为定理给出,只在注释中说明:将在以后补上关于“三边对应相等的两个三角形全等”的说理.翻阅教参,发现在该节课的“注意事项”中有这样的说法:“边边边”判定方法,教材是直接给出的,在八年级第一学期将对它进行证明.但事实上,教材利用拼接和等腰三角形知识,只对直角三角形全等作了证明,并未进一步说明“边边边”定理.实际上,用拼接和等腰三角形知识说明“边边边”的方法,根本不用等到八年级,按照课本的体例安排,只要学完等腰三角形的知识,在七年级上学期就马上可以说明了.
数学史上,公元前 1世纪拜占庭数学家菲罗(Philo)就已经用拼接法证明了“边边边”定理:移动其中的一个三角形,使其一边与另一个三角形的对应边重合,而该边所对顶点与另一三角形的对应顶点位于它的两侧,联结这两个顶点,得到两个等腰三角形,故重合边所对的角相等,于是根据“边角边”定理,两个三角形全等.可见,如果掌握数学史知识,就可以在较短时间内让全等三角形知识形成系统,使学生“知其然又知其所以然”.数学史的教育价值由此可见一斑!
J教师在设计全等三角形和等腰三角形这部分知识时,对课本的体例作了改动:在讲解完“边角边”、“角边角”、“角角边”这3个定理,就以例题课的形式讲解了等腰三角形定理及欧几里得的证明.以此为铺垫,“边边边”定理的拼接证明也就水到渠成了.
4.4 拓展课本知识的意识得到了增强
用历史的眼光审视教材,J教师常发现其中的不足之处,于是,就常常拓展一些有利于学生理解、体现知识应用、引人入胜的内容.“全等三角形的应用”就是其中一例.
从历史上看,全等三角形和相似三角形一样,也源于测量.但教材有相似三角形的应用,却无全等三角形的应用,对两个知识点的处理并不一致.J教师对全等三角形知识作了拓展,结合数学史,增加了一节全等三角形应用课.
首先用“拿破仑遇河”的故事作为情境,引入课题:拿破仑军队在行军途中为一湍急的河流所阻,为架浮桥,亟需测出河的宽度.如何测河宽?这位叱咤风云的法国将军急得团团转.同学们能帮他想想办法吗?J教师提示:可用全等三角形知识来解决.学生想出了各种各样的测量方法,其中一位学生借助角边角定理来解决,与古希腊泰勒斯的方法如出一辙,而且恰恰也是拿破仑的一名随军工程师想出的方法!但由于没有学过立体几何,这位学生刻画得不够清晰,班里的其他学生对此不甚了了.此时,J教师介绍泰勒斯及其测量方法,并取出课前制作好的教具,让那名学生上台演示,于是,古人的方法清晰而生动地再现于课堂.接着,J教师让学生进一步设计其它的方案.基于泰勒斯方法的引领,学生不断提出各种新方法.最后,J教师通过3个例子进一步讲解全等三角形在测量上的应用.
对学生的问卷调查和对师生的访谈都表明,这样的拓展课非常成功,受到师生一致的好评.一位观摩J教师“全等三角形应用”课的教师如是说:“如果所有的课都能以这种形式来上,那么学生一定都会喜欢数学课.”一位学生受访时表示,希望学校每周都能开设一次这样的拓展课.
4.5 教学研究能力得到了提高
经过两年的行动研究,J教师的教学研究能力有了很大的提高.在《数学教学》上发表了一篇HPM教学论文,并在上海市教学论文评比中获奖;另一篇论文也在投稿之中.
2011年5月,在华东师范大学主办的第四届“数学史与数学教育国际研讨会”上,J教师作了“数学史融入初中数学教学的行动研究”的学术报告,获得与会者的好评.自此,J教师不定期与大学数学教育研究者、研究生以及具有共同爱好的中学数学教师聚会,讨论初中数学中的数学史以及HPM视角下的数学教学设计,J教师如今已经成为国内HPM学术共同体的一员.
J教师在HPM教学实践中,充分感受到了数学史的无穷价值,但也深深感受到HPM教学的艰难,她在教学反思中写道:“数学史功底的薄弱是一线教师充分发挥数学史教育功能的最大障碍.”HPM让她认识到自己在历史知识上的欠缺,时时激励她不断学习、不断进步.
5 结 语
J教师的经历表明,HPM可以有效地促进中学数学教师的专业发展.因此,在教师培训中,有必要加强数学史的教学.不是泛泛讲授数学的通史,而是挖掘中学数学中各个知识点背后的历史;不仅讲授历史,而且讲授如何将数学史用于课堂教学设计.这样,数学史才会引起数学教师的兴趣.
另一方面,研究者可以先开发若干成功的HPM教学案例,并将其推广,使广大一线教师看到数学史融入数学教学的真实效果.这样,必有更多的中学数学教师走进HPM领域.J教师让研究者看到,中学教师完全能够进入HPM学术共同体.
要让HPM从书斋真正走进中学课堂,还应加强大学研究者与中学一线数学教师之间的合作,前者进行深入的教育取向的数学史研究,同时引领后者进入数学史的诠释学循环;后者根据自己的诠释,选取适合课堂教学的历史材料,然后将数学史的诠释学循环与原有的数学教学诠释学循环融合起来,设计并实施课堂教学.J教师的专业成长表明,这种合作富有成效,前景广阔,令人期待.
致谢:文章曾在东亚四国“通过课例研究提高数学与科学教师教学能力”国际会议(2012年1月26日—28日,广岛)上宣读,投稿时做过部分删改.作者对广岛大学教育学研究科教育学部的资助表示感谢!
[1]Fauvel J. Using History in Mathematics Education [J]. For the Learning of Mathematics, 1991, 11(2): 3-6.
[2]Tzanakis C, Arcavi A. Integrating History of Mathematics in the Classroom: An Analytic Survey [A]. In: Fauvel J, van Maanen J. History in Mathematics Education [C]. Dordrecht: Kluwer Academic Publishers, 2000.
[3]Jankvist U T. A Categorization of the “Whys” and “Hows” of Using History in Mathematics Education [J]. Educational Studies in Mathematics, 2009, 71(3): 235-261.
[4]Jahnke H N. The Historical Dimension of Mathematics Understanding-objectifying the Subjective [R]. Proceedings of the 18th PME, Lisbon: University of Lisbon, 1994.
[5]洪万生.PCK vs. HPM:以两位高中数学教师为例[D].香港教育学院,2005.
[6]苏意雯.数学教师以 HPM 促进专业发展之个案研究[R].数理教师专业发展学术研讨会,彰化:国立彰化师范大学,2004.
[7]苏意雯.运用古文本于数学教学——以开方法为例[J].台湾数学教师电子期刊,2007,(9):56-67.
[8]Fauvel J, van Maanen J. History in Mathematics Education [M]. Dordrecht: Kluwer Academic Publishers, 2000.
[9]Bidwell J K. Humanize Your Classroom with the History of Mathematics [J]. Mathematics Teacher, 1993, 86 (6):461-464.
[10]Spencer H. Education: Intellectual, Moral, & Physical [M]. New York: Hurst & Company, 1862.
[11]Cajori F. The Pedagogic Value of the History of Physics [J]. The School Review, 1899, 7(5): 278-285.
[12]Smith D E.. Teaching of Elementary Mathematics [M]. New York: The Macmillan Company, 1900.
[13]Kline M. A proposal for the High School Mathematics Curriculum [J]. Mathematics Teacher, 1966, 59 (4): 322-330.
[14]Kline M. Logic Versus Pedagogy [J]. American Mathematical Monthly, 1970, 77 (3): 264-282.
[15]Albers D J, Alexanderson G L. Mathematical People: Profiles and Interview [M]. Boston: Birkhäuser, 1985.
