融合邻域模型与隐语义模型的推荐算法

鲁权，王如龙，张锦，丁怡

湖南大学信息科学与工程学院，长沙 410082

融合邻域模型与隐语义模型的推荐算法

鲁权，王如龙，张锦，丁怡

湖南大学信息科学与工程学院，长沙 410082

1 引言

随着互联网的普及与电子商务的快速发展，信息的过度膨胀[1]与冗余导致人们在寻找自己所需的信息时花费大量时间。个性化推荐系统[2]能够提供一种有效的机制，帮助用户在缩减信息获取过程耗费的时间代价的同时保证信息获取的质量，因而得到越来越多研究者的关注。

协同过滤[3]是目前各个推荐系统中应用最为广泛和成功的技术，它的基本思想是，如果两个或多个用户在某些信息（例如网页或者商品）的选择上表现出相同的兴趣或给出接近的评价，那么在其他一些信息的选择上也可能做出相同的选择或给出接近的评价。为了构建推荐系统，协同过滤算法需要对用户和物品因素进行比较，两种主流的方法分别是邻域模型和隐语义模型。

邻域模型[4]主要刻画物品或者用户之间的相似度。一个基于物品的邻域模型通过计算用户对相似物品的评分来预测用户对该物品的评分。这种方法不需要比较用户与物品之间的关系，只需要关注物品之间的相似度就能做出计算。

隐语义模型[5]，例如奇异值分解（Singular Value Decomposition，SVD）[6]的基本思想是把高维向量空间模型[7]中的文档映射到低维的潜在语义空间中。降维处理使得物品与用户的潜在关系能够在潜在子空间中自然的显现出来，通过主成分分析[8]对原有数据进行简化的同时，去除噪音和冗余，揭示隐含在复杂数据背后的简单结构。

传统的协同过滤算法一般采用评分这一显性反馈[9]——项目评价矩阵进行相似度计算，然而随着电子商务系统规模的增长，协同过滤算法面临着两个巨大挑战，即数据稀疏性[10]、可扩展性[11]，而隐性反馈[12]如用户的浏览记录和页面点击行为数据量更大，可以弥补因为显性反馈数据缺少带来的不足。

本文将邻域模型和隐语义模型结合，提出一种新的融合显性与隐性反馈的协同过滤算法模型，称为（Hybrid-SVD Model）。该模型能有效地将两种反馈信息结合起来，并综合考虑用户与物品之间隐含关系。实验数据表明Hybrid-SVD Model在Netflix数据集上性能优于已有的算法。

2 融合邻域模型与隐语义模型的协同过滤推荐算法

协同过滤算法需要数值形式的评分来进行预测。虽然显性反馈满足这个要求，但是显性反馈评分数量通常不足以训练出准确的模型。另一方面，隐性反馈因为不需要额外的评分操作，在数量上比显性反馈大很多。如果找出一种方法能够有效地将隐性反馈信息转化为适合的数值形式的估计值，就能够提高使用显性反馈信息训练的模型准确性。对于Netflix数据集，最自然的隐性反馈信息当然是电影的租借历史信息，然而该信息未能公开。另一个隐性反馈信息则是用户的历史评分行为信息，这一隐性反馈信息表明用户偏好选择某些电影进行评分（不管评分高或者低）。虽然这一隐性反馈信息不如其他隐性反馈信息广泛或者独立，但是在一般基于评分的推荐系统中普遍存在，并且能够显著地提高预测精度。

需要提出的是，本文提出的算法并不只针对这一特定的隐性反馈信息，为了保证一般性，每个用户u与物品i构成两个数据集：显性反馈数据集R，包含用户对物品的显性评分信息；隐性反馈数据集N(u)，包含所有用户对物品的隐性偏好数据。

2.1 融合隐性反馈的邻域模型

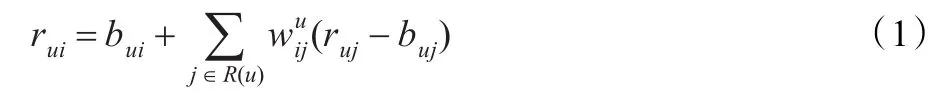
加入偏置项bui=μ+bu+bi，这是考虑在实际情况下，一个评分系统有些固有属性和用户物品无关，而用户也有些属性和物品无关，物品也有些属性和用户无关。因此，μ为训练集中所有记录的评分的全局平均数，表示网站本身对用户评分的影响。bu为用户偏置项，表示在用户评分习惯中和物品无关的因素，如有些用户偏苛刻，普遍评分较低而有些用户比较宽容，评分偏高。bi为物品偏置项，表示物品接受评分中和用户无关的因素，例如物品本身质量

首先考虑基于邻域的协同过滤模型，模型为如下形式：很高，因此获得评分普遍比较高。{|j∈R(u)}为给定的物品i在给定的显性反馈集R(u)中的插值权重。

利用隐性反馈信息，添加另外一组权重，可将公式（1）改写为如下形式：

cij与wij类似，对于两个物品i和j，一个用户u对物品j的正隐性反馈信息会在模型中修正预测值rui，给出一个更高的预测值。将这些权值视为全局偏移量，而非基于用户或者基于项目的系数，便强化了缺失评分值的影响，即用户的预测评分不仅与其评分历史数据相关，同时与他未评分的物品相关，特别是那些相对热门，而用户并未评分的物品。例如，假设一个电影评分数据集显示那些对“指环王3”评分较高的用户通常对“指环王1－2”的评分也相对较高，这就使得“指环王3”与“指环王1－2”之间有很高的权值。假设一个用户没有对“指环王1－2”进行评分，那么他对“指环王3”的预测评分会变低，因为相应的权值cij在模型中为0。

2.2 考虑邻域影响的隐语义模型

本文工作的一个重要目标是设计一种融合邻域模型与隐语义模型的改进协同过滤模型。从抽象的层次来看，协同过滤可以看做矩阵填充（Matrix Completion）问题：用户对商品的评分组成一个评分矩阵，每个用户可能仅对其中一小部分商品做过评价，因此这个矩阵通常是非常稀疏的。对于如何补全一个矩阵，历史上有过很多研究。一个空的矩阵有很多种补全方法，这里需要找出一种对矩阵扰动最小的补全方法。一般认为，如果补全后矩阵的特征值和补全之前矩阵的特征值相差不大，则称其扰动小。因此，最早的矩阵分解模型是从数学上的SVD（奇异值分解）开始的。然而传统的SVD分解需要用一个简单的方法补全稀疏评分矩阵，评分矩阵会变成一个稠密矩阵，从而使评分矩阵的存储需要非常大的空间，这种空间需求在实际系统中时不太可接受的。同时分解算法时间复杂度也很高，特别是在稠密的大规模矩阵中非常慢。正是由于上面的两个缺点，SVD分解算法提出后在推荐系统领域并未得到广泛关注，直到2006年Netflix Prize开始后，Simon Funk公布了一个算法（Funk-SVD）。从矩阵分解[13]的角度，将每一个用户u关联一个用户因子向量pu∈Rf，将每一个物品i关联一个物品因子向量qi∈Rf。如果将评分矩阵R分解为两个低维矩阵相乘：

要最小化上面的损失函数，可以利用随机梯度下降法（Stochastic Gradient Descent）[14]。该算法是最优化理论里基础的优化算法，它首先通过求参数的偏导数找到最速下降的方向，然后通过迭代法不断地优化参数。

上文定义的损失函数里有两组参数（puf和qif），最速下降法需要首先对它们分别求偏导数，可以得到：

然后，根据随机梯度下降法，需要将参数沿最速下降方向向前推进，因此可以得到如下递推公式：

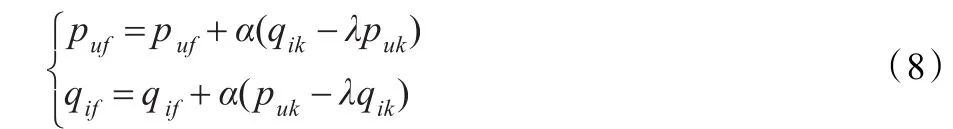
其中，α是学习速率（Learning Rate），它的取值需要通过反复实验获得。

初始化P、Q矩阵的方法很多，一般是将这两个矩阵用小范围随机数填充，根据多次实验表明，随机数需要和1/sqrt(F)成正比。

由于特征向量维数f固定，因此预测的时间复杂度仅为O（1）。在用梯度方法对当前单个特征向量元素求偏导时，和其余特征向量相关的项均为0，因此回避了一般SVD算法中需要迭代或插值求解矩阵中未知元素的问题。另外也可以看出，每次迭代使用一个评分数据，整个训练过程只需要存储特征向量的内存空间，因此特别适合于有非常大数据集的情况。

这种算法每次迭代更新只需要很少的计算量，求解每个特征向量都是相同的时间。和批处理矩阵分解相比，数据量的多少并不影响更新计算速度。算法每次产生一个特征向量，并且保证该向量是目前为止最显著的特征向量。这意味着每次从矩阵中提取出来的都是最重要的特征，保证了算法的精度。与其他增量方法相比，这种学习方法区别在于前者收敛于整个数据集的特征值分解，而不是目前所见数据为止的一个最优解[15]。

将矩阵分解模型融合隐形反馈信息进行扩展，将评分预测公式改写为：

根据随机梯度下降法，得递推公式：

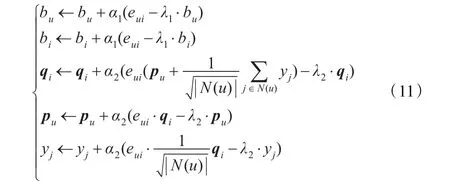
其中eui=rui-即真实评分与预测评分的差值。

从公式（11）可以看出，当|N(u)|数量较大时，即隐性反馈信息较多时，隐性反馈信息在评分预测中占主要因素；当|R(u)|数量较大时，即显性反馈信息较多时，显性反馈信息在评分预测中占主要因素。一个显性信息通常要比一个隐性反馈信息有价值。而如何平衡这两个信息的权重，则是由相关参数xj与yj在模型的迭代学习中自动获得的。

改进后的模型有效融合了隐性反馈信息。通过融合隐性反馈信息，提供了额外的用户偏好信息，从而改进了算法的精度。隐性反馈信息的作用，在那些提供隐性反馈信息远高于显性反馈信息的用户体现得更为明显。

3 实验结果及评估

3.1 Netflix数据集

本文对算法的评估基于Netflix数据集，其中包括了从1998年10月到2007年8月的超过1 900 000 000个评分，这些评分来自于11 700 000多个用户对85 000多部电影的1～5之间的评分，评分高则表示用户喜欢这部电影。为了测试各种不同的算法，Netflix提供了两个测试数据集。一个是探测集（Probe Set），这个集合在原1亿条训练数据集中抽取140万条评分数据，因此在这个集合中，用户对电影的真实评分是知道的。

另一个是测验集（Qualifying Set），测验集由280万条数据组成，但是没有提供电影评分的真实数据。两个数据集都挑选了一些难以预测的用户，让人们对他们的评分进行猜测。使用均方根误差（RMSE）作为性能评估的标准，定义如下。

对于测试集中的一对用户和物品(u，i)，用户u对物品i的真实评分是rui，而推荐算法预测的用户u对物品i的评分为，那么一般可以用RMSE度量预测的精度：

在对模型进行训练之前，将探测集从训练集中剥离，在剩下的数据集上训练出来的模型在探测集上进行预测评估。

实验表明，如果包含探测集来训练，最后得到的RMSE将比没有包含探测集得到的结果降低0.03左右，这是一个很大的提高。因此，这种剥离探测集训练模型的方法将更接近真实预测情况。

3.2 结果与讨论

本文通过实验对比Hybrid-SVD算法在评分预测问题中的性能。在该算法中，重要的参数有3个：隐特征的个数k、学习速率alpha和正则化参数lambda。通过实验发现，隐特征个数k对算法性能影响最大。因此，固定学习速率alpha与正则化参数lambda，研究隐特征个数k对推荐结果性能的影响。算法参数选择：学习速率参数alpha与正则化参数lambda通过交叉验证决定。

本文采用alpha=0.007，lambda1=0.005，lambda2=0.015进行实验。在训练集上迭代次数选用15次。学习速率参数按每次迭代缩减为0.9倍的速度递减。控制邻域范围的参数，即隐特征个数k，通过实验证明k值越大，实验精度越高，因此需要在算法精度与计算代价之间取得平衡。

在Netflix数据集上采用新邻域模型的实验结果如图1所示。采用不同数值的参数k进行模型学习。从蓝色曲线中可以看出算法精度随着k值的增加单调上升，当k值从250上升到无穷（对于该数据集，无穷代表全部电影项，即k=17 770）时，RMSE从0.913 9下降至0.900 2。将隐性反馈信息从该模型剔除后重复进行实验，结果如红色曲线所示，可见算法精度明显低于融合隐性反馈信息的模型，并且，随着k值增加，这种精度差别更加明显，即没有融合隐性反馈信息的模型，算法精度随k值增加提升不如融合隐性反馈的模型明显。

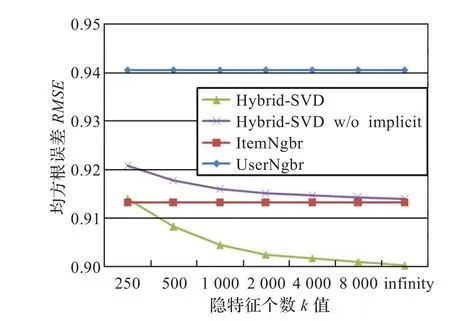
图1 不同k值各模型在Netflix数据集下测试的RMSE值

作为对比，本文提供了两种典型的基于邻域的模型，即基于用户的邻域模型（UserNgbr）和基于物品的邻域模型（ItemNgbr）。对于每种模型，选用优化的参数，对基于用户的邻域模型，选用邻居大小为20，而对于基于物品的邻域模型，选用邻居大小为50。实验结果如图1两条曲线所示，这里k值对以上两模型没有影响。由实验数据可以得出基于用户的邻域模型算法精度要略低于基于物品的邻域模型。另外，从图中还可以看出，曲线对应几个特征向量的RMSE下降开始很快，而随着k值的增加下降速度明显变缓，这也从侧面印证了算法每次计算出的都是最显著的特征向量。

其次考虑学习速率alpha对算法性能的影响。采用固定隐特征个数k=40，正则化参数lambda为0.025时，算法获得的预测误差如表1所示，学习速率alpha从0.004降低到0.000 5的过程中，算法的均方根误差RMSE从0.923 7降低至0.911 9，但同时迭代次数从47次增加至361次，这表明更小的学习率可以产生更低的预测误差，但同时算法的收敛速度也变得更慢。如何平衡学习速率和算法效率之间的关系，需要选择一个合适的速率值。

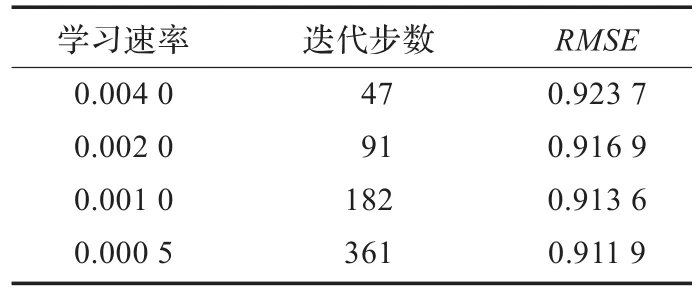
表1 固定隐特征个数k=40，正则化参数lambda为0.025时算法获得的预测误差

最后，在算法性能方面，本文模型需要进行预运算来估计各个参数，而单个评分的实时预测则可在0.1 ms之内完成。与运算耗费时间随k值增加而上升，每次迭代耗费的运行时间如图2所示，使用Intel酷睿E2160 CPU，4 GB RAM的普通PC进行运算。

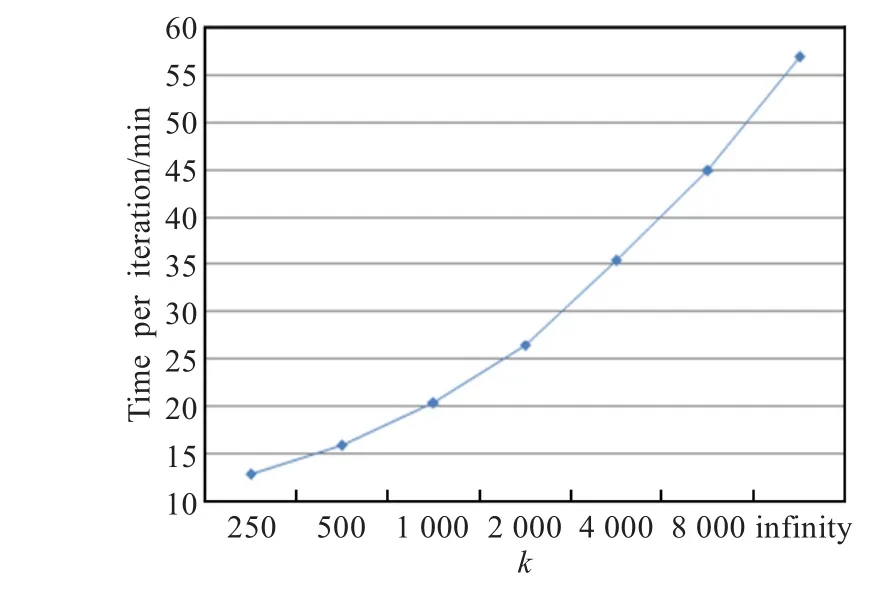
图2 新模型在不同k值下每次迭代所需时间

运算结果表明，算法在保持较高准确度的前提下，仍具有良好的性能。

4 总结

通过融合显性反馈和隐性反馈信息改进了推荐算法。实验数据评估结果表明，本文采用的基于Netflix数据集中的隐性反馈信息在比较有限的情况下，算法的精度仍然得到显著提高，其性能特性比较适合处理大规模数据集。

[1]Bawden D，Robinson L.The dark side of information：overload，anxiety and other paradoxes and pathologies[J].Journal of Information Science，2009，35（2）：180-191.

[2]Sarwar B，Karypis G，Konstan J，et al.Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web，2001：285-295.

[3]Su X，Khoshgoftaar T M.A survey of collaborative filtering techniques[J].Advances in Artificial Intelligence，2009，32（4）：95-101.

[4]Linden G，Smith B，York J.Amazon.com recommen-dations item-to-item collaborative filtering[J].IEEE Internet Computing，2003，7（1）：76-80.

[5]Hoff P D.Multiplicative latent factor models for description and prediction of social networks[J].Computational and Mathematical Organization Theory，2009，15（4）：261-272.

[6]Sarwar B，Karypis G，Konstan J，et al.Item-based collaborative filteringrecommendationalgorithms[C]//Proceedingsofthe 10th International Conference on World Wide Web ACM，2001：285-295.

[7]Dumais S T.Latent semantic analysis[J].Annual Review of Information Science and Technology，2004，38（1）：188-230.

[8]Abdi H，Williams L J，Valentin D，et al.STATIS and DISTATIS：optimum multitable principal component analysis and three way metric multidimensional scaling[J].Wiley Interdisciplinary Reviews：Computational Statistics，2012，4（2）：124-167.

[9]Hu Y，Koren Y，Volinsky C.Collaborative filtering for implicit feedback datasets[C]//Proceedings of the 8th IEEE International Conference on Data Mining（ICDM’08）.[S.l.]：IEEE，2008：263-272.

[10]曾小波，魏祖宽，金在弘.协同过滤系统的矩阵稀疏性问题的研究[J].计算机应用，2010，30（4）：1079-1082.

[11]Su X，Khoshgoftaar T M.A survey of collaborative filtering techniques[J].Advances in Artificial Intelligence，2009（4）.

[12]Koren Y.Factorization meets the neighborhood：a multifaceted collaborativefilteringmodel[C]//Proceedingsofthe14th ACMSIGKDDInternationalConferenceonKnowledge Discovery and Data Mining.[S.l.]：ACM，2008：426-434.

[13]Koren Y，Bell R，Volinsky C.Matrix factorization techniques for recommender systems[J].Computer，2009，42（8）：30-37.

[14]Koren Y.Factor in the neighbors：Scalable and accurate collaborative filtering[J].ACM Transactions on Knowledge Discovery from Data（TKDD），2010，4（1）：1-11.

[15]顾晔，吕红兵.改进的增量奇异值分解协同过滤算法[J].计算机工程与应用，2011，47（11）：152-154.

LU Quan,WANG Rulong,ZHANG Jin,DING Yi

School of Information Science and Engineering,Hunan University,Changsha 410082,China

As one of the most successful approaches to building recommender systems,Collaborative Filtering（CF）uses the known preferences of a group of users to make recommendations or predictions of the unknown preferences for other users.The two successful approaches to CF are latent factor models,which directly profile both users and products,and neighborhood models, which analyze similarities between products or users.This paper introduces some innovations to both approaches.The factor and neighborhood models can now be smoothly merged,thereby building a more accurate combined model.Further accuracy improvements are achieved by extending the models to exploit both explicit and implicit feedback by the users.The methods are tested on the Netflix data,and the results are better than those previously published on that dataset.

recommender systems;Collaborative Filtering（CF）;latent factor model;Root Mean Square Error（RMSE）

作为目前构建推荐系统最成功的方法之一，协同过滤算法（CF）是利用已知的一组用户喜好数据来预测用户对其他物品的喜好从而做出个性化推荐的。两种比较成功的协同过滤算法能够直接刻画用户和物品因子的隐语义模型，以及分析物品或者用户之间相似度的邻域模型。提出了一种针对这两种模型的改进方法，使得隐语义模型和邻域模型能够有效结合，从而构建出一个更精确的融合模型。在融合用户的显性反馈与隐性反馈信息对模型进行扩展后，又使得精确度进一步提升。在Netflix数据集上进行测试，实验结果表明，该融合算法在Netflix数据集上的性能优于其他算法。

推荐系统；协同过滤；隐语义模型；均方根误差

A

TP391

10.3778/j.issn.1002-8331.1303-0357

LU Quan,WANG Rulong,ZHANG Jin,et al.Recommender algorithm combined with neighborhood model and LFM. Computer Engineering and Applications,2013,49（19）：100-103.

国家科技支撑计划项目（No.2012BAF12B20）；国家自然科学基金（No.60901080）。

鲁权（1986—），男，硕士研究生，研究领域为数据挖掘，机器学习；王如龙（1954—），男，教授，硕士生导师，研究方向为企业信息化，软件工程，IT项目管理；张锦（1979—），通讯作者，男，博士，副教授，研究方向为软件工程，IT项目管理，人工智能，服务科学；丁怡（1987—），女，硕士研究生，研究方向为物流信息技术，企业信息化。E-mail：mail_zhangjin@163.com

2013-03-25

2013-05-20

1002-8331（2013）19-0100-04

CNKI出版日期：2013-06-08http://www.cnki.net/kcms/detail/11.2127.TP.20130608.1001.024.html