并行分区拣货系统储位优化设计

李晓春，钟雪灵，王雄志，王国庆

1.华南师范大学南海校区信息工程与技术系，广东南海 528225

2.广东金融学院计算机系，广州 510520

3.华南农业大学经济管理学院，广州 510642

4.暨南大学管理学院，广州 510632

并行分区拣货系统储位优化设计

李晓春1，钟雪灵2，王雄志3，王国庆4

1.华南师范大学南海校区信息工程与技术系，广东南海 528225

2.广东金融学院计算机系，广州 510520

3.华南农业大学经济管理学院，广州 510642

4.暨南大学管理学院，广州 510632

1 引言

零售型配送中心由于订单多为多货品小批量型，大约80%的订单货品都少于一个整货箱，需要进行拆箱拣货。这类配送中心经常通过分区拣货方式跨越好几个仓储区完成订单拣货任务。所谓并行分区（如图1所示）就是将拣货员分配到各个拣货区，即将整个拣货区分成几块，由一个或一组固定的拣货员负责拣选某区域内的货品，在有订单需求时，结合批量拣货方式及订单分割策略进行拣货。其中，批量拣货是指拣货员以批量作业的形式同时拣取一组订单品项的作业方式，该系统中，将一组订单首先按区域进行订单的分割，各个拣货区根据分割后的子订单同时进行拣货作业，直到所有分区拣货作业完成品项汇总为止。系统中，由于各分区拣货员拣货速度不同，工作负载若不均衡，经常造成部分分区拣货员忙碌和部分分区拣货员空闲的情况，导致瓶颈现象、阻塞现象及员工效率降低等。

目前，对并行分区拣货作业的研究大都首先通过历史订单数据计算品项需求之间的相似关系（即，某两种品项的需求经常发生在同一张订单的概率，下文统一称为“相似性系数”）[1-2]，然后基于同类族模型思想[3]建立自然族（Natural Cluster）模型，并提出启发式算法求解使订单需求的所有品项均衡存储在不同的分区中，但忽略品项在各分区的货位分布，在各分区内品项采用随机存储策略。文献[4]对常见的拣货策略做了综述；文献[5-9]则通过模拟实验，从不同角度模拟测试了巷道布局、存储策略及分区规则不同时的拣货效率及巷道的最优布局；文献[10]主要考虑了动态分区拣货策略，提出“排序-动态-平衡”思想，提高拣货效率；文献[11-14]则重点考虑了分区拣选策略在自动分拣机上的应用及优化；文献[15]考虑被拣货物具有一定质量和体积的实际，提出了当量订购次数的概念及系统利用率评价函数。但多数算法在设计中未考虑各分区中拣货员拣货速度之间的差异，实际拣货中不仅因各分区中待拣选品项间的差异，而且因拣货员拣货速度的不同，导致各分区工作时间不均衡。

鉴于此，本文考虑各分区拣货员拣货速度不同的情况下，对并行分区拣货系统优化的目的为：（1）同一订单中经常出现的品项尽可能分布在不同的分区中，避免部分分区出现无任务作业的情况；（2）分区中根据拣货员的速度，安排较多品项给拣货快的分区，较少品项给拣货慢的分区，从而均衡各分区的作业时间。其作业流程如图1[16]所示。

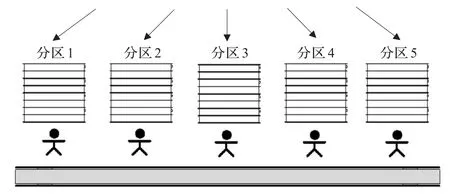
图1 并行分区拣货系统示意图

2 储位策略优化模型

设拣货系统中，拣货员分布于Z个独立的分区，同样，品项也被分到该Z个独立的分区中，各分区间无缓冲区（或缓冲设备）。

假设1拣货区按照从左到右的方向依次排列，分别设为z=1，2，…，Z，对于该定一组订单，各分区拣货员同时从领单点处领取其负责的分区内的任务，同时开始拣货。即将订单进行分割，使所有拣货员同时作业。

该假设主要是基于拣货区一般是根据品项在配送中心的流向（如集货点的位置）布置。

假设2每一订单需要不同种类的品项，且每种品项需求数量较小，均为小型品项，各种品项都可在一个拣取动作中完成，即每种品项需求数大于1时，视为一个品项，可一次拣选完成。

假设3整个拣货线上拣货员的速度恒定且不同，拣货员的行走速度与拣取速度一起并入拣货速度中，其速度为νz，表示单位时间内拣货员z可拣选品项的数量，1≤z≤Z。用tz表示拣货员z拣选每一品项所需要的时间，即tz=1/νz。

假设4一个拣货动作只拣取一种品项，每次拣货清单不会超过拣货车载容积限制。

假设5品项是由订单中挑选出来进行聚类群摆放到各个分区中，各分区的储位不一定能摆满品项。品项储存位置唯一，品项储位一经摆放，在相对长一段拣货周期内都不会改变；且不允许缺货发生。

根据假设，每一品项不论其出现在一张订单还是多张订单中，其均为独立拣选，且每种品项的拣选次数等于该品项在不同订单中出现的总次数。拣货员在某订单上花费的拣货时间与该订单在拣货员所负责分区的品项种类有关。显然，如果订单需求的所有品项在不同分区中的分布可使得各分区拣货作业时间趋于相同，则拣货员的空闲时间将减少。但是订单需求品项种类一般不同，各订单在各分区的品项需求不同，数量也存在差异，且拣货员的拣货速度不同，从而导致品项均衡储存的复杂性。因此，目标函数用数学模型表示为：

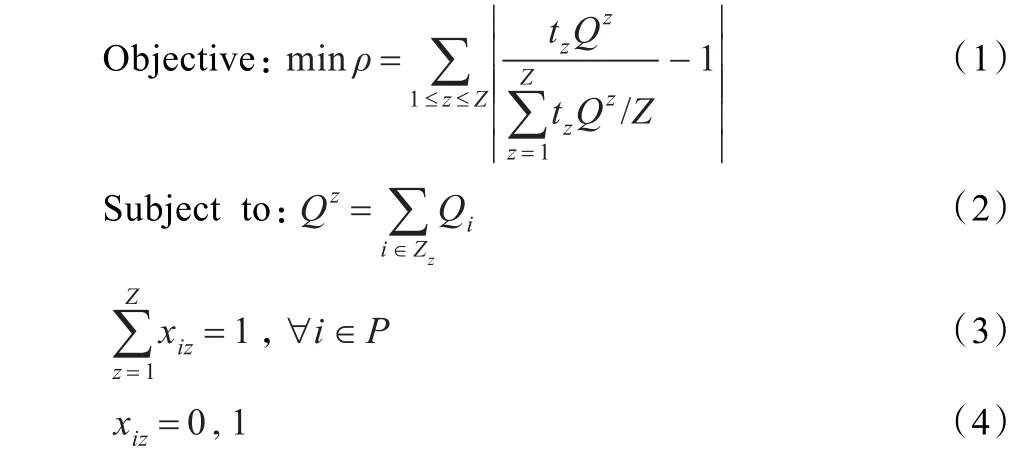
其中，式（1）为目标函数，式（2）表示拣货员z的拣货工作任务量，式（3）保证每一品项只能存放于一个分区中，式（4）为0-1决策变量。

模型中涉及的参数如下所示。

Z：拣货区分区总数；n：拣货区总品项数量；P：品项集，P={1，2，…，n}；O：订单集；Qi：品项i在历史订单数据库中的总需求次数；Q：配送中心拣货员在历史订单数据库中总拣货次数；Nz：分区z中的所有品项集，Nz={n1，n2，…，nPz}；tz：拣货员z拣选每一品项平均所需时间；：拣货员z所用的总拣货时间；：各分区平均拣货时间；ρz：拣货员z的总拣货时间占各分区平均拣货时间的比例；ρ：误工率，即每个拣货员完成其分区拣货任务的时间的差异率之和；xiz：为储位均衡指派方案的0-1变量，品项i被分配到第z个分区中，则xiz=1，否则xiz=0。

当拣货员拣货速度相同时，均衡分配各分区的作业量已为NP-难问题，无法获得时间复杂度为问题规模的多项式时间精确算法，故只有寻找时间复杂度较小的近似算法或启发式算法。下面通过分析订单品项间的关系，设计结合品项关联规则的储位指派算法。

3 储位指派算法

设P={1，2，…，n}为所有品项的集合，D为历史订单数据库，O为订单品项子集，O⊆P，每个订单具有唯一的标志Oi，设A是由部分品项构成的集合，称为品项集，简称项集。订单O中包含项集A，当且仅当A⊆O，如果项集A包含了k个品项，则称其为k项集，或称A的长度为k。

定义1品项集A的支持度。历史订单数据库D中，支持品项集A的订单数O称为品项集A的支持数，记为Count(A)。设历史订单数据库D中，总的订单数为|D|，则品项集A的支持度为：Count(A)/|D|，记为S(A)。

在设计品项储位指派算法时，同时希望经常出现在同一张订单中的品项分布在各个分区中，避免部分分区经常出现无作业任务的情况。例如，品项集A中包含品项i和j，其支持度为S(A)，即品项i和j在同一种订单中出现的概率Sij，Sij=S(A)，这里需要把支持度越大的品项储存在不同的分拣区，以使订单中的品项均衡分布在各分区中，从而每个拣货员均有拣选任务，即

下面将根据历史订单库D中的数据，寻找D中所有的频繁关联规则，找出所有频繁项集。所谓频繁关联规则是指这些规则的支持度不低于预先给定的最小支持度，从而得到相应的频繁项集。根据频繁关联规则及拣货员的拣货速度，设计结合品项关联规则的储位指派算法，均衡分派品项在各分区的存放，使订单在各分区的拣货时间均衡。

寻找关联规则，首先根据配送中心拣货系统品项及订单特征，利用Excel试算表产生品项及历史订单数据。然后用基于频繁模式树FP-Tree的关联分类规则挖掘算法FP-growth[17]对品项之间的关系进行挖掘，根据频繁关联规则及拣货员的拣货速度设计储位分配算法。基于FP-tree的关联规则挖掘算法FP-growth是将发现频繁模式的问题转换成递归地发现一些短模式，然后链接后缀。它使用最不频繁的项目做后缀，提供了较好的选择性，可显著降低搜索开销。

频繁模式树FP-tree的构造涉及的参数主要有：FP-tree树中，每个节点由4个域组成，是节点名称node-name、节点计数node-count、节点链指针node-link和父节点指针node-parent。其中，node-name记录节点所表示的品项名，node-count记录该节点所表示品项被拣选的次数，node-link为指向FP-tree中具有相同的node-name值的下一节点，即通过node-link将FP-tree中具有相同node-name值的节点连接起来，node-parent为指向父节点的指针。另外，为了方便树遍历，创建一个频繁项目头表，它由两个域组成：品项名称node-name以及节点链头node-head。其中，node-head为指向FP-tree中具有相同node-name值的首节点的指针。算法具体步骤描述如下：

4 算法性能测试

运用VB语言分别对AHACAR算法及随机存储策略算法编程。设计的大量算例在CPU为Intel Pentium Processor1.70 GHz的PC机上进行模拟运算，测试算法性能。拣货区共有60种品项（SKU），每个订单中的品项种类为5～12种，每种品项的需求量为1～5个。有5个拣货区，由5个拣货员负责，1个拣货员负责1个拣货区。拣货员的拣货速度同上，分别是0.22 min/品项，0.30 min/品项，0.35 min/品项，0.4 min/品项，0.48 min/品项。历史订单数据库由Excel试算表产生每行不重复的介于1～60随机数2 000行，列数介于5～12列，数字1～60分别代表品项P1～P60，从而产生历史订单数据库结果。本算例产生的历史订单数据库中，品项集合为：I={P1，P2，…，P60}，在此分别用数字代替各品项，如用“1”代替“P1”，品项集合可简写为I={1，2，…，60}，其中，任一品项集（itemset）为品项集I的子集合；该数据库由2 000笔订单交易D={O1，O2，…，O2000}所构成，其中，Oi也是由I中任意品项的子集合所形成的交易资料。对数据库资料统计分析后，其最大订单项为12项，最小订单项为7项，总拣货次数为23 016次，由品项出现次数统计可以发现品项出现次数最高为705次，最低的品项113次。各品项的拣选率见表1；订单与订单品项关系图及品项出现次数分别如图2、图3所示。

比较按单拣货和批量拣货两种方式，每次批量作业为5个订单进行合并，并与随机存储策略进行比较。为了评价优化算法的优化程度，定义绩效改进为：

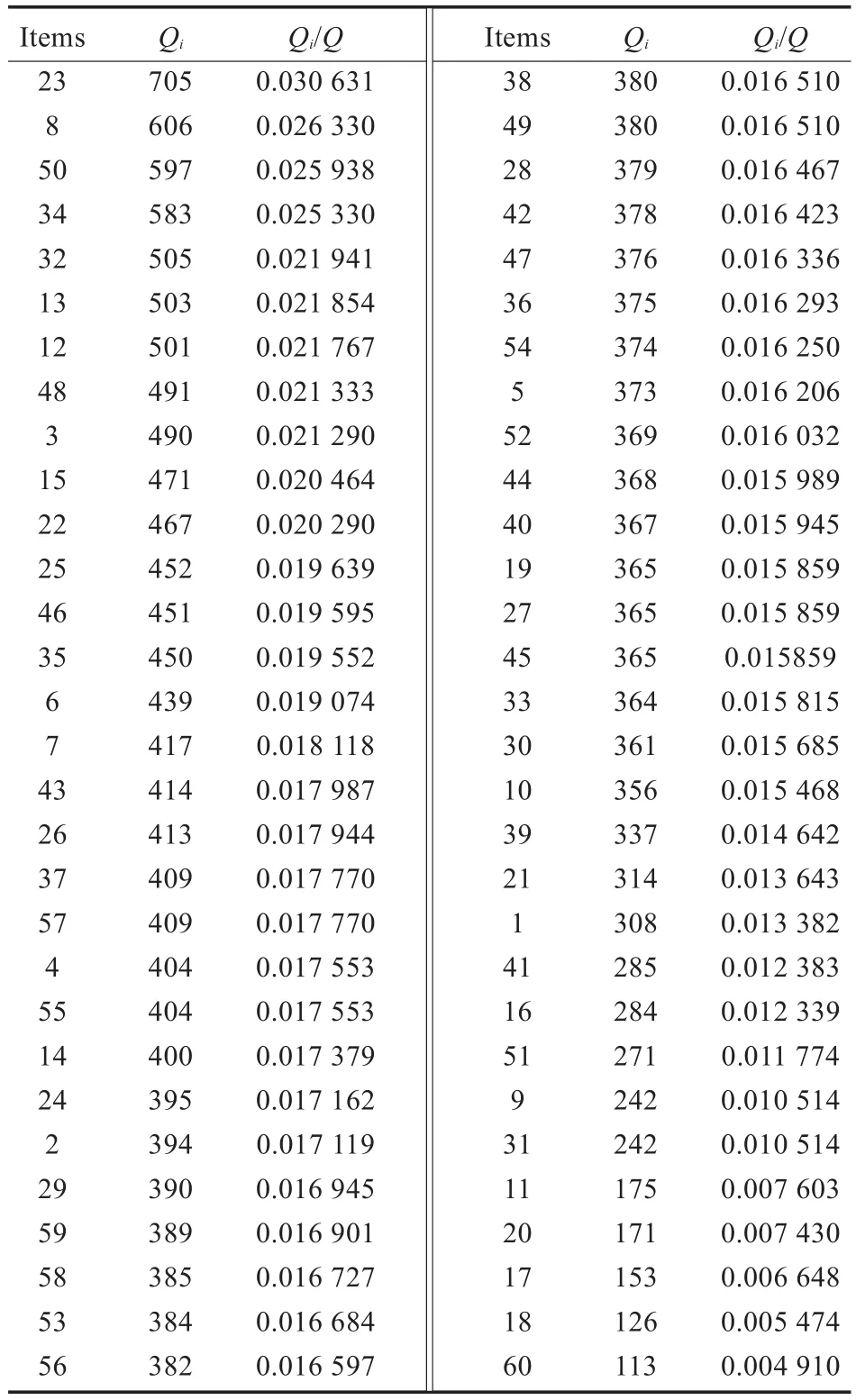
表1 品项在历史数据库中出现次数及拣选率（依次数递减统计）

图2 订单与订单品项关系图

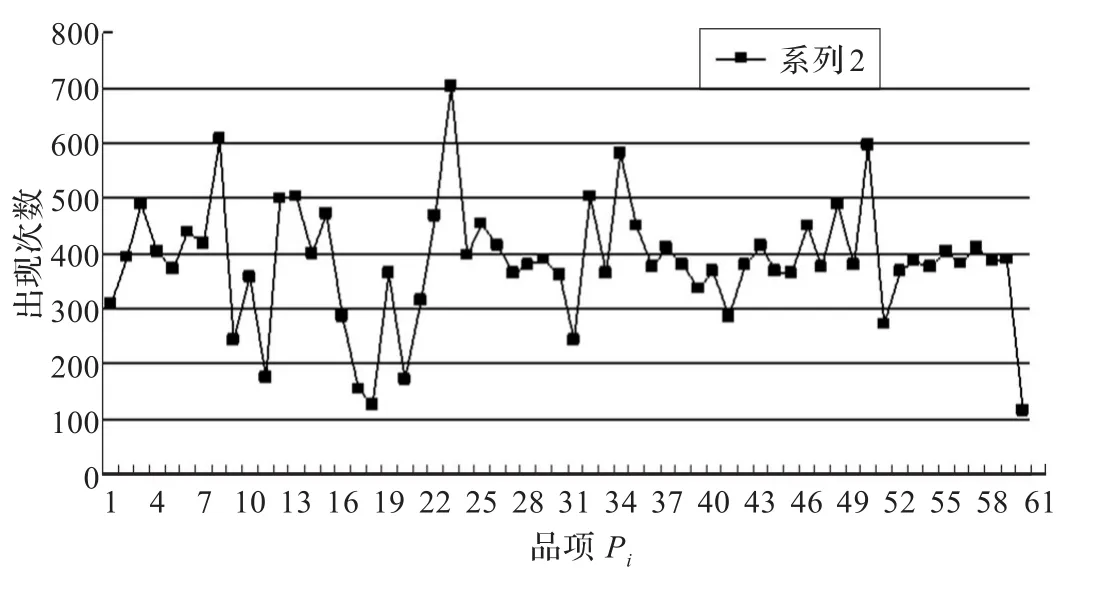
图3 订单品项出现次数统计图

由于拣货员每次拣取能力的限制，设每一品项不论其出现在一张订单还是多张订单中，其均为独立拣选。即每种品项的拣选次数等于该品项在不同订单中一共出现的次数，根据AHACAR算法对60中品项进行储位安排，其拣货效率模拟分析结果如表2所示，其中SD为订单执行率标准差。

表2 并行分区拣货系统模拟测试结果

分析表2中的数据，不论按单拣选还是批量拣选，根据AHACAR算法安排的货位，可明显改善拣货绩效，如每批次拣选5个订单，绩效改进值从平均16.72%增加到平均31.99%。此外，对于并行分区拣货系统，当结合分批策略后，即一次拣取多个订单，AHACAR算法能显著提高生产率。因为通过批量作业，可以对各分区的作业量均衡加以改善，如每批次8个订单时比每批次5个订单时，绩效提高约1.04%，这主要是由于拣货员一次处理的订单越多，可以明显减少各分区间的差异，减少等待时间使得拣货效率越高；当然，超过一定限度适得其反，这主要是订单批量的增加会导致分类时间的增加。

5 结论

本文考虑各分区拣货员拣货速度不等的情况，在分析该问题的基础上建立目标规划模型，结合品项拣选率及品项之间的关联规则，设计启发式算法，通过存储策略的改进，使拣货作业时间降低，提高了拣货效率。与传统的随机存储策略做对比，进行模拟测试，结果显示结合品项关联规则设计的AHACAR算法效果最好；研究各分区同时进行订单拣货作业的并行分区拣货系统，应用AHACAR算法进行了模拟测试，分析显示，将AHACAR算法与分批拣货策略相结合，可显著提高拣货效率。

[1]Jane C C，Laih Y W.A clustering algorithm for item assignment in a synchronized zone order picking system[J].European Journal of Operational Research，2005，166（2）：489-496.

[2]王雄志.配送中心配货作业计划方法研究[D].广州：暨南大学，2007.

[3]Rosenwein M B.An application of cluster analysis to the problem of locating items within a warehouse[J].IIE Transactions，1994，26（1）：101-103.

[4]De Koster R，Le-Duc T，Roodbergen K J.Design and control of warehouse order picking：a literature review[J].European Journal of Operational Research，2007，182（2）：481-501.

[5]Petersen C G.Considerations in order picking zone configuration[J].InternationalJournalofOperations&Production Management，2002，22（7/8）：793-805.

[6]Ho Y C，Wee H M，Chen H C.A geometric design of zonepicking in a distribution warehouse[C]//Proceedings of the International Conference on Computational Science and its Applications（ICCSA 2007），2007：625-636.

[7]Le-Duc T，De Koster R B M.Travel distance estimation and storage zone optimization in a 2-block class-based storage strategywarehouse[J].InternationalJournalofProduction Research，2005，43（17）：3561-3581.

[8]Parikh P J，Meller R D.Selecting between batch and zone order picking strategies in a distribution center[J].Transportation Research：Part E Logistics and Transportation Review，2008，44（5）：696-719.

[9]Brynzer H，Johansson M I.Design and performance of kitting and order picking systems[J].International Journal of Production Economics，1995，41（1/3）：115-125.

[10]李晓春，钟雪灵，王雄志，等.配送中心动态分区拣货系统优化设计[J].华南师范大学学报：自然科学版，2011（3）：54-60.

[11]张贻弓.基于分区拣选策略的分拣机系统综合优化研究[D].济南：山东大学，2011.

[12]王艳艳.并行自动分拣系统任务及补货缓存优化研究[D].济南：山东大学，2012.

[13]卢少平，张贻弓，吴耀华，等.自动分拣系统并行分区拣选优化策略[J].深圳大学学报：理工版，2010（1）：120-125.

[14]卢少平，张贻弓，吴耀华，等.自动拣选系统拣货区数量与品项分配综合优化[C]//Proceedings of the International Conference on Computational Intelligence and Industrial Application（PACIIA），2010：461-467.

[15]李诗珍.基于工作量均衡的分区同步拣货系统储位分配与评价[J].包装工程，2010（11）：114-118.

[16]李晓春.配送中心拣货作业设计与优化管理[D].广州：暨南大学，2009.

[17]Han Jiawei，Pei Jian，Yin Yiwen.Mining frequent patterns without candidate generation[C]//Proceedings of 2000 ACM SIGMOD International Conference Management of Data，Dallas，TX，2000：1-12.

LI Xiaochun1,ZHONG Xueling2,WANG Xiongzhi3,WANG Guoqing4

1.Department of Information Engineering and Technology,Nanhai Campus,South China Normal University,Nanhai,Guangdong 528225,China
2.Department of Computer,Guangdong University of Finance,Guangzhou 510520,China
3.College of Economics and Management,South China Agriculture University,Guangzhou 510642,China
4.Management School,Jinan University,Guangzhou 510632,China

This paper studies a synchronized zone order picking system in distribution center,considering the picker has different speed,and proposes assignment heuristic algorithm to balance the pickers’workload in different zones by the item location arrangement.Meanwhile,simulated testing is taken to validate its performance and reliability of the algorithm,which provides a reference for the application and the choice of order picking methods.

distribution center;zone order picking;assignment heuristic algorithm;data mining

主要讨论配送中心并行分区拣货系统的特性，在各分区拣货员拣货速度不同的情况下，提出储位指派算法，通过对品项在各分区间储位的安排以平衡各分区拣货员的作业量；根据拣货作业规则和优化目标，对相关模型及算法进行模拟测试以证明其有效性，为方法的选择与应用提供了依据。

配送中心；分区拣货；储位指派算法；数据挖掘

A

TP391；F276.3

10.3778/j.issn.1002-8331.1304-0069

LI Xiaochun,ZHONG Xueling,WANG Xiongzhi,et al.Storage location assignment in synchronized zone order picking systems.Computer Engineering and Applications,2013,49（19）：20-24.

教育部人文社会科学研究项目（No.09YJC630088，No.13YJC630239）；华南师范大学南海校区资助项目（No.NHZL09006）。

李晓春（1983—），女，博士，讲师，主要从事物流与供应链管理研究；钟雪灵，博士，副教授；王雄志，博士，副教授；王国庆，博士，教授。E-mail：hellolxch@139.com

2013-04-07

2013-06-01

1002-8331（2013）19-0020-05

CNKI出版日期：2013-06-18http://www.cnki.net/kcms/detail/11.2127.TP.20130618.1559.004.html