水-气二相流本构模型参数的反演识别

孙冬梅 ，冯 平，张明进，Semprich S

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 交通运输部天津水运工程科学研究所水工构造物检测、诊断与加固技术实验室，天津 300456；3. 奥地利格拉茨技术大学土力学及基础工程研究所，格拉茨 A-8010)

目前，多相流问题的研究在水文地质、石油工程及环境工程等领域迅速发展起来，多相流模型的进一步发展对地下水资源的模拟和评价、对已污染地下水土的治理与修复，以及地下水环境灾害的防治等问题具有重要意义[1-2]．在多相流数值模拟中，需要首先确定与各相流体(包括水相、气相和非水相流体（NAPL)）有关的本构关系，包括毛细压力-饱和度、相对渗透率-饱和度关系，表征这些本构关系的模型包括 Brooks-Corey(BC)模型和 Brooks-Corey-Mualem(BCM)模型、van Genuchten(VG)模型和 van Genuchten-Mualem(VGM)模型等[3-5]，这些模型中包含一组待定的与多孔介质孔隙结构特性有关的参数．在多相流情况下，同时确定水相、气相和非水相流体间的本构关系模型参数是十分困难的，基于Leverett和Lewis的定性描述，水-气二相流体的本构关系仅与各自的饱和度有关，因而目前较为有效的研究方法是首先确定水-气二相流体的本构关系模型参数，以此为基础，推求其他流体对(NAPL-气、水-NAPL)间的本构关系模型参数[6-7]，因此，确定水-气二相流体的本构关系模型参数是多相流模型研究中最基本的前提．

确定水-气二相流体的本构关系模型参数较为常用的方法是直接测量法，该方法主要通过平衡、稳态的试验来确定本构模型参数，最大的困难是进行稳态的试验通常受到初始条件和边界条件的限制，而且比较费时．近年来，随着数值计算水平及试验技术的发展，建立水-气二相流数学模型及进行有效的非稳定水-气二相流试验成为可能，采用反演识别的方法的优势越来越突显[8-10]，其主要优点是数值反演的水-气二相流试验可以是瞬态的、非稳定的流动过程，相比平衡、稳态的二相流试验要灵活、省时，而且试验的边界条件和初始条件可以自由设置，另外可以同时确定一组表征同一土样的水-气二相流体的本构关系模型参数．

采用反演识别的方法来确定水-气二相流本构模型参数的过程中，首先要进行一个非稳定水-气二相流试验来获取试验数据，试验的设计非常关键，应使得反演模型的解具有唯一性和稳定性．如 Gardner[11]所设计的单步非稳定空气出流试验就未能使得反演模型的解具有唯一性，主要原因是试验数据的信息不足；在此基础上，van Dam 等[12]进行了多步的非稳定空气出流试验，并且测量了试验过程中的累积出流量数据，从而获得了足够的试验信息使得反演模型的解具有唯一性；后来经过 Eching和 Hopmans[13]的研究表明，在非稳定水-气二相流试验中测量孔隙压力和累积出流量数据，能够使得反演模型的解具有唯一性和稳定性．因此确定水-气二相流本构模型参数的反演识别方法需要的准备工作主要包括3部分：设计合理的非稳定水-气二相流试验、能够有效模拟水-气二相流动的水-气二相流数值模拟模型以及基于最优化算法所建立的本构模型参数的反演识别模型．可见，进行水-气二相流本构模型参数的反演识别研究过程中存在许多困难，该研究是多相流数值模拟研究进一步发展的瓶颈问题．

笔者进行了多步的非稳定空气出流试验，测量了试验过程中两点的孔隙气压力、孔隙水压力、气相饱和度及累积出流量的变化过程；建立了考虑水相、气相流动及相互溶混的水-气二相流数值模拟模型，采用 Marquart-Levenberg最优化算法建立了水-气二相流本构关系模型参数反演识别模型，结合非稳定水-气二相流试验，对水-气二相流的本构关系模型(VG和VGM)参数进行反演识别．

1 非稳定水-气二相流试验

本研究所采用的试验装置如图1所示，土样放置在圆筒状树脂玻璃容器的中部，土样高度为 0.45,m，其中距离底部 1/3处和顶部 1/3处放置时间域反射计TDR(T1～T4)和压力表(P2～P3)，分别测量土柱在试验过程中的体积含水量和土柱中孔隙气压力．TDR和压力表都与数据采集器相连，试验过程数据通过计算机输出．顶部溢流出水量由电子秤测量其质量．底部与供气装置相连接，压力表 P1测量底部入流的气体压力．

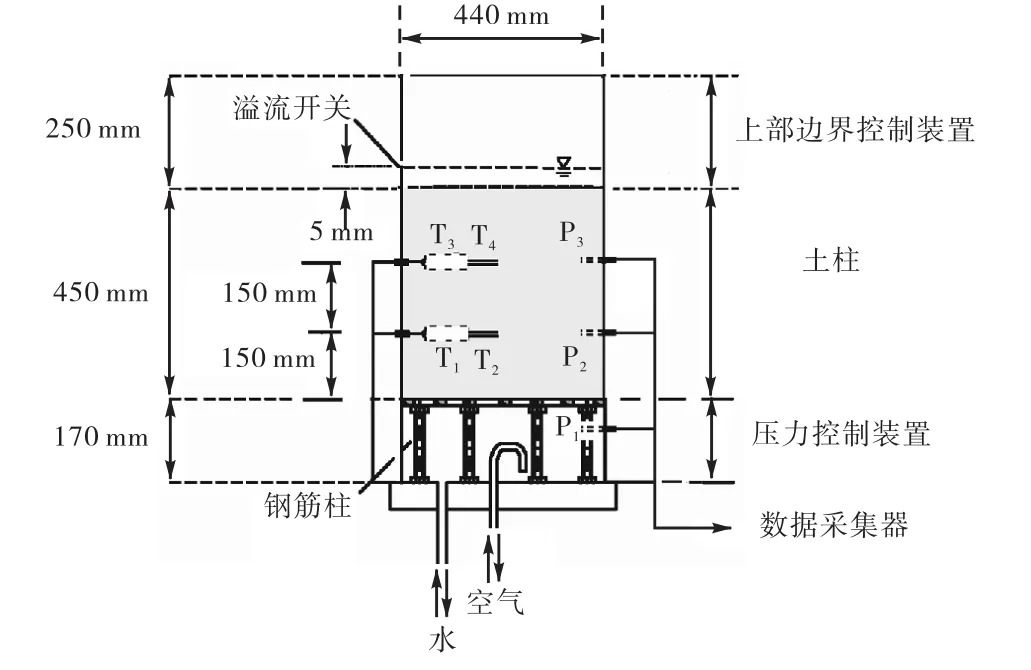
图1 非稳定水-气二相流试验装置Fig.1 Layout of unsteady water-air two-phase flow test setup

试验方法：首先将土样在搅拌机中搅拌均匀，然后将土样一层一层地放到树脂玻璃圆筒容器中，分层压实，测定此时土样的干密度和孔隙率．在分层压实的过程中，在相应的位置放置 TDR和压力表．通过对土样进行一系列常水头渗透试验，测得土样的固有渗透系数和饱和水饱和度．利用供水装置，分级增大土样顶部的水头，使土样从上而下渐进地达到饱和.最后当TDR显示的含水量达到稳定状态时即达到饱和，最后一直供水，直到土样上部的水头稳定不变，此时，土样达到稳定饱和状态，气驱替水的空气出流试验开始进行．关掉顶部的供水管，打开底部的供气管，可调节的供气装置将一定压力的气流输入到土样中，且气压力逐级增大．试验过程中，被驱赶出来的水通过溢流开关流入到量筒中，土样的体积含水量通过 TDR记录下来，压力表记录试验过程中的孔隙气压力情况．

2 水-气二相流数值模拟模型

ς为与多孔介质孔隙分布特征有关的参数；λ为与曲线形状有关的参数；pmax为最大毛细压力．

式(2)用来表征毛细压力-饱和度之间的函数对应关系．

VGM模型为

式中：krw和 krg分别为水相和气相相对渗透率；τ为迂曲度因子；参数λ和ς之间的函数关系满足λ=1−1ς．

式(3)和式(4)分别用来表征水相和气相相对渗透率-饱和度之间的函数对应关系．

通过编制计算机程序来求解上述水-气二相流模型，由于文章的篇幅有限，详细的计算程序的开发及验证工作见文献[14-15]．

3 本构关系模型参数的反演识别

2.1 基本控制方程

水-气二相流数值模拟模型的基本控制方程为水和空气这2种组分的质量守恒方程，即

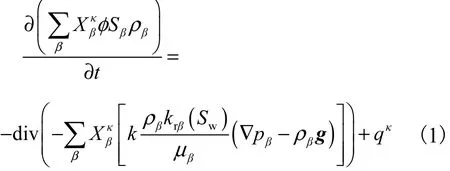
式中：κ为组分水(w)或空气(a)；β为水相(l)或气相(g)；φ为孔隙率；Sβ为β相的饱和度；ρβ为β相流体的密度；Xκβ为κ组分占β相的质量分数；q为源汇项；k为固有渗透系数；rkβ为β相的相对渗透系数；βμ为β相的黏滞性系数；pβ为β相的孔隙压力；g为重力加速度矢量．

2.2 本构关系模型

在水-气二相流系统中，VG模型和VGM模型是应用最为广泛、适用性较好的本构关系模型．VG模型为

式中：pcgw为水相和气相交界面上的毛细压力；Swe表示有效水饱和度，Swe= ( Sw− Swr) (Sws−Swr)，Sws为饱和水饱和度，Swr为剩余水饱和度；p0为进气压力；

水-气二相流本构关系模型参数的反演识别方法：首先进行非稳态的水-气二相流试验，记录试验过程中不同时刻的流场状态变量，包括累积出流量、流体饱和度和孔隙压力等，从而获取流场状态变量的瞬态测量值；利用水-气二相流数学模型对试验进行数值模拟，计算出与试验过程相应时刻的流场状态变量；采用Marquart-Levenberg最优化算法建立最小化目标函数的参数反演识别模型，以模拟值与测量值之间的误差作为目标函数，通过模拟值与测量值的比较，不断调整估计参数向量，直到满足收敛条件，从而得到最优的水-气二相流本构关系模型参数值．本研究所建立的本构关系模型参数反演识别流程见图 2．

本构关系模型参数的反演识别是一个非线性最优化问题，目标函数为实测值与模拟值之间的误差，加权最小二乘形式的目标函数为

式中：b为包含 Nc个参数的估计参数向量，通过最小化目标函数来最终确定；oq、oθ和op分别为累积出流量、体积含水量和孔隙气压力的观测值；qs、θs和ps分别为累积出流量、体积含水量和孔隙气压力的模拟值；NQ、NT和 NP分别为累积出流量、体积含水量和孔隙气压力的观测次数；wmn(m＝q，θ，p；n=i，j，k)为第n次观测时m变量的权因子．

图2 本构关系模型参数反演识别流程Fig.2 Flow chart of inverse estimation of parameters under constitutive relationship

将式(7)代入式(6)中，令目标函数 ()Ob对估计参数向量b的导数等于0，可得

在式(6)中，引入迭代指标 r，用残差向量(y−ys(b))来替代y，并且运用Marquart-Levenberg优化方法[16]，得到迭代形式的估计参数向量的增量向量 dr的表达式为

式中：mr为Marquart参数；C为对角比例变换矩阵，=(XTW X)−12；b为N×N阶的单位矩阵；ϖ为rCCr阻尼系数．

在每次迭代过程中，利用水-气二相流数学模型计算该迭代步的估计参数向量对应的与试验过程相应的模拟值向量；然后将估计参数逐个给定一个微小的增量，计算雅克比矩阵和对应的残差向量；进而运用Marquart-Levenberg优化方法，计算出估计参数向量的增量向量，从而得到下一迭代步的估计参数向量；判断是否收敛，当满足如下收敛条件之一时迭代停止，即估计参数向量中任一参数变量不大于 2%，或者目标函数的变量不大于 2%，则可得到最优的估计参数向量．

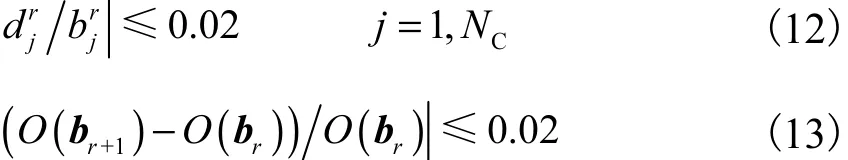
式(5)可写成统一的矩阵形式为

式中：e为残差向量；y为由 ND个观测值组成的向量；W为权矩阵；s()yb为由 ND个模拟值组成的向量，可表示为

式中X为 ND×NC阶的敏感性(雅克比)矩阵，ND为观测次数，NC为估计参数的数目．组成敏感性矩阵的元素ijX的表达式为

4 数值算例

利用水-气二相流模型对非稳定水-气二相流试验进行数值模拟，图3为模拟该试验的计算模型及网格剖分图．模型侧面的边界条件分别为：边界 1为不透水边界；上部和下部边界，即边界 2和边界 3，为Dirichlet边界条件，边界 2上的气压力为大气压力，边界 3上的气压力已知，等于压力控制室内的压力，由压力表读出．土柱处于稳定饱和状态，初始条件由试验给出．

图3 计算模型及网格剖分Fig.3 Computational model and meshes

由于试验过程中，底部气压力是逐级增加的，因此在数值模拟过程中要进行分段模拟．对于第 1阶段施加的气压力，根据初始已知的初边值条件进行模拟，得到第 1阶段末的土柱孔压、饱和度分布状态；开始第2阶段施加的气压力，将第1阶段末的渗流状态量作为初始条件进行模拟，同样得到第2阶段末的渗流状态，将其作为模拟第 3阶段渗流的初始条件，以此类推，直到模拟完最后一个阶段所施加的气压力过程，计算出与试验过程相应的模拟值向量．

VG和 VGM 本构模型中所包含的参数有：固有渗透系数 K、孔隙形状特性参数λ 和ς 、饱和水饱和度 Sws、剩余水饱和度 Swr、迂曲度因子τ、进气压力p0和最大毛细压力 pmax，其中固有渗透系数 K和饱和水饱和度 Sws通过常水头试验直接测定，K＝7.7×10-12,m2，Sws＝0.98，最大毛细压力 pmax取试验值，pmax＝1.0×107,N/m2，形状参数λ 和ς 之间存在函数关系为λ=1−1ς，因此，反演识别模型的估计参数有4个：λ、 Swr、τ和 p0．

根据文献[17]给出估计参数的初始值，利用所建立的反演模型对估计参数进行识别，经过 13次迭代达到收敛，收敛时的估计参数即为估计参数的最优值．每次迭代的目标函数值如图 4所示，估计参数的初始值和最优值如表1所示；最优估计参数间的相关性如表2所示．

表1 估计参数的初始值和最优值Tab.1 Initial value and optimal value of model estimated parameters

表2 最优估计参数间的相关矩阵Tab.2 Correlation matrix of optimal estimated parameters

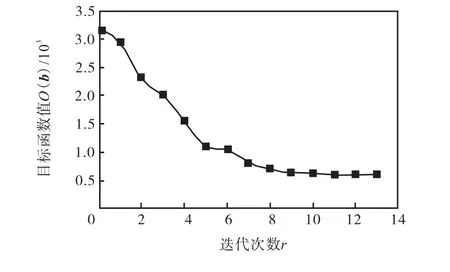
图4 每次迭代的目标函数值Fig.4 Objective function value at each iteration

估计参数最优值对应的水-气二相流模型的模拟值与试验观测值的对比曲线如图5～图7所示，其中图5为累积出流量的模拟值与实测值的对比，图6为土柱中压力表 P3位置(见图 1)的气压力模拟值和实测值对比，图 7所示的体积含水量为土样中 T2位置的模拟值和实测值．

图5 累积出流量模拟值与实测值的对比Fig.5 Comparison between simulated and calculated water outflow

图6 气压力模拟值与实测值的对比Fig.6 Comparison between simulated and calculated gas pressure

图7 体积含水量模拟值与实测值的对比Fig.7 Comparison between simulated and calculated volumetric water content

由此可见，模拟值与实测值变化趋势基本一致，考虑到试验过程中一定压力的空气入流对试验土样的扰动性及水-气二相流模型中假设土样为均匀的、各向同性的连续介质所引起的误差，所得到的拟合结果能够较好地说明估计参数最优值的准确性和参数反演模型的有效性．

将表 1所示的本构关系模型参数最优值代入到式(4)～式(6)中，即得到与试验中的土样相对应的毛细压力-饱和度、水相和气相流体的相对渗透率-饱和度关系曲线，如图8和图9所示，其中图8中pc单位为 kPa．

图8 毛细压力-饱和度关系曲线Fig.8 Relationship between capillary pressure and water saturation

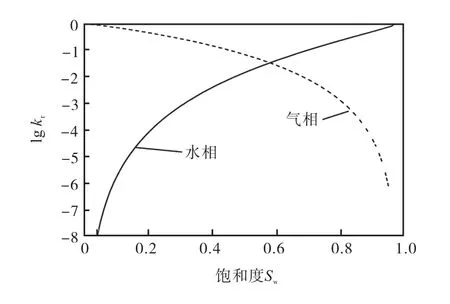
图9 水相和气相的相对渗透率-饱和度关系曲线Fig.9 Relationship between relative permeability and water saturation of water and gas phase

5 结 语

本研究进行了多步的非稳定空气出流试验，测量了试验过程中2点的孔隙压力、气相饱和度及累积出流量的变化过程；建立了考虑水相、气相流动及相互溶混的水-气二相流数值模拟模型，采用 Marquart-Levenberg最优化算法建立了水-气二相流本构关系模型参数反演识别模型，结合非稳定水-气二相流试验，对水-气二相流的本构关系模型(VG 和 VGM)参数进行反演识别．得到水-气二相流本构关系模型参数的最优估计值，分析了目标函数值在迭代过程中的变化过程，统计了最优估计参数间的相关系数矩阵，对所建立的参数反演识别模型进行了评价，将参数最优估计值对应的模拟值与试验过程的实测值进行对比分析，二者吻合较好，证明了估计参数最优值的准确性和参数反演识别模型的有效性．

在地下水多相流数值模拟研究中，确定水-气二相流体的本构关系模型参数是最基本、也是最关键的．结合非稳定水-气二相流试验，通过建立参数反演识别模型来确定水-气二相流本构关系的方法是很有优越性的，尽管该方法在具体实施过程中还可能会遇到许多困难，但是随着试验技术水平的提高及模拟试验的数学模型的进一步完善，所确定的水-气二相流模型的精度将会继续提高，因此本文的研究成果可以为确定多相流系统中与各相流体(包括水相、气相和非水相流体（NAPL)）有关的本构关系提供帮助和技术支持．

［1］ 林学钰. “地下水科学与工程”学科形成的历史沿革及其发展前景[J]. 吉林大学学报：自然科学版，2007，37(2)：209-215.Lin Xueyu. Historical change and prospect of discipline development of "Groundwater Science and Engineering"[J]. Journal of Jilin University：Earth Science Edition，2007，37(2)：209-215(in Chinese).

［2］ Helmig R. Multiphase Flow and Transport Processes in the Subsurface，a Contribution to the Modeling of Hydrosystems [M]. Berlin，Heidelberg：Springer-Verlag，1997.

［3］ Brooks R H，Corey A T. Hydraulic properties of porous medium [J]. Hydrology Paper of Colorado State University Fort Collins，1964(3)：1-27.

［4］ van Genuchten M T. A closed-form equation for predict-ing the hydraulic conductivity of unsaturated soils [J].Soil Science Society America Journal，1980，44：892-898.

［5］ Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media [J]. Water Resources Research，1976，12(3)：513-522.

［6］ Leverett M C. Capillary behavior in porous solids [J].Trans AIME，1941，142：152-169.

［7］ Parker J C，Lenhard R J，Kuppusamg T. A parametric model for constitutive properties governing multi-phase flow in porous media [J]. Water Resources Research，1987，23：618-624.

［8］ Dane J H，Oostrom M，Missildine B C. An improved method for the determination of capillary pressuresaturation curves involving TCE，water and air [J].Journal of Contaminant Hydrology，1992，11(1/2)：69-81.

［9］ Chen J，Hopmans J W，Grismer M E. Parameter estimation of two-fluid capillary pressure-saturation and permeability functions [J]. Advances in Water Resources，1999，22(5)：479-493.

［10］ 薛 强，冯夏庭，梁 冰，等. 水气两相流系统 K-SP模型参数反演的最优估计[J]. 水科学进展，2005，16(4)：488-495.Xue Qiang，Feng Xiating，Liang Bing，et al. Optimal estimation of parameters inversion for the relationship of permeability-saturation-pressure in water-air phase flow system [J]. Advances in Water Science，2005，16(4)：488-495(in Chinese).

［11］ Gardner W R. Calculation of capillary conductivity from pressure plate outflow data [J]. Soil Science Society America Journal，1956，20：317-320.

［12］ van Dam J C，Stricker J N M，Droogers P. Inverse method to determine soil hydraulic functions from multistep outflow experiments [J]. Soil Science Society America Journal，1994，58：647-652.

［13］ Eching S O，Hopmans J W. Optimization of hydraulic functions from transient outflow and soil water pressure data [J]. Soil Science Society America Journal，1993，57：1167-1175.

［14］ 孙冬梅. 水-气二相流饱和-非饱和渗流场分析及其应用研究[D]. 南京：河海大学水利水电工程学院，2007.Sun Dongmei. Study on Saturated-Unsaturated Seepage Based on Water-Air Two-Phase Flow Theory and Applications [D]. Nanjing：College of Water Conservancy and Hydropower Engineering，Hohai University，2007(in Chinese).

［15］ 孙冬梅，朱岳明，张明进. 非饱和带水-气二相流数值模拟研究[J]. 岩土工程学报，2007，29(4)：560-565.Sun Dongmei，Zhu Yueming，Zhang Mingjin. Study on numerical model for water-air two-phase flow in unsaturated soil [J]. Chinese Journal of Geotechnical Engineering，2007，29(4)：560-565(in Chinese).

［16］ Poeter E P，Hill M C. Inverse models：A necessary next step in groundwater modeling [J]. Ground Water，1997，35(2)：250-260.

［17］ Arya L M，Paris J F. A physicoempirical model to predict the soil moisture characteristic from particle-size distribution and bulk density data [J]. Soil Science Society America Journal，1981，45(6)：1023-1030.