基于单目视觉的Delta机器人零点标定方法

孙月海，王 兰，梅江平，张文昌，刘 艺

(天津大学机构理论与装备设计教育部重点实验室，天津 300072)

位置精度是抓放并联机器人的重要性能指标，运动学标定是改善其精度的有效手段之一．并联机构的运动学标定方法可大致分为两类：自标定法和外部标定法[1]．自标定法利用自身冗余传感器标定，易于实现在线标定，但无法提供机架参考系与标定测量参考系间的未知刚体位移信息，因此难以应用于实际工程．外部标定法利用外部传感器(如激光跟踪仪、经纬仪、三坐标测量仪等精密测量设备)检测末端位姿信息，构造其与模型计算值之间的残差，进而通过相应辨识模型识别几何参数．如 Zhuang等[2]利用电子经纬仪测量了Stewart平台的位姿误差全集；Maurine等[3]用激光位移传感器标定了 Delta-4型并联机器人．这些精密测量设备的共同缺点是价格昂贵、占用空间大，测量方法繁琐，数据采集时费时费力，往往需要专业技术人员精细调整，标定效率较低，难以实现快速标定，实用性差．

基于视觉的测量方法，是一种非接触式的动态测量方式，具有速度快、精度合适、灵活性高、实用性强，不影响被测目标运动和能够实现无损测量等突出优点[4]．根据摄像机成像模型，以标靶为辅助设备，通过检测标靶上特征点，即可获取摄像机坐标系在标靶坐标系中位置，进而得到检测目标在标靶坐标系中的位置信息．如 Meng等[5]和 Andreff等[6]讨论了视觉应用于机器人的标定问题．Renaud等[7]采用单目摄像机测量末端全位姿的方法对 H4机器人进行了标定实验．

在实际工程应用中，基于并联机器人生产线的现场标定要求方法简单、速度快、标定精度比较高．研究表明，对于并联机器人，零点误差是影响其精度的主要误差源，对零点进行标定可有效提高其运动精度．黄田等[8]提出一种基于末端误差最小子集检测信息的运动学标定方法．唐国宝等[9]通过仅检测末端沿z向的位置误差、以及在初始位形下的姿态误差识别出几何参数，对Delta完成了运动学标定．

在文献[8-9]基础上，以 Delta并联机器人为例，笔者提出一种基于视觉测量法的零点标定方法，并通过实验验证该方法的可行性和有效性．

1 系统分析与零点误差模型

1.1 系统分析与描述

Delta并联机器人由3个主动臂和从动臂连接静平台和动平台(如图 1所示)．主动臂经回转副和静平台连接，形如平行四边形的从动臂一端与主动臂、另一端与动平台经虎克铰球铰连接．3个主动臂在伺服电机驱动下可做高速往复摆动，从而使动平台做高速三维平动[10]．

图1 Delta机构模型Fig.1 Delta mechanism model

在加工和装配等环节通过合理的零部件加工、装配及基础精度检测工艺，可使 Delta并联机器人具备一定的基础精度：主动臂转轴轴线相对静平台基准面平行；从动臂平行四边形结构对边杆长成对保持一致；动平台加工时，其尺寸偏差和形位公差都得到严格控制，且其尺寸较小，从而在建模中可将动平台简化为一个质点O′．在保障上述基础精度前提下，根据Delta机器人的结构特点，建立 Delta机器人误差模型．

建立静平台坐标系 O -XYZ(如图 2所示)，XY平面为三转动副理想轴线所在平面，Y轴指向第2副轴线中点，原点O为XY平面与圆柱形设计空间中轴线交点．过渡系 Oi-xiyizi由系 O -XYZ绕Z轴旋转βi=− π /6 + 2 π(i − 1 )/3,(i = 1 ,2,3),βi为静平台结构角．

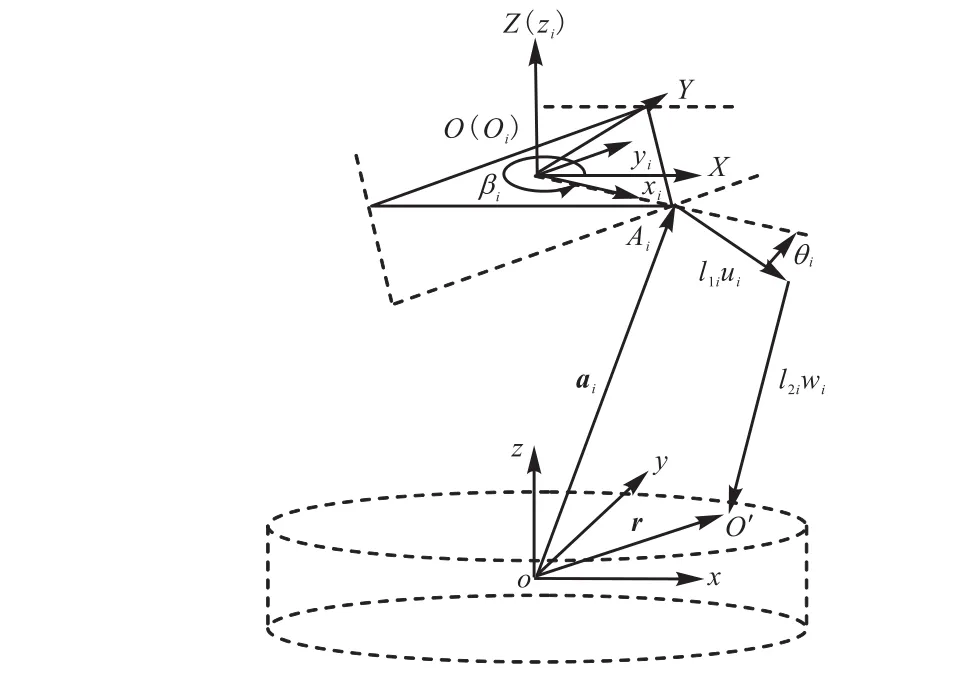
图2 Delta机器人标定坐标系Fig.2 Calibrated coordinate system of Delta robot

建立标定坐标系 -oxyz，调整Delta机器人零点位置使动平台参考点位于设计工作空间的中心，标定坐标系 -oxyz的原点o位于该中心位置，控制动平台分别沿X、Y轴运动，标定坐标系 -oxyz的x、y轴分别与其重合，z轴满足右手定则．

动平台参考点O′在标定坐标系 -oxyz中的位置矢量r可表示为

式中：ai为主动臂转动副轴线中点 Ai坐标在系 o-xyz中的位置矢量；l1i、l2i、ui、wi分别为机械手主动臂和从动臂的杆长和单位矢量；θi为主关节转角值．其中 ui可以通过坐标系变换得到：令 ui与y轴重合，然后将 ui绕Z轴转动 βi−π2，之后再绕xi轴转动−θi．上述的坐标变换可表示为

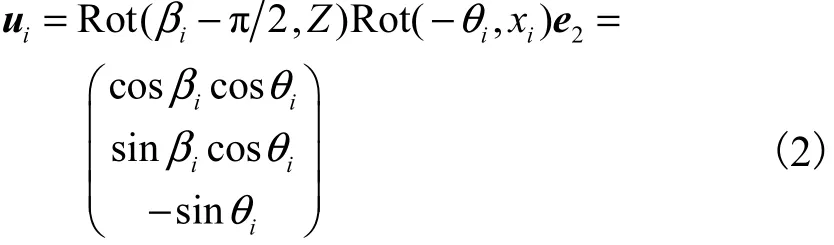
式中 e2=(0 1 0)T．

1.2 零点误差映射模型

主动臂和从动臂杆长精度易于保证，其误差可以忽略，对式(1)做一阶摄动并线性化，得

式中Δui和Δwi分别为支链i中主动臂和从动臂单位矢量的误差．式(3)两端同乘，得

式中：wi0为从动臂方向矢量名义值；且Δui=Rot(βi− π2,Z)QxRot(− θi0, xi)e2Δθi，或写成

式中0iθ为主动关节转角的理想值，其中

将式(5)代入式(4)，有

写成矩阵形式有

或

其中

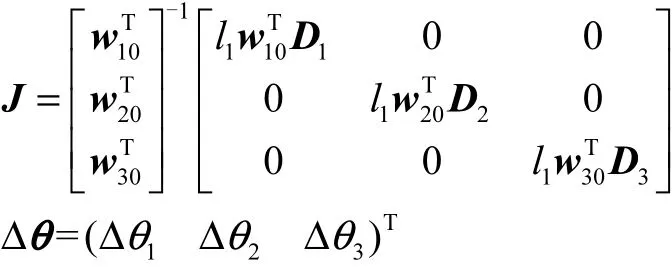
2 误差辨识模型

文献[8]从理论上证明利用并联机构操作空间非线性映射的性质，通过仅检测末端在历经所有可控自由度时沿单轴的相对位置误差及其在初始标定位形下的姿态误差即可识别出几何参数；文献[9]中以Delta机构为仿真算例，通过仅检测末端沿z向的位置误差以及在初始位形下的姿态误差便可识别出几何参数，仿真结果证明基于几何参数误差子集的精度标定可大大提高末端的位置精度．鉴于此，结合单目视觉的平面测量特点，本零点标定方法采用摄像机测量并联机器人沿标定平面运动时末端沿x、y轴向的位置误差，以辨识零点误差，误差测量原理见图3．

图3 误差测量原理Fig.3 Principle of error measurement

Delta机器人动平台末端中心点O′所在水平面为标定平面．摄像机由刚性连接板固定在动平台上，且在系统初始化调整好摄像机后，使用过程中摄像机不再调整．则摄像机⇀光心与动平台中心之间存在刚性位移(即图中)，其为常量．控制机器人动平台平移至不同位置时，则有动平台末端中心O′和摄像机光心 Oc的位移相等．因此，测得摄像机光心位置误差即等同于测得动平台中心位置误差．

机器人动平台做平移运动到某位置时，相对第 1位置在机器人标定坐标系中移动的距离 lej可表示为

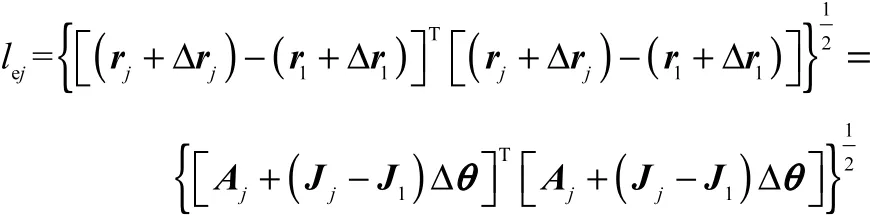
忽略高阶项，得

其中式中：m为机器人动平台平移的位置总数；jJ为系统在第j位置的误差雅克比矩阵．

测量过程中，摄像机固接在动平台末端上不做调整，则摄像机内部参数如镜头焦距、镜头畸变系数等并不改变，变化的只是摄像机外部参数．

摄像机对标定靶进行检测，根据视觉图片上特征点位置信息经摄像机标定程序可得该位置时摄像机的外部参数jR和jT，将其代入摄像机的外参模型[11]，即可求出该位置时，摄像机光心cjO(摄像机坐标系原点)在标靶坐标系中的位置，即

式中：Rj为3×3的正交变换矩阵；Tj为3×1的平移矢量矩阵．因此，机器人动平台做平移运动到某位置时，摄像机光心在标定靶坐标系移动的距离 lcj为

其中

构造任意两测点间平移距离误差函数为

写成矩阵形式有

其中

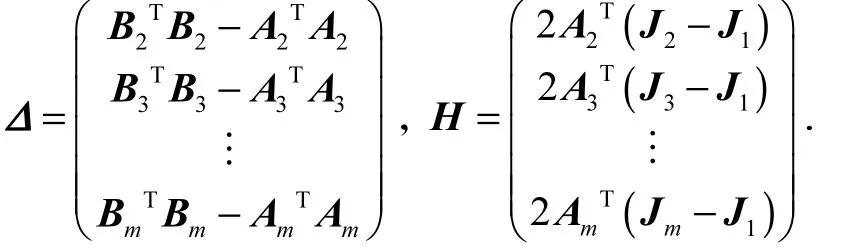
设 4m≥ ，式(14)有最小二乘解

式中 H+=(HTH )-1HT．

将辨识出的零点误差补偿到系统输入中，完成零点标定．图4给出了Delta机器人零点标定过程．

图4 Delta机器人零点标定过程Fig.4 Zero calibration process of Delta robot

3 标定实验

机器人标定实验平台如图5所示，由Delta机器人、CCD摄像头、标定靶和控制系统组成．实验采用UP680CL摄像机和 Computar M1614-MP型号镜头．摄像机由刚性连接板安装在动平台上，并设法保障摄像机成像平面和动平台平面平行．并且，摄像机经标定后，其测量精度满足机器人标定要求．图 6为实验用二维标定靶，包括4055×个直径为5,mm的圆形靶点，各靶点之间间距为 10,mm．二维标靶放置在生产线上，并保证标靶平面与摄像机成像平面平行．在实验过程中，标靶不再改变位置．选择标靶坐标系作为世界坐标系，标靶系原点在标靶左下角．

图5 零点标定实验平台Fig.5 Experimental platform of zero calibration

图6 标定靶Fig.6 Calibration target

零点标定之前，对 Delta机器人进行初调，采用目视法使主动臂处于大致水平位置．控制动平台在z= 0 高度平面内运动至若干位置，采用 Leica-AT901-LR型激光跟踪仪检测标定前机器人末端的位置误差为，结果如图7所示．标定前位置误差最大值为1.442,mm，平均值为0.932,mm．

图7 标定前末端位置误差Fig.7 Position error of end-effector before calibration

标定实验包括数据采集和参数标定 2部分．数据采集时，在保证标靶在摄像机视觉范围的情况下，控制动平台在某一高度(本实验为100,mm)平面内平移至 20个位置，记录该位置处主动关节传感器读值θij( i = 1 ,2,3, j = 1 ,2,… ,2 0)和控制器显示的位置坐标rj(j=1,2,… ,2 0)，同时拍摄视觉图片．其中，选择的动平台测点位置在机器人工作区域内呈均匀分布．

参数标定则是将采集的实验数据作为输入，代入到前面建立的误差映射模型和辨识模型进行计算．具体如下．首先，视觉图像经图像处理分析、摄像机标定可得摄像机外部参数 Rj和 Tj( j =1,2,… ,20)，代入式(12)可得 Bj．其次，将 rj代入理论逆解模型得出相关数据，并代入误差映射模型得 Jj．另外将 rj代入式(9)可得 Aj．将 Aj、Bj、Jj代入距离误差函数(即式(14))，可求得并联机器人零点误差Δθ，数值如表 1所示；并用解得的零点误差修改零点位置，完成零点标定．

表1 零点误差Tab.1 Zero error rad

标定后机器人在 z＝0高度平面内末端的位置误差分布如图 8所示．标定后位置误差最大值为0.374,mm，平均值为0.211,mm．

图8 标定后末端位置误差Fig.8 Position error of end-effector after calibration

综上检测结果，零点标定使机器人末端位置精度从 0.9,mm左右提高到 0.2,mm左右，机器人的定位精度得到有效提高，证明零点标定方法是有效的．以文献[10]中基于激光跟踪仪的 Delta机器人的运动学标定方法为例做比较，零点标定方法标定结果较前者精度稍低，但零点标定方法较其具有误差模型简单、测量数据简便、快速、易操作等优点．综合考虑，零点标定方法更适合于工程应用中的现场标定．

4 结 论

(1) 运用空间矢量法，合理设定标定坐标系，构建零点误差模型，并建立基于视觉测量法的包含零点误差的参数辨识模型；依据该模型仅检测动平台沿水平面运动时末端x、y向的位置误差，便可将零点误差辨识出来．

(2) 利用激光跟踪仪对 Delta机器人零点标定前后的位置精度进行测量，标定后的动平台位置精度从 0.9,mm左右提高到 0.2,mm左右，验证了该方法的可行性和有效性．

(3) 基于视觉测量的零点标定方法，测量设备普遍、易携带，测量方法简单、快速、现场实施性强，标定精度满足一般工程需求，便于在工程中实施．

［1］ 丛 爽，尚伟伟. 并联机器人——建模、控制优化与应用[M]. 北京：电子工业出版社，2010.Cong Shuang，Shang Weiwei. Parallel Robots—Modeling，Control Optimization and Applications[M].Beijing：Publishing House of Electronics Industry，2010(in Chinese).

［2］ Zhuang Hanqi，Masory O，Yan Jiahua. Kinematic calibration of a Stewart platform using pose measurements obtained by a single theodolite[C] // Proceedings of IEEE International Conference on Intelligent Robots and Systems. Pittsburgh，USA，1995：329-334.

［3］ Maurine P，Dombre E. A calibration procedure for the parallel robot Delta 4[C] // Proceedings of IEEE International Conference on Robotics and Automation. Minneapolis，USA，1996：975-980.

［4］ 张淑平. 基于视觉的并联机器人位姿检测方法研究[D]. 上海：东华大学信息科学与技术学院，2010.Zhang Shuping. Stereo Vision Based Position and Posture Estimation of Parallel Manipulator[D]. Shanghai：College of Information Science and Technology，Donghua University，2010(in Chinese).

［5］ Meng Y，Zhuang Hanqi．Autonomous robot calibration using vision technology[J]. Robotics and Computer-Integrated Manufacturing，2007，23(4)：436-446.

［6］ Andreff N，Martinet P. Vision-based self-calibration and control of parallel kinematic mechanisms without proprioceptive sensing[J]. Intelligent Service Robotics，2009，2(2)：71-80.

［7］ Renaud P，Andreff N，Lavest J-M，et al. Simplifying the kinematic calibration of parallel mechanisms using vision-based metrology[J]. IEEE Transactions on Robotics，2006，22(1)：12-22.

［8］ Huang Tian，Wang Jinsong，Chetwynd G D，et al.Identifiability of geometric parameters of 6-DOF PKM systems using a minimum set of pose error data[C] //Proceedings of ICRA. Taipei，China，2003：1863-1868.

［9］ 唐国宝，黄 田. Delta 并联机构精度标定方法研究[J]. 机械工程学报，2003，39(8)：55-60.Tang Guobao，Huang Tian. Kinematic calibration of Delta robot[J]. Chinese Journal of Mechanical Engineering，2003，39(8)：55-60(in Chinese).

［10］ 李 毅. 高速并联机械手运动学标定方法研究[D]. 天津：天津大学机械工程学院，2009.Li Yi. Kinematic Calibration Method for High-Speed Parallel Robot[D]. Tianjin：School of Mechanical Engineering，Tianjin University，2009(in Chinese).