船坞虹吸灌水廊道驼峰压强计算及最优半径的确定
2013-07-19白玉川马金辉戚晓明
白玉川,赵 鹏,马金辉,戚晓明
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 海洋石油工程股份有限公司,天津 300451)
建造大型干船坞,灌水方式的选择是工程中较为关心的问题,所使用的灌水方式应简单高效,且易于维护管理.国内大型船坞的灌水方式主要有坞门灌水、短廊道灌水和虹吸廊道灌水 3种形式.前两者均需使用大型阀门,由于长期受到海水腐蚀,易引起阀门关闭不严导致干船坞漏水的问题.相比较,虹吸廊道不设阀门,结构简单、运行方便且断流迅速,近年来在新建修造船坞得到了广泛使用[1].
大型干船坞对灌水时间有严格的控制,特别是修船坞,由于船舶进出坞频繁,为提高工作效率,船坞灌水时间一般控制在 1.0~2.5,h,这就要求虹吸廊道能够提供足够大的灌水流量.由于廊道驼峰底高于海面,且水流受沿径向向外的离心力作用,过高的流速使得驼峰底部压强降低,有可能会对廊道壁面产生空蚀破坏,影响廊道使用寿命.因此在使用虹吸灌水廊道时,虹吸段的设计特别是虹吸半径的选择显得尤为重要.目前已有研究主要集中在驼峰负压符合规范要求的前提下,如何使廊道过流能力达到最大,保证船坞运行效率.笔者主要对虹吸段的水力特性进行了理论分析,并在此基础上建立了虹吸段最优半径的计算方法[2-4].
1 虹吸段水力特性的计算
1.1 柱坐标系控制方程
在图 1所示的柱坐标系下建立不可压流体运动控制方程如下.
(1) 连续方程为
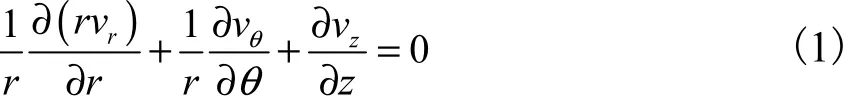
(2) N-S方程有3个分量,分别如下.
r分量:

θ分量:

z分量:
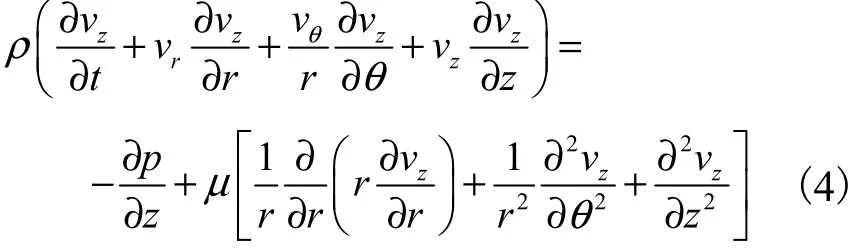
式中:vr、vθ和 vz分别为水流径向、切向和轴向速度;ρ为水的密度;μ为动力黏度;gr和 gθ分别为单位重力的径向和切向分量.
控制方程的边界条件为:r=R1,vθ=0,r=R2,vθ=0;R1、R2分别为外壁、内壁半径.

图1 虹吸廊道示意Fig.1 Sketch of siphon tunnel
1.2 虹吸段流速分布推导
通过观察模型试验中廊道掺气形成的气泡可发现,水流在虹吸段无剧烈掺混,基本做圆周运动,轴向和径向的流速较小,可假设 vz=0,vr=0,将此条件代入控制方程组可得

由式(8)可知:p 为(r,θ)的函数,即 p=p(r,θ).式(6)对r求积分,可得驼峰压力分布p的表达式为
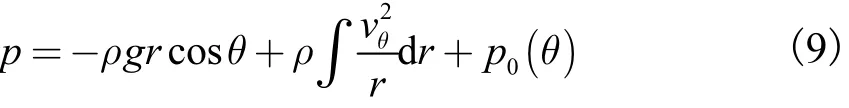
式(9)对θ求导得

将式(10)代入式(7),化简得
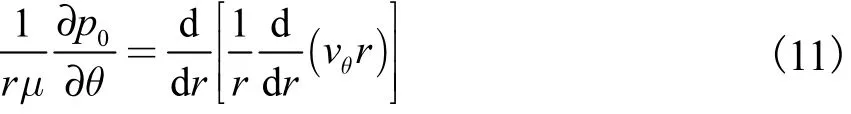
对r进行2次积分并引入积分常数c1、c2,可得

将边界条件 r=R1,vθ=0 和 r=R2,vθ=0 代入式(12)中可解出积分常数c1和c2分别为

将 c1和 c2代入式(12),可求得驼峰断面流速分布为

式(12)对r求积分可得出驼峰段的平均流速为
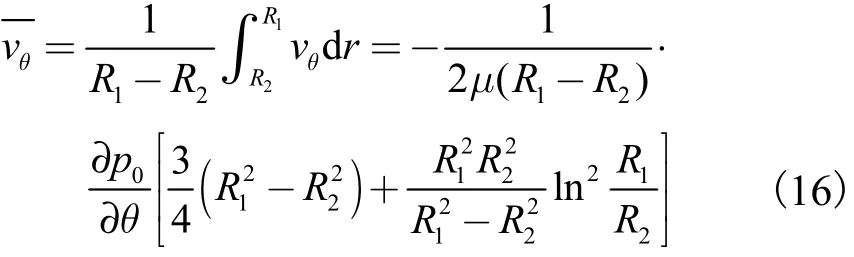
记灌水流量为 Q,驼峰宽度为 W,驼峰断面高度为H,则存在关系

将式(17)代入式(16),并有 H=R1-R2,可得∂ p0∂θ 的计算式为

再将式(18)代入式(15)即可求得vθ的表达式为

式(19)即为驼峰流速 vθ的表达式,在廊道体型参数和灌水流量确定后,可通过此式求出驼峰的流速分布,但工程中相较驼峰断面的压强分布,一般并不关注流速的绝对值.
1.3 驼峰断面压强分布推导
vθ的表达式求出后,即可求出虹吸段的压强分布.为便于推导,对式(18)、式(19)中的参数简化为

则式(19)可简化为
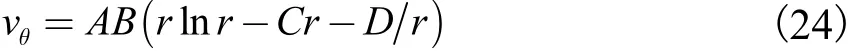
将式(24)代入式(9)进行积分运算,可得到虹吸段压强分布的计算式为
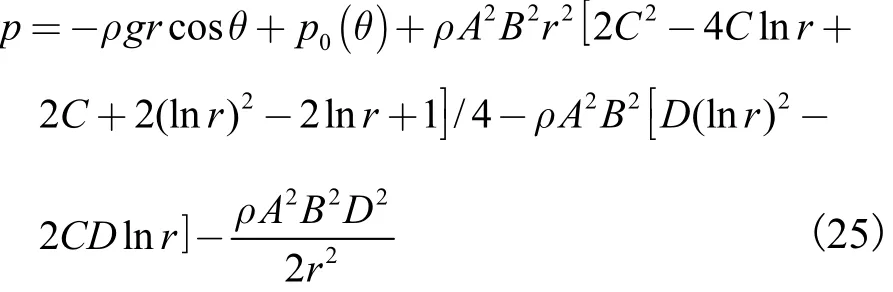
当 θ=0时,即为驼峰断面的压强分布计算式.式中积分常数 p0(θ)可使用文献[5]中的方法确定.即设驼峰断面中心处的压强为pc,代入式(25)可得

式中R为虹吸段中心线半径,所以有

将积分常数p0(θ)代回式(25)并简化得

式中 pc可不考虑驼峰的局部阻力,在海水面和驼峰中心处列伯努利方程计算.
2 虹吸段最优半径的确定
合理地选择虹吸段半径以避免驼峰底产生较高的负压,可提高驼峰的高程,或高程不变,增大灌水流量,这对灌水系统的高效运行是有利的.一般将使驼峰断面上压强分布均匀的虹吸段中心线半径称为最优半径.
现考虑一种理想状态即驼峰断面压强沿径向相等.即当θ=0,可导出关系式

将式(29)代入式(6)得

即廊道虹吸段具有最优半径后,在驼峰断面水流流速vθ应与半径r满足式(30).
在驼峰断面的顶部,半径r=R1,式(30)可写为

在上面已经求出vθ的表达式,将式(31)展开为
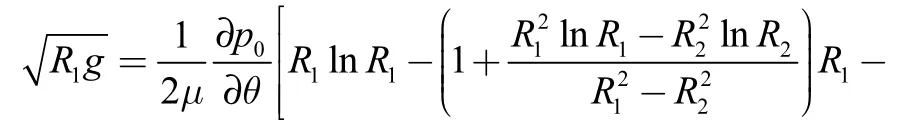

式(30)中含有∂p0∂θ、R1、R23个未知量,代入∂p0∂θ表达式,并考虑H=R1-R2,式(32)可写为

现在考虑另外一种情况,在驼峰断面的底部,半径 r=R2,式(30)可写为

同样代入0p∂∂θ的表达式,并考虑H=R1-R2,则有

式(33)和式(35)为驼峰断面压强分布均匀,即虹吸段半径为最优半径时,虹吸段外径、灌水流量和驼峰断面高度应满足的关系.可以看出,由式(33)和式(35)求出的 R1是不相等的,说明驼峰顶部和底部要求的最优半径是不相同的.但是工程上驼峰断面压强绝对均匀是不可能的,只要近似均匀即可.为此虹吸段的外径取二者的平均值,将使用驼峰断面顶部求出的虹吸段外径记为 R1′,使用驼峰断面底部求出的虹吸段外径记为 R1′,虹吸段外径 R1= ( R1′ + R1′′)/2,则最优半径 R = R1− H 2.
以设计灌水流量为 Q=40,m3/s,驼峰宽度 W=4,m,驼峰断面高度 H=1.5,m的虹吸灌水廊道为例,将式(33)和式(35)移项后记做f(R1)=0,并使用图解法求解,如图 2和图 3所示,得出 R1′= 4 .55m,R1′= 6 .02m,则虹吸段外径 R1= 5 .29m,相应的最优半径为4.54,m.
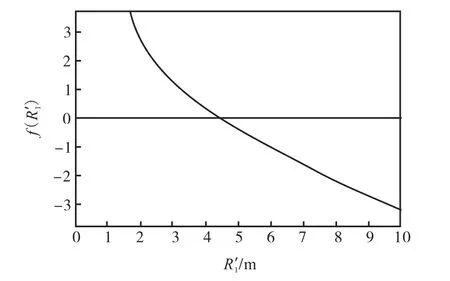
图2 图解法求解 R 1′示意Fig.2 Sketch of solving by graphical solution

图3 图解法求解 R 1′′ 示意Fig.3 Sketch of solving R1′′ by graphical solution
3 压强分布公式的模型试验验证
对于驼峰断面压强计算式(28),本文使用中船龙穴 1号修船坞虹吸灌水廊道的水力模型试验数据对其进行了验证,廊道相关参数如下:驼峰宽度W′=4.20,m,外径R1=5.67,m,内径R2=4.33,m,驼峰底高程 5.20,m,设计进出坞水位 2.20,m.模型试验实测廊道进口至驼峰的局部阻力系数ξ=0.367.则不同水位下灌水流量和用伯努利方程计算出的pc见表1.

表1 不同水位下的Q和pc值Tab.1 Q and pc on different water levels
图4为各水位下,压强计算值与模型试验值的对比,其中h为测点高程.可以看出,计算值与试验值符合较为理想,式(28)总体上能反映不同水位下断面压强的变化趋势.虽部分测点偏差较大,但对于较为关注的驼峰底压强,计算值与试验值相差小于 2.00×103,Pa.相比较文献[4]要求驼峰的最小压强为 2.29×104~3.27×104,Pa,式(28)可满足工程预测需要.

图4 不同水位下压强计算值与模型试验值对比Fig.4 Comparison of calculated and model testing pressures on different water levels
4 最优半径计算公式的分析与验证
4.1 与文献[5]公式的对比分析
文献[5]假定虹吸段流动为势流,导出驼峰断面上压强分布的理论计算公式.并使峰顶压强等于峰底压强,给出了虹吸段中心线的曲率半径 R的计算公式.
图 5为不同灌水流量,驼峰高度 H为 1.0,m、1.5,m、2.0,m 和 2.5,m 时,文献[5]与本文虹吸段最优R的对比.当 H=1.0,m 时,文献[5]与本文得出的R值相近,差值小于2,cm.H=1.5,m时,在灌水流量较小时,本文计算出的 R值较大,随着灌水流量的增大,2种方法得出的 R值趋于一致.在 H=2.0,m和2.5,m 时,由于文献[5]中的计算方法要求(H /2)/(v2/2g)< 1 ,所以在低灌水流量时无解;相比文献[5],在不同灌水流量下,本文得出的 R值偏大约 4~20,cm.
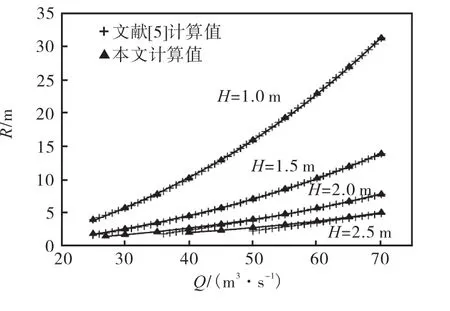
图5 虹吸段中心线半径R对比Fig.5 Comparison of siphon radius R
为比较2种方法得出的虹吸段最优半径,建立了2组典型工况下具有不同半径的虹吸段数值模型,分别计算了它们的驼峰断面压强分布.由于数值模型相对简单,且篇幅有限,在此不再赘述.
图6和图7分别为驼峰断面高度H为2.0,m和2.5,m时的驼峰断面压强分布对比,灌水流量Q取值为 55,m3/s和 70,m3/s,为方便对比,已将峰底压强统一.2种方法得出的最优半径相差约0.1,m,相比较本文半径下的断面压强分布更为均匀,峰顶和峰底压强也较为接近.从图 7中可看出,H=2.5,m 时峰顶峰底压强差较大,说明离心力没有得到合理利用,对于这种驼峰断面高度较大的工况,可考虑再引入断面中心点vθr=R=,取 3点平均以对最优半径进行校正.

图6 压强分布对比(Q=55,m3/s)Fig.6 Comparison of pressure distribution(Q=55,m3/s)
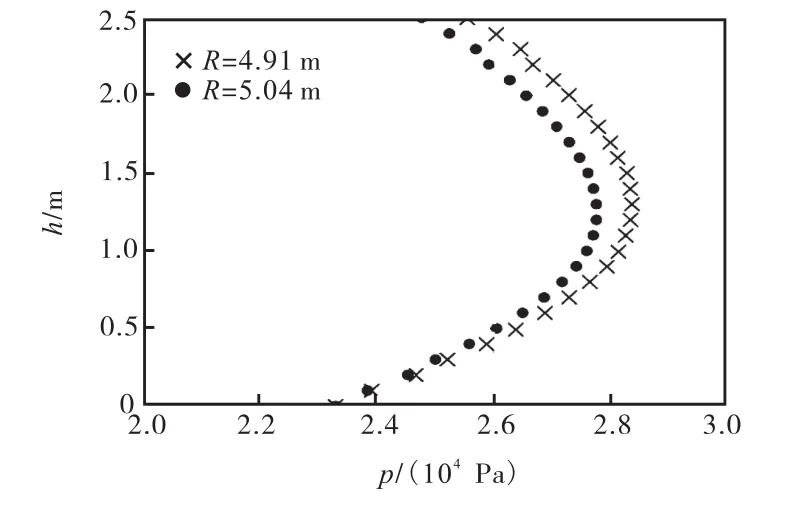
图7 压强分布对比(Q=70,m3/s)Fig.7 Comparison of pressure distribution(Q=70,m3/s)
4.2 公式的应用验证
为进一步验证本文方法的有效性,对大连船舶重工修船 1号修船坞灌水廊道的虹吸段半径进行了优化.其设计体型参数基本与中船龙穴 1号修船坞相同,驼峰底高程 3.70,m,设计进出坞水位 1.31,m.设计水位下模型试验实测灌水流量 42.09,m3/s,驼峰断面上压强分布试验值见图 8,其中 R=5.00,m为虹吸段中心线半径设计值,R=5.77,m 为使用本文最优半径计算方法得出的中心线半径.同时使用数值计算的方法给出了 2个中心线半径下的驼峰断面压强分布,且R=5.00,m的计算值与模型试验值对比表明计算结果是可信的[6].
从图8中可以看出,在R=5.00,m下,断面最小压强在驼峰底,为 3.59×104,Pa,最大压强在驼峰顶,为 3.83×104,Pa,这说明虹吸段半径值偏小造成离心力过大.当 R=5.77,m 时,断面压强分布较前者均匀,驼峰底和驼峰顶压强差值小于 347,Pa,且峰底压强升高了0.17×104,Pa,这对防止空化是有利的.
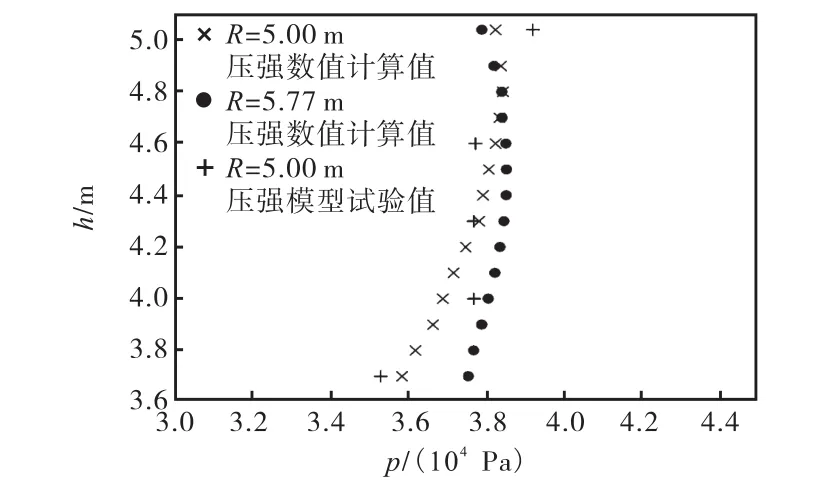
图8 驼峰断面压强对比Fig.8 Comparison of pressure distribution on hump
5 结 语
本文针对虹吸灌水廊道工程中关心的驼峰负压和虹吸段最优半径问题,在柱坐标系下建立虹吸段水流运动方程并适当简化,推导出了驼峰断面的流速和压强解析表达式.使用压强表达式计算得出的某廊道驼峰断面压强分布与水力模型试验值吻合较好,表明其可用于初步设计后驼峰压强的估算,以防止工程运行中廊道壁面的空蚀破坏.在压强表达式的基础上提出了虹吸段最优半径的确定方法,与已有方法得出的最优半径下的断面压强分布相比,本文方法的峰顶峰底压强更为接近,说明离心力得到了合理利用,有利于防止空化的发生.最后本文对一廊道的虹吸段半径进行数值优化试验,进一步验证了虹吸段最优半径确定方法的有效性.
[1] 杨浩俊,陈立新. 船坞灌水技术[J]. 水运工程,2009(8):108-114.Yang Haojun,Chen Lixin. Dock's filling technology[J]. Port and Waterway Engineering,2009(8):108-114 (in Chinese).
[2] 白玉川,张效先. 山海关船厂 15万吨级修船坞虹吸灌水水力模型试验研究[J]. 船舶力学,2003,7(4):36-49.Bai Yuchuan,Zhang Xiaoxian. Hydraulic modeling studies for filling water by a new type of siphon passage in the 15 ten-thousand-ton class lay-up dock of Shanhaiguan dockyard [J]. Journal of Ship Mechanics,2003,7(4):36-49(in Chinese).
[3] 张效先,杨建华,白玉川. 修、造船坞虹吸灌水流道的设计方法[J]. 天津大学学报,2006,39(2):204-208.Zhang Xiaoxian,Yang Jianhua,Bai Yuchuan. Design of the siphon piping of the ship repairing-building dock[J]. Journal of Tianjin University,2006,39(2):204-208(in Chinese).
[4] 中华人民共和国交通部. JTJ 253—87 干船坞坞门及灌水排水系统设计规范[S]. 北京:人民交通出版社,1987.Ministry of Transport of the People's Republic of China.JTJ 253—87 Standard for Design of Dock Gates and Filling and Emptying Systems of Dry Docks[S].Beijing:China Communications Press,1987(in Chinese).
[5] 习和忠,王常生,陈秀玉. 虹吸式输水管道驼峰断面上压强分布的计算[J]. 水运工程,1987(7):8-12.Xi Hezhong,Wang Changsheng,Chen Xiuyu. Pressure calculation of hump section in siphon passage [J]. Port and Waterway Engineering,1987(7):8-12(in Chinese).
[6] 赵 鹏,白玉川. 船坞虹吸灌水廊道水力特性的数值模拟[J]. 天津大学学报,2011,44(10):920-924.Zhao Peng,Bai Yuchuan. Numerical simulation of hydraulic characteristics in siphon passage of dockyard [J].Journal of Tianjin University,2011,44(10):920-924(in Chinese).
