复杂层状岩基上重力坝极限抗震能力评估方法初探
2013-07-19张社荣王高辉
张社荣,王 超,孙 博,王高辉
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
在重力坝全生命周期的运行中,大坝性能可能受到诸如超标洪水、地质条件恶化、建筑材料老化乃至远远超过设计地震动水平的极端地震荷载的威胁.特别是5.12汶川地震以来,重力坝极限抗震能力受到极大关注,逐渐成为抗震安全性评价中的热点问题.然而,由于世界上重力坝震害典型实例较少[1-2],人们对极端地震作用下重力坝的破坏机理和失效模式的认识并不充分.
研究混凝土重力坝极限抗震能力及其在地震过程中的破坏模式主要有室内模型试验、数值试验及理论分析等方法.范书立等[3]采用仿真混凝土材料制作龙开口水电站溢流坝段的模型,考虑坝体-库水的动力相互作用,研究了溢流坝段的坝体开裂形式和抗震能力.但是,由于影响混凝土重力坝动力响应和破坏形态的因素很多,诸如地基和混凝土的各向异性、不确定性等,模型试验无法全部考虑,因此还需结合数值计算结果才能做出全面的评价.此方面,李 昇 等[4]采用超地震荷载法研究强震作用下重力坝的破坏模式;周伟等[5]利用三维非线性有限元法,研究了坝基的渐进破坏模式和坝体坝基系统的极限承载能力;Ghanaat[6]根据线弹性时程分析得到的应力需求能力比、超应力累积持时及超应力分布范围等抗震性能参数,提出了混凝土坝抗震损伤程度的定量分析方法和评价标准;沈怀至等[7]提出了基于功能的混凝土重力坝地震破坏定量评价模型;Pekau等[8]使用离散单元法(discrete element method,DEM)研究混凝土重力坝脱离体的极限抗震能力.但是,对于重大工程典型实例,基于数值试验的极限抗震能力的分析评价方法及其适用性还有待深入探讨.
阿海水电站工程区地震地质背景复杂,坝址区设计烈度接近Ⅸ度,其 100,a超越概率 2%的基岩水平地震动峰值加速度(peak ground acceleration,PGA)达0.344,g.大坝建基岩体主要为板岩砂岩互层结构,复杂层状岩体地基上的大坝极限抗震能力是本工程的关键技术问题.
笔者以阿海水电站工程作为分析实例,结合基于功能的地震破坏等级评价模型、基于断裂力学的坝体非线性行为分析模型和基于收敛性判据的系统极限抗震稳定性分析评价模型,采用地震动超载时域分析方法,建议从坝体混凝土损伤破坏等级、开裂破坏模式、坝基岩体塑性区破坏扩展规律、坝体坝基系统稳定性突变等方面综合评价其极限抗震能力.
1 评价模型及研究方法
采用数值方法分析重力坝的极限抗震能力,目前还没有统一的评价标准可以参照,通常采用非线性计算收敛性准则.但是,所采用的数学模型、破坏准则、单元类型、边界条件等因素均可能对数值计算结果及其收敛性产生不同程度的影响,且目前缺乏有效的方法来消除这些因素的影响;且从基于性能的抗震设防标准及理论出发,往往是坝体某个关键性能(如大坝蓄水功能)破坏便会影响到坝体正常运行.因此,单一的评价准则已经不能满足大坝极限抗震能力评估的要求.
极限地震荷载下的系统功能失效是重力坝达到极限抗震能力的重要表征.高混凝土坝破坏机理关键[9]在于2个方面,一是非连续(节理、断层、软岩)坝基岩体在蓄水或强地震下发生变形、滑动;二是大坝混凝土在蓄水与强地震作用下发生强度断裂.极端荷载条件下,其潜在失效模式主要体现在以下3个方面[5]:超拉应力开裂;倾倒突变失稳破坏;沿坝体坝基薄弱层面滑动.它们是评判大坝是否达到极限抗震能力的关键因素.采用数值分析方法时,就需要将结构系统的屈服破坏准则、塑性区贯通、系统状态突变等判据综合考虑.
1.1 基于性能的地震破坏评价模型
基于坝体安全评价理念和弹塑性损伤理论[7],首先采用线弹性分析方法,结合 Ghanaat[6]提出的破坏等级划分标准,初步定量评估大坝的损伤破坏程度.坝体线弹性分析中的需求能力比(demand to capacity ratio,DCR)最大允许值以地震荷载下名义抗拉强度即 DCR=2为分界点,结合超应力累积持时,将地震荷载下坝体破坏程度分为低-中等与严重损伤2个区域.
然后,采用能够模拟混凝土非弹性现象且能够严格定义破坏面演化准则的连续式塑性损伤力学模型,进行坝体坝基系统的非线性分析,研究其塑性损伤行为规律.其损伤本构方程为

式中:ijσ为有效应力;,klijD为损伤刚度矩阵;d为损伤张量,其中包含拉压损伤因子;el,,klijD 为初始未损伤的弹性刚度矩阵;klε为总应变;pl,klε为塑性应变[10].
1.2 基于断裂力学的坝体开裂破坏模型
采用William-Warnke 五参数准则[11]判断混凝土的屈服和破坏.在屈服以前,采用等效单轴模型模拟混凝土的本构关系,在混凝土开裂后,采用无网格方法的弥散裂缝模型[12]模拟其开裂行为.弥散裂缝模型通过非弹性开裂应变等效模拟裂缝,通过调整材料软化本构关系,无需改变单元形式或重新划分单元网格;引入垂直于裂缝表面方向上的一个缺陷平面来表示在某个积分点上出现开裂.
利用 William-Warnke 五参数屈服准则可以确定混凝土的最终强度曲面,保证了破坏面的连续性.William-Warnke五参数(即单轴抗拉强度tf、单轴抗压强度cf、二轴等压强度cbf、拉子午线上的三轴强度1f以及压力子午线上的三轴强度2f)准则,2个子午面之间的椭圆极坐标关系为


式中1r和2r分别为受拉子午面和受压子午面上的极坐标值,且有

当单元达到开裂状态时,单元在最大主应力垂直的方向形成无数平行的微裂纹,单元发生损伤,即对单元的本构关系进行修正,并在本构模型中引进剪力因子考虑开裂的软化特性.能自动确定裂缝起裂、扩展的完整信息,具有较高的计算效率.基于此,在动力计算中,不必随着裂缝出现和发展而改变有限元网格划分,可以有效表达动力工况下混凝土开裂行为.
混凝土拉裂后破坏面的法向刚度和剪切刚度降低,如果裂缝重新闭合,又可重新传递压应力,残留抗剪系数增大.混凝土压碎后,单元刚度变得很小,对总体刚度的贡献可以忽略.
沿裂缝面建立正交坐标系,以应力应变全量的形式描述材料开裂后的力学行为(平面应力问题),经过改进[13],混凝土材料发生开裂后应力应变关系[14]为

式中:E为弹性模量;ν为泊松比;σ和τ分别为正应力和剪应力;εγ和分别为正应变和剪应变;下标ns和分别表示垂直和平行裂缝的方向;G为剪切模量;β为剪切抗力系数,01β≤≤;μ为随开裂应变变化的法向弹模折减系数.在有限元程序实现过程中,裂缝张开剪力传递系数取为 0.5,裂缝闭合剪力传递系数取为0.9.
1.3 坝基动力极限承载能力评价模型
1.3.1 基于DP屈服准则的坝基破坏分析模型
对于岩体材料,采用弹塑性模型,屈服准则采用DP(Drucker-Prager)屈服准则,即

式中α和k为材料参数,可以通过拟合摩尔-库伦准则得到.鉴于地应力场作用下的岩基为 3向受压区,采用压力子午线下的参数,在π平面上选用库伦六边形外接圆形式的DP准则,应用关联流动法则可以推导出

式中:c为黏聚力;ϕ为内摩擦角.
对于地基岩体,采用上述 DP屈服准则,考虑塑性屈服区扩展、联结,最后贯通,诱发其丧失承载能力.此时,便可以认为地基结构达到其承载极限,功能失效.失稳表达式为

式中;φ为屈服面;iA为局部屈服区φ∗组成的机构.
1.3.2 基于变形体突变的极限稳定性分析模型
坝基渐进破坏过程的分析让人易于理解,但不同的本构模型和破坏准则以及人为主观因素的影响会导致判别结果的精度[5],同时,考虑到地震荷载的往复特性和瞬态特性,加之材料非线性导致的应力转移现象,瞬时动力失稳尚不能说明坝体系统达到其极限抗震能力,因此,进一步从变形稳定的角度评判坝基是否达到其极限承载状态.
在非线性有限元计算过程中,如果施加在结构上的荷载临近极限荷载时,坝体坝基系统的某些特征点位移会发生突变,可据此判别系统是否达到其极限承载力[5].因此,本文以系统稳定状态突变导致非线性计算不收敛为判据,评估重力坝达到系统稳定状态极限时的抗震能力.
1.4 极限抗震能力综合研究方法
综合上述系统破坏判据及对破坏状态的界定,本文从数值仿真试验的角度,建议从重力坝系统的损伤破坏等级、坝体混凝土开裂破坏模式、坝基岩体破坏扩展规律、系统稳定性突变等方面综合评价重力坝的极限抗震能力.
(1) 指标 E1:基于 Ghanaat坝体安全评价理念和弹塑性损伤理论,分别从线弹性和弹塑性损伤分析的角度,定量反映重力坝系统的损伤破坏等级,初步评估大坝的极限抗震能力.
(2) 指标 E2:从坝体坝基系统破坏模式角度评价大坝极限抗震能力.重力坝的开裂破坏是一个逐渐累积、渐进破坏的过程,当开裂破坏使大坝出现渗漏或出现坝块脱落时,大坝将丧失正常挡水功能,大坝达到极限抗震能力.同时考虑混凝土和坝基岩体材料的非线性,通过计算不同等级强震作用下大坝的损伤、开裂破坏,将坝体贯穿性裂缝的出现以及坝基损伤屈服贯通性破坏作为系统动力失效、达到其极限抗震能力的表征.
(3) 指标 E3:从坝基动力极限承载能力角度评价大坝极限抗震能力.大坝沿坝基面及深层薄弱层面的稳定性是整个工程抗震设计的关键和安全评价的重要方面,在地震往复荷载作用下,坝体地基系统存在失稳的可能性.随着地震动强度的增大,当某些特征点位移发生突变时,表征坝体-坝基系统稳定性状态突变,非线性计算不收敛,系统达到其极限抗震能力.
最后,综合评价大坝极限抗震能力:基于上述分析结果,从系统功能失效风险的角度出发,综合坝体开裂破坏模式、坝基动力极限承载能力等方面,定义大坝的极限抗震能力为各个指标的最小值.
2 评价模型的验证
Koyna重力坝[15]作为少数几个在强震中破坏且有比较完整记录的重力坝之一,一直是混凝土坝动力分析的经典研究对象.Koyna混凝土重力坝坝高103,m,底宽 70.1,m,顶宽 14.78,m(见图 1).1967年12月11日,该坝坝址区域遭受一次6.5级强烈地震作用,在 91.7,m 高的库前水位、0.474g水平向与0.312g的竖向加速度峰值地震作用下,坝体发生开裂,并在裂缝处发生渗漏.已有许多学者对该坝的地震破坏过程进行了模拟分析.本文对 Koyna重力坝的极限抗震能力进行分析.

图1 Koyna大坝示意Fig.1 Sketch of Koyna dam
计算荷载考虑重力、静水压力、动水压力和Koyna地面实测地震波激励作用.坝体混凝土弹性模量[15]为31.0,GPa,泊松比为0.2,密度为 2,500,kg/m3,静态抗拉强度取 2.90,MPa;动水压力根据Westergaard公式考虑;阻尼比为0.05.采用动力超载法,分析Koyna大坝的极限抗震能力.
首先,按照指标E1对Koyna大坝进行极限抗震能力评价.由图 2可知,当输入基岩水平峰值加速度低于 0.400g时,大坝超应力累积持时均处于轻微破损区范围.当输入基岩峰值加速度大于等于 0.450g时,DCR=1的超应力累积持时大于0.3,s,且DCR=2的超应力累积持时大于 0,s,大坝处于严重损伤破坏区范围.因此,基于性能的抗震评价模型,初步认为Koyna重力坝的极限抗震能力为0.450g左右.

图2 基于功能的Koyna大坝抗震破坏等级评价Fig.2 Performance-based damage evaluation of Koyna dam
进一步根据指标 E2,分析坝体的潜在破坏模式.基于ANSYS弥散裂缝模型,图3给出了0.474g水平向实测地震波作用下的 Koyna大坝最终破坏模式与振动台模型试验[10]的结果.数值模拟得出的最终破坏形态与模型试验基本一致,也与 Koyna坝实际地震开裂位置吻合,说明基于弥散裂缝模型的破坏过程分析可以有效表达动力工况下混凝土开裂行为,能够很好地模拟地震荷载作用下坝体的强震破坏模式,评价大坝的极限抗震能力.由于缺乏Koyna大坝坝基动力破坏等相关实测资料,在不考虑坝基极限承载力条件下,认为 Koyna坝极限抗震能力为 0.450g左右,这与实际震害情况基本一致.

图3 数值计算破坏形态与模型试验结果比较Fig.3 Comparison of numerical failure mode and the model test
另外,笔者在文献[16]中,也从坝体开裂破坏、地震位移响应突变、塑性区贯通等方面对混凝土重力拱坝的极限抗震能力进行了初步探讨,这也佐证了文中评价模型对整体大坝和相似工程极限抗震能力评价的适用性.
3 工程实例分析
阿海水电站属一等大(1)型工程.拦河坝为混凝土重力坝,最大坝高为 138,m,水库正常蓄水位高程为 1 504,m.建基岩体主要为板岩砂岩互层结构,承载能力较好;工程区地震地质背景复杂,坝址区设计烈度接近Ⅸ度,其 100,a 超越概率 2%的基岩水平地震动峰值加速度达 0.344g.复杂层状岩基上的大坝抗震能力和抗震安全是本工程的关键技术问题.
3.1 数值模型及计算参数
4号溢流坝段结构体形突异,深层滑移模式复杂,是工程薄弱环节,需进行极限抗震能力分析.数值模型(见图 4)反映了坝段的主要结构特点、坝基岩体及主要地质构造分布,考虑板岩对大坝及地基应力的不利影响,通过适当的概化,对板岩单独划分单元,尽可能反映实际地质条件.
坝体混凝土采用弹塑性模型,失效面采用William-Warnke五参数强度准则;坝基岩体屈服面采用Mohr-Coulomb屈服面的外接圆锥.计算时大坝水位为正常蓄水位,动水压力根据 Westergaard公式考虑;Rayleigh阻尼因数根据线弹性分析得到的前两阶频率计算.模型材料参数见表 1.建基面(AB/BC/CD面)的内摩擦角和黏聚力分别为 38.66°和 0.61,MPa,深层 AC面的内摩擦角和黏聚力分别为 41.67°和0.80,MPa.

图4 溢流坝段(含滑动面)及三维离散模型Fig.4 Sketch of the overfall dam and its 3D discrete model

表1 坝体及地基材料力学参数Tab.1 Mechanical parameters of dam and foundation material
3.2 地震动输入及研究方案
坝区场地类别为Ⅰ类,100,a超越概率2%的基岩地震动水平向峰值加速度为 0.344g,100,a超越概率1%的基岩地震动水平向峰值加速度为 0.415g.基于有质量地基采用黏弹性人工边界输入,输入地震动按Koyna地震波(见图 5)调幅至不同强震等级,同时考虑水平向和竖向地震,竖向地震输入加速度峰值取为水平向的2/3.
为研究大坝的极限抗震能力,在设计地震(PGA为 0.344g)和校核地震(PGA为 0.415,g)的地震响应基础上,采用地震动超载法,又分别计算了基岩水平峰值加速度分别为 0.450g、0.500g、0.550g、0.600g等多个条件下的大坝动力响应.依据前述不同方面的指标,对大坝极限抗震能力进行综合评价.
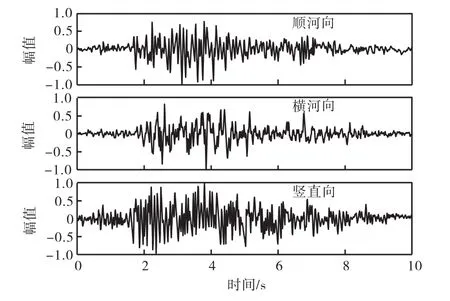
图5 Koyna波加速度时程归一化曲线Fig.5 Normalized curves of Koyna wave ground acceleration
3.3 从结构损伤破坏等级分析极限抗震能力
通过对各方案下坝体特征点动应力时程曲线对比,中墩与溢流堰顶的连接区域动力响应较大,是结构动力响应的控制性区域,该部位的破坏也将直接导致大坝蓄水功能的失效.因此将该部位的需求能力比和超应力累积持时作为控制指标.该区域混凝土动态名义抗拉强度达 4.789,MPa(DCR=2的分界点),图6给出了PGA为0.450g和0.500g时该部位的竖向正应力时程,进而得出需求能力比和超应力累积持时指标.根据文献[7]的计算方法,基于线弹性模型的不同等级地震作用下的大坝损伤破坏等级如图7所示.
当地震动峰值加速度增大至0.450g时,DCR=1的超应力累积持时达到了0.29,s(小于0.30,s),DCR=2超应力累积持时为 0,s,仍处于中低等损伤破坏区.继续增大至0.500g时,DCR=1的超应力累积持时大于 0.30,s,且 DCR=2的超应力累积持时大于0,s,坝体已处于严重损伤破坏范围内.
进一步,基于ABAQUS中的塑性损伤模型,对坝体动力损伤情况进行分析.选取大坝典型部位的单元,绘制结构动力非线性损伤演化情况,如图8所示.

图6 竖向最大拉应力Fig.6 Maximum vertical tensile stress
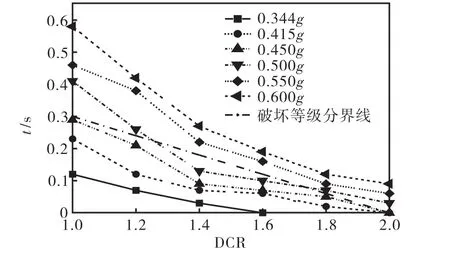
图7 基于功能的阿海大坝抗震破坏等级评价Fig.7 Performance-based seismic damage evaluation of Ahai gravity dam

图8 PGA=0.500g时坝体关键部位的损伤演化过程Fig.8 Damage evolution vs time when PGA=0.500g
由此可见,大坝首先在下游溢流导墙与闸墩交接处(E847)损伤开裂,随后是坝踵单元(E2347),接着是溢流面下游折坡(E10206)处,最后迎水面 1,469,m高程处上游坝面(E490)也逐渐损伤破坏直至出现裂缝.同时,在地震作用的前4,s内,坝体损伤较小且发展缓慢,地震峰值时刻后迅速发展,局部开裂已经完成.此后损伤变量接近稳定并维持在一定程度.
将中墩与溢流堰顶的连接区破损视为导致大坝蓄水功能失效的关键区域,结合基于性能的抗震评价模型,大坝的极限抗震能力指标 E1可初步评价为0.550g,此时大坝已处于严重损伤破坏,需进行大坝非线性分析,从坝体-坝基的潜在失效模式,进一步评估大坝-地基系统的极限抗震能力.
3.4 从坝体开裂破坏模式分析极限抗震能力
将混凝土作为连续介质,基于ANSYS软件中的弥散裂缝模型对坝体在不同强度地震动作用下的裂缝分布及开裂状态进行分析.
如图9所示,当PGA=0.415g时,坝踵回填混凝土基本裂穿,闸墩与溢流堰顶连接处出现水平张开裂缝,坝段主体结构受地震影响不大;PGA=0.450g的情况较 PGA=0.415g时并无明显恶化,当地震峰值增大至 0.500g时,闸墩两侧与溢流堰顶连接处出现几乎贯通堰顶的水平向闭合裂缝,建基面也出现多处裂缝,此时中墩结构破坏导致挡水功能失效的概率明显增大;进一步,当 PGA=0.550g时,溢流堰顶已经出现了贯通结构上下游方向的贯穿性裂缝.继续增大至 0.600g时,结构非线性计算不收敛.另外,数值仿真得到的坝体破坏模式与文献[3]中类似工程溢流坝段物理模型试验所得的大坝动力破坏形态相似,这也佐证了数值分析中坝体开裂破坏模型的适用性和正确性.

图9 不同强度地震作用下坝体裂缝分布规律Fig.9 Crack distribution under different earthquakes
从坝体开裂破坏模式指标 E2看,大坝的极限抗震能力为0.550g~0.600g.
3.5 从坝基极限承载能力分析极限抗震能力3.5.1 坝基渐进破坏规律分析
坝基地质特点决定地基塑性变形发展规律,地基塑性屈服可能会造成系统突变失稳,进而影响坝体系统的极限抗震能力.基于 ABAQUS分析平台,坝基岩体采用外接圆锥DP屈服准则,不同地震加速度下坝基塑性区分布如图10所示.PGA=0.415g时,坝基塑性区出现在坝踵区域且沿反倾节理方向延伸;当PGA=0.450g时,坝基塑性区沿坝基面向下游穿过帷幕范围,同时沿反倾节理进一步延伸,另外,坝趾处层间节理区域也开始出现塑性区;PGA=0.500g时,坝踵塑性区向深部扩展,坝趾处塑性区进一步沿层面节理延伸;PGA增大至0.550g时,坝踵处塑性区范围较 PGA=0.500g时并无显著增大,但塑性变形量值却显著增大.地震峰值加速度至0.600g,非线性计算不收敛.

图10 不同强度地震作用下坝基塑性区分布(Avg:100%,单位:m)Fig.10 Plastic zone distribution under different earthquakes(Avg:100%,unit:m)
3.5.2 大坝抗滑稳定安全性分析
同时考虑坝体坝基的材料非线性,按照现行抗震规范的承载能力极限状态表达式,结合基于有限元的刚体极限平衡法、矢量和积分的概念,建立动力抗滑稳定安全系数的计算公式为

式中iS为单元i在滑移面的面积,其余参数参见抗震规范. ()1Ft= 时坝体处于极限平衡状态, ()1Ft<时系统的瞬态稳定可靠性便得不到保证.各滑动模式的抗滑稳定安全系数最小值见表2.
由表2可知,随着基岩输入地震动峰值加速度的增大,坝基抗滑稳定安全系数不断减小,PGA=0.550g下的坝体已有个别时段的抗滑稳定安全系数小于1.0,当PGA=0.600g时,非线性计算不收敛.3.5.3 系统状态突变分析
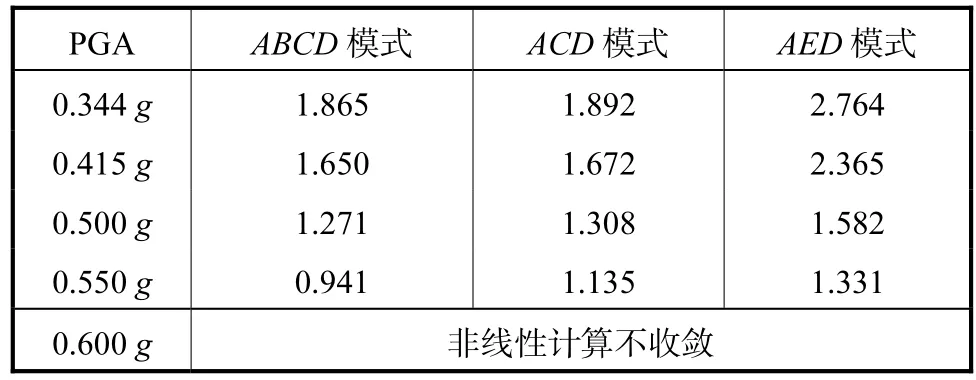
表2 多滑移模式的抗滑稳定安全系数最小值Tab.2 Minimum safety factors of different sliding modes
坝顶顺河向位移发展规律是判断坝体破坏的一个重要指标.PGA=0.550g时,坝顶顺水流向位移逐渐增大至 40,mm并在其上下波动,最大位移达到100,mm,如图 11所示,说明坝顶闸墩已经存在开裂并向下游倾倒趋势,但仍能保持一定的整体性;当PGA=0.600g时,坝顶顺水流位移在4.45,s后发生明显突变,系统失稳,非线性计算不收敛,可认为坝体系统破坏.
因此,结合坝基渐进破坏规律、系统抗滑稳定和状态突变情况,从坝基极限承载能力方面看,初步认为,大坝的极限抗震能力为0.550g~0.600g.

图11 坝顶顺水流方向位移时程曲线Fig.11 Displacement curves along the flow at the crest dam
3.6 大坝极限抗震能力的综合评价
基于上述计算结果,从坝体损伤破坏等级、开裂破坏模式,坝基岩体渐进破坏规律,系统抗滑稳定和状态突变等多个指标综合评价,坝体的极限抗震能力为 0.550g~0.600g.
需要说明的是,考虑坝段间相互作用的整体大坝三维效应、固结灌浆、帷幕失效等都可能影响大坝的极限抗震能力.鉴于问题的复杂性,本文仅是从数值模型试验的角度,对混凝土重力坝的极限抗震能力的评价方法进行初步探讨,要达到成熟完善,还有待于对大量实际工程的校准分析及物理模型试验的验证.今后宜结合实际震害资料和模型试验等进行深入探讨和研究.
4 结 论
重力坝的极限抗震能力,目前还没有统一的评价标准可以参照,需从多种角度进行综合分析.鉴于模型试验本身存在一定的缺陷,无法考虑诸如地基和混凝土的各向异性等因素的影响,宜结合数值仿真方法,分析大坝系统破坏的全过程力学行为,将结构的强度判据和稳定判据统一起来,综合评价重力坝的极限抗震能力.
(1) 极限地震荷载下的系统功能失效是重力坝达到极限抗震能力的重要表征.基于数值试验的极限抗震能力综合评估方法,从结构系统的潜在失效模式出发,在系统分析极端地震荷载下坝体坝基关键性能的基础上,对重力坝极限抗震性能进行了综合评价,避免了单一收敛性或系统突变评价准则的缺陷.
(2) 基于数值试验结果,从重力坝系统的损伤破坏等级、坝体混凝土开裂破坏模式、坝基岩体塑性破坏扩展规律、系统抗滑稳定和状态突变情况等方面综合评价,初步认为阿海大坝溢流坝段极限抗震能力为0.550,g~0.600,g.
(3) 数值仿真分析中,地震动输入模型始终不能避免与实际地震动激励之间的区别,因而也会造成极限抗震能力的差别:一是复杂的地基特性对地震波传播过程有较大影响,二是地震动的输入方式和入射角度等都会对结构的动力响应和极限抗震能力产生影响.因此,研究地震波斜入射条件下的重力坝极限抗震能力是进一步工作的方向.
[1] Hinks J L,Gosschalk E M. Dam and earthquake [J].Dam Eng,1993,4(1):9-24.
[2] Shen Chonggang,Chen Houqun,Zhang Chuhan,et al. Earthquakes induced by reservoir impounding and their effect on Hsingfengkiang dam [J]. Scientia Sinica,1974,17(2):239-272.
[3] 范书立,陈健云,周 晶,等. 龙开口水电站溢流坝段动力模型破坏试验研究[J]. 水利学报,2007,38(增):195-199.Fan Shuli,Chen Jianyun,Zhou Jing,et al. Experimental research on overfall section dynamic rupture of Longkaikou project [J]. Journal of Hydraulic Engineering,2007,38(Suppl):195-199(in Chinese).
[4] 李 昇,张社荣,贾 璐,等. 强震作用下混凝土重力坝破坏模式研究[J]. 水利水电技术,2010,41(2):22-26.Li Sheng,Zhang Sherong,Jia Lu,et al. Study on failure mode for concrete gravity dam under impact of strong earthquake [J]. Water Conservancy and Hydropower Technology,2010,41(2):22-26(in Chinese).
[5] 周 伟,常晓林. 高混凝土重力坝复杂坝基稳定安全度及极限承载能力研究[J]. 岩土力学,2006(增 1):161-166.Zhou Wei,Chang Xiaolin. Study of stabilization safety and limit load carrying capacity for complex foundation of high concrete gravity dam [J]. Rock and Soil Mechanics,2006(Suppl 1):161-166(in Chinese).
[6] Ghanaat Y. Failure modes approach to safety evaluation of dams [C] //13th World Conf on Earthquake Eng. Canada,2004:1115-1-15.
[7] 沈怀至,张楚汉,寇立夯. 基于功能的混凝土重力坝地震破坏评价模型[J]. 清华大学学报:自然科学版,2007,47(12):29-32.Shen Huaizhi,Zhang Chuhan,Kou Lihang. Performance-based seismic damage assessment model of concrete gravity dams[J]. Journal of Tsinghua University:Science and Technology,2007,47(12):29-32(in Chinese).
[8] Pekau O A,Cui Yuzhu.Failure analysis of fractured dams during earthquakes by DEM[J]. Engineering Structures,2004,26(10):1483-1502.
[9] 张楚汉,王光纶. 水利水电工程科学前沿[M]. 北京:清华大学出版社,2002.Zhang Chuhan,Wang Guanglun. Frontier Problems of Water Conservancy and Hydropower Engineering[M].Beijing:Tsinghua University Press,2002(in Chinese).
[10] Lee J,Fenves G L. A plastic-damage concrete model for earthquake analysis of dams [J]. Earthquake Engineering and Structural Dynamics,1998,127(9):937-956.
[11] William K J,Warnke E P. Constitutive model for the triaxial behavior of concrete[C]//Proceedings of International Association for Bridge and Structural Engineering.Bergamo:ISMES,1975:1-30.
[12] 沈怀至,周元德,王进廷. 基于弥散裂缝模型的重力坝简化地震分析[J]. 水利学报,2007,38(10):1221-1227.Shen Huaizhi,Zhou Yuande,Wang Jinting. Simplified earthquake analysis of concrete gravity dams using smeared crack approach [J]. Journal of Hydraulic Engineering,2007,38(10):1221-1227(in Chinese).
[13] Hilleborg A,Modeer M,Petersson P E. Analysis of crack of formation and crack growth in concrete by means of fracture mechanics and finite elements [J].Cement and Concrete Research,1976,6(6):773-782.
[14] de Borst R. Fracture in quasi-brittle materials:A review of continuum damage-based approaches[J]. Engineering Fracture Mechanics,2002,69(2):95-112.
[15] Chopra A K,Chakrabarti P. The Koyna earthquake and the damage to Koyna dam[J]. Bull Seism Soc Am,1973,63(2):381-397.
[16] 张社荣,王高辉,王 超. 混凝土重力拱坝极限抗震能力评价方法初探[J]. 四川大学学报:工程科学版,2012,44(1):7-12.Zhang Sherong,Wang Gaohui,Wang Chao. Preliminary study on the ultimate seismic capacity evaluation of concrete gravity arch dam[J]. Journal of Sichuan University:Engineering Science Edition,2012,44(1):7-12(in Chinese).
