环Fq＋uFq＋u2Fq上任意长度的循环码

胡 庆， 李 平

（合肥工业大学 数学学院，安徽 合肥 230009）

环Fq＋uFq＋u2Fq上任意长度的循环码

胡 庆， 李 平

（合肥工业大学 数学学院，安徽 合肥 230009）

文章根据环Fq＋uFq上循环码结构，研究了Fq＋uFq＋u2Fq上的任意长度的循环码，同时研究了Fq＋uFq＋u2Fq上的这些循环码的秩和最小生成元集。

环同态；循环码；对偶码；秩

多项式剩余类环的结构介于有限域和环之间，因其具有良好的性质，其上的纠错码理论研究也备受关注。文献［1］研究了Z4上长度为2e的循环码；文献［2］讨论了环F2＋uF2上奇长度的循环码及自对偶码；文献［3］给出了环F2＋uF2上长为2n的循环码的计数；文献［4－5］给出了环z2＋uz2和z2＋uz2＋u2z2上任意长度的循环码的结构及其重量；文献［6］给出了环Fq＋uFp＋…＋uk－1Fp上单根循环码以及自对偶码的结构；文献［7］研究了环F2＋uF2上长度为2e的循环码；文献［8－9］用相同的方法研究了当码长n和有限链环的特征p互素时，循环码的结构。

本文基于环Fq＋uFq上任意长度的循环码结构及其对偶码［10］，给出了环Fq＋uFq＋u2Fq上任意长度的循环码结构。

令R为任意一个幺环，R上的长为n的线性码是Rn的R－子模。C为R上长为n的线性码，若∀（c0，c1，…，cn－1）∈C，有（cn－1，c0，…，cn－2）∈C，则称C为循环码。可以把R上长为n的循环码看成是R［x］／〈xn－1〉的理想。令u＝（u0，u1，…，un－1），v＝（v0，v1，…，vn－1）为环R上任意2个长为n的向量，定义这2个向量的内积为u·v＝u0v0＋u1v1＋…＋un－1vn－1。若u·v＝0，则称u与v正交。循环码C的对偶码为集合C⊥＝｛u∈Rn：u·v＝0，∀v∈C｝。显然C⊥也是循环码，循环码C的所有码字的多项式集合记为P（C），则｛P（C），＋，·｝是R［x］／（xn－1）的理想。将任一码字等同它的多项式表示，则R上长为n的循环码即R［x］／（xn－1）的理想，P（C）也称为循环码C的对应理想。

定义1 令I为环Rn的一个理想，定义A（I）＝｛g（x）∈Rn：f（x）g（x）＝0，∀f（x）∈I｝，称A（I）为I的零化子。

定义2 设f（x）＝a0＋a1x＋…＋arxr是r次多项式，记f＊（x）＝ar＋ar－1x＋…＋a0xr，称为f（x）的互反多项式。

易证，若循环码C的对应理想为I，则对偶码C⊥的对应理想为A（I）＝｛f＊（x）：∀f（x）∈I｝。

1 环R和S上的循环码的生成子

令C为环S上长为n的循环码，定义ψ1：S→R，ψ1（c），ψ1是环同态，所以可以扩展成同态φ1：C→Rn，定义为：

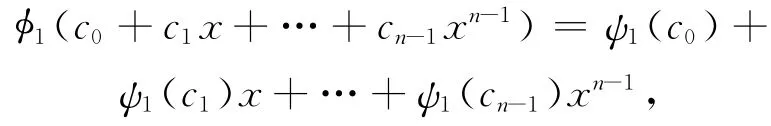
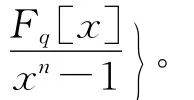
令D为Rn＝R［x］／（xn－1）的理想，定义ψ2：R→Fq，ψ2（a0＋ua1）＝（a0＋ua1）q＝＋＝＝a0，且a0，a1∈Fq。则ψ2是R到Fq的环同态，把ψ2扩展成Rn到Fq［x］／（xn－1）的环同态φ2，将φ2限制在D上所得φ2｜D不引起混淆时，仍记成φ2，φ2：D→Fq［x］／（xn－1），φ2（c0＋c1x＋ … ＋cn－1xn－1）＝ψ2（c0）＋ψ2（c1）x＋…＋ψ2（cn－1）xn－1，kerφ2＝ ｛ur（x）：r（x）∈Fq［x］／（xn－1）｝＝ua1（x），其中a1（x）｜（xn－1）modp。则可得φ2的象为Fq［x］／的理想，所以应为Fq上的循环码，即φ2的象由g（x）生成，其中g（x）∈Fq［x］／（xn－1），且g（x）｜（xn－1）。所以D＝（g（x）＋up（x），ua1（x）），其 中p（x）∈Fq［x］。 因 为，可以推出up同理，由ug∈kerφ1可得a1｜g。

引理1 设C是R上长为n的循环码，存在唯一满足a（x）｜g（x）｜xn－1，dega（x）＞degp（x）的Fq［x］中多项式g（x）、a（x）、p（x），使C＝（g（x）＋up（x），ua（x）），且kerφ2＝（ua（x））。

引理2 设C为R上循环码，C＝（g（x）＋up（x），ua（x）），若g（x）＝a（x），degg（x）＝r，则C＝（g（x）＋up（x）），且 在R中 （g＋up）｜（xn－1）。

证明 因为u（g＋up）＝ug且g＝a，则显然C⊂（g＋up），又因为（g＋up）⊂C，所以C＝（g＋up）。由带余除法得xn－1＝（g＋up）q＋t，其中t＝0或者deg＜r。因为t∈C，则t＝0，因此在Fq＋uFq中（g＋up）｜（xn－1）。

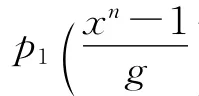
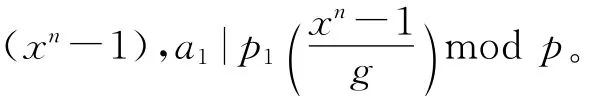
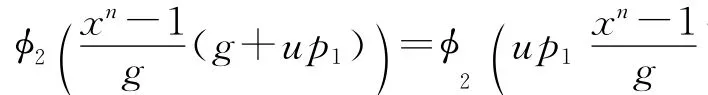
引理4 在引理3中，degp2＜dega2，degq1＜dega2，degp1＜dega1。

证明 根据结论，若C＝（a，b），则对于任意的d都有C＝（a，b＋dc）。

引理5 若C为环S上的循环码，则可唯一地写成C＝ （g＋up1＋u2p2，ua1＋u2q1，u2a2）。

证明 假设C＝（g＋up1＋u2p2，ua1＋u2q1，u2a2）＝（h＋um1＋u2m2，ub1＋u2l1，u2b2），因为kerφ1＝（u2a2）＝（u2b2），则a2＝b2。同理，因为kerφ2＝（ua1）＝（ub1），可得a1＝b1。又因为φ2（φ1（C））＝（g）＝（h），故g＝h。因为g＋up1＋u2p2∈C＝（g＋um1＋u2m2，ua1＋u2l1，u2a2），则g＋up1＋u2p2＝g＋um1＋u2m2＋α1（ua1＋u2l1）＋α2（u2a2），两边同时乘以u，可得u2p1＝u2m1＋α1（u2a1），推出u2（p1－m1）＝u2α1a1，因为deg（p1－m1）＜degb1，所以p1＝m1。由以上证明可得u2p2＝u2m2＋（ua1＋u2l1）α1＋u2a2α2⇒u2（p2－m2）＝（ua1＋u2l1）α1＋u2a2α2，则u2（p2－m2）∈C。故u2（p2－m2）∈kerφ2＝（u2a2（x））。但是deg（p2－m2）＜dega2，就有p2＝m2。类似地，可以推出q1＝l1，则循环码可以唯一写成C＝（g＋up1＋u2p2，ua1＋u2q1，u2a2）。

引理6 若C＝（g＋up1＋u2p2，ua1＋u2q1，u2a2）为S上的循环码，且a2＝g，则C＝（g＋up1＋u2p2），其中（g＋up1＋u2p2）｜（xn－1）。

证明 参考引理2的证明。

引理7 若C为S上长为n的循环码，n与p互素，则C＝（g，ua1，u2a2）＝ （g＋ua1＋u2a2）。

证明 因为n与p互素，所以（xn－1）可以分解为互异的不可约多项式的乘积形式，可以得到：

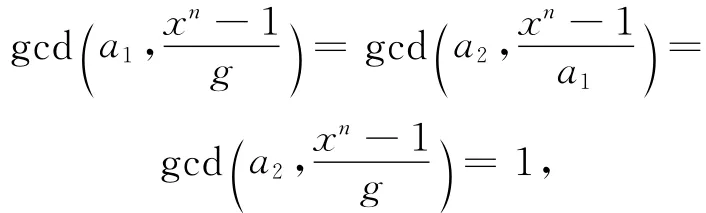
引理8 令C为R上长为n的循环码，u2＝0，modp。

（1）若n与p互素，则Rn是主理想环，C＝（g，ua）＝（g＋ua），其中g和a为Fq上的多项式，且a｜g｜（xn－1）modp。

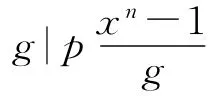
定理1 令D为S上长为n的循环码，u3＝0modp，有以下情形。

（1）若n与p互素，则Sn为主理想环，D＝（g，ua1，u2a2）＝（g＋ua1＋u2a2），g（x）、a1（x）和a2（x）为Fq上的多项式，a2（x）｜a1（x）｜g（x）｜（xn－1）modp。

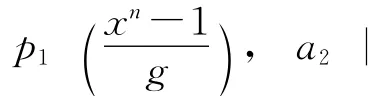
证明 （1）见引理3及引理7。

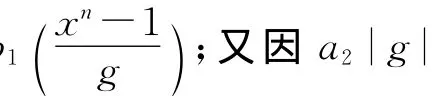
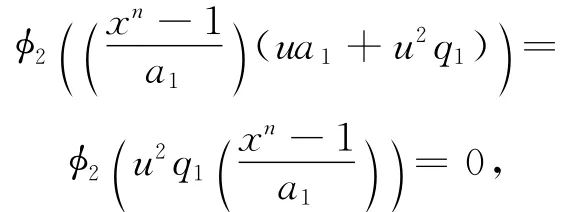
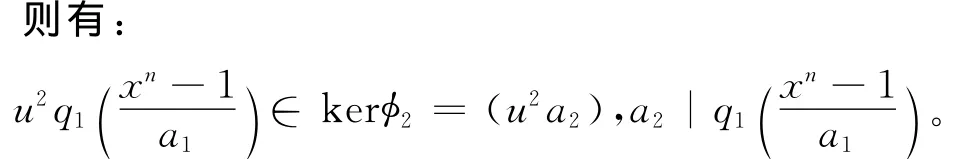
2 循环码的秩和对偶码

引理9 令C为环R＝Fq＋uFq上长为n的循环码，其中n与环R的特征p不互素。

（1）若C＝（g（x）＋up（x）），deg（g（x）＋up（x））＝r，（g（x）＋up（x））｜（xn－1），则C是自由模，且rank（C）＝n－r，则基为β1＝｛g（x）＋up（x），x（g（x）＋up（x）），…，xn－r－1（g（x）＋up（x））｝，｜C｜＝q2n－2r。

（2）若C＝ （g（x）＋up（x），ua（x）），其中degg（x）＝r，dega（x）＝t。则rank（C）＝n－t，C的最小生成集合可以写成：

β2＝｛g（x）＋up（x），x（g（x）＋up（x）），…，xn－r－1（g（x）＋up（x）），ua（x），xua（x），…，xr－t－1ua（x）｝，｜C｜＝q2n－r－t。

引理10 设C为R上长为n的循环码，p为环R的特征，n与p不互素，则有：

（1）若C＝（g（x）＋up（x）），deg（g（x）＋up（x））＝r，（xn－1）＝（g（x）＋up（x））（h（x）＋uq（x）），则A（C）＝ （h（x）＋uq（x）），C⊥＝（（h（x）＋uq（x）＊）。

定理2 令C为Fq＋uFq＋u2Fq上的长为n的循环码，u3＝0modp，且n与p互素，有以下情形。

（1）若C＝（g＋up1＋u2p2），deg（g＋up1＋u2p2）＝r，则C是秩为n－r的自由模，基为β1＝｛（g＋up1＋u2p2），x（g＋up1＋u2p2），…，xn－r－1（g＋up1＋u2p2）｝。

（2）令C＝（g＋up1＋u2p2，ua1＋u2q1，u2a2），deg（g＋up1＋u2p2）＝r，deg（ua1＋u2q1）＝s，且degu2a2＝t，则C的秩为n－t，最小生成集为：

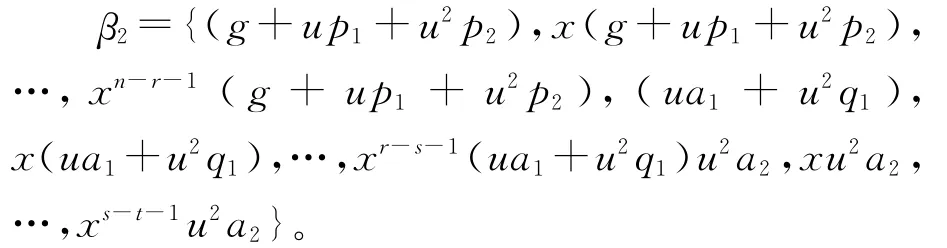
（3）若C＝（g＋up1＋u2p2，u2a2），deg（g＋up1＋u2p2）＝r，degu2a2＝t，则rank（C）＝n－t，最小生成集为：

证明 （1）在S＝Fq＋uFq＋u2Fq上，有

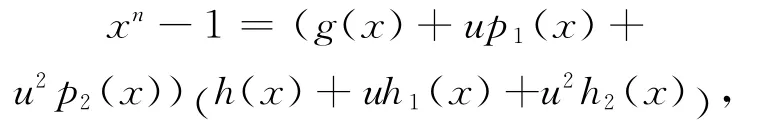
令c（x）∈C＝（g（x）＋up1（x）＋u2p2（x）），则

c（x）＝ （g（x）＋up1（x）＋u2p2（x））f（x），其 中，f（x）∈ （Fq＋uFq＋u2Fq）［x］，若degf（x）≤n－r－1，则c（x）可以写成β1的线性组合形式。

由带余除法可得存在多项式q（x）与r（x），使得

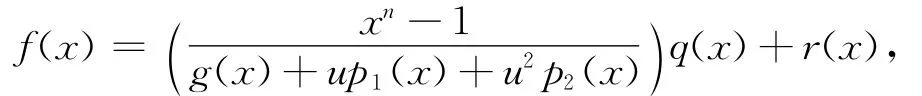
其中，r（x）＝0或者degr（x）≤n－r－1，即

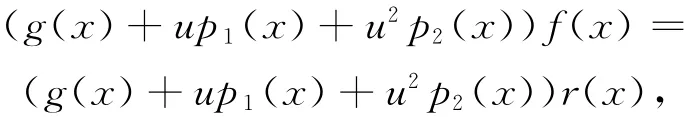
所以β1生成C。

现在只要证明β1线性无关即可。令

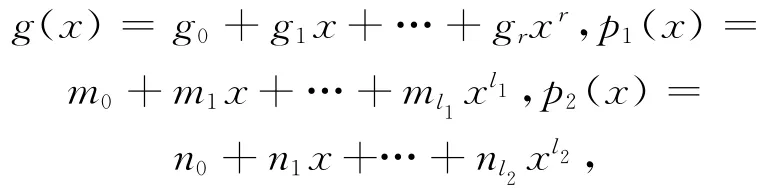
其中，g0∈，gi，mj，nk∈Fq，1≤i≤r，0≤j≤l1，0≤k≤l2。可设

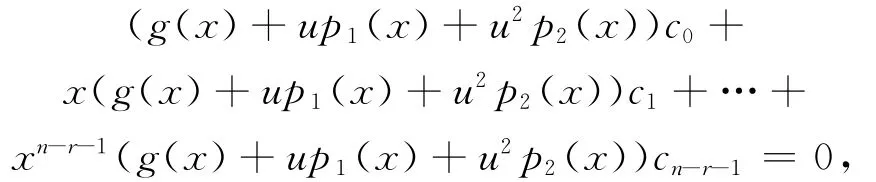
比较系数，可得（g0＋um0＋u2n0）c0＝0。因为（g0＋um0＋u2n0）为单位，故有c0＝0。因此有：

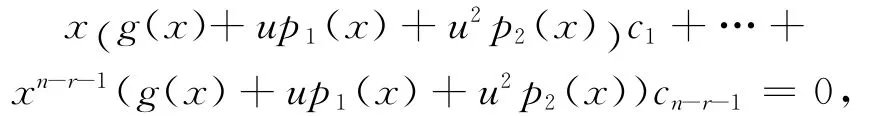
对比x的系数，有（g0＋um0＋u2n0）c1＝0，所以c1＝0。依此类推，ci＝0，i＝0，1…，n－r－1，因此β1为线性无关，且是C的生成集合。

（2）若C＝ （g（x）＋up1（x）＋u2p2（x），ua1（x） ＋u2q1（x），u2a2（x））， 其 中，deg （g（x）＋up1（x）＋u2p2（x））＝r，deg（ua1（x）＋u2q1（x））＝s，deg（u2a2（x））＝t，则在C中次数最低的多项式是u2a2（x）。可知β2生成

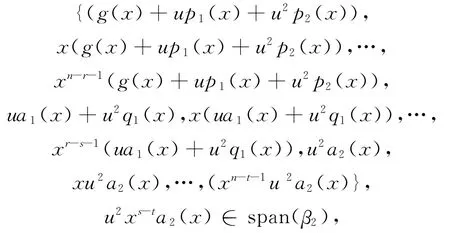
令xs－ta2（x）的 系 数 为a0，g（x）＋up1（x）＋u2p2（x）的系数为g0，则存在c0∈Fq，使a0＝c0g0，即

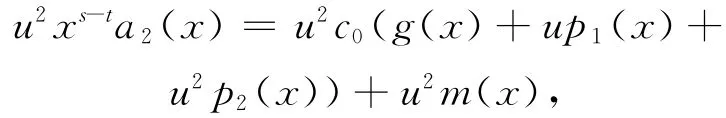
其中u2m（x）为C中次数小于t的多项式。因为C中所有多项式次数都不小于deg（u2a2（x））＝t，因此s≤deg（m（x））≤t，且

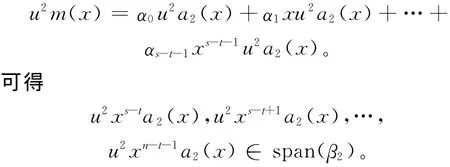
则β2是个生成集，参考证明（1），比较系数，可得β2线性无关，所以β2为最小生成集合。

（3）参考（2）的证明。

3 举 例

在环F4＋uF4＋u2F4上的长度n＝5的循环码，有

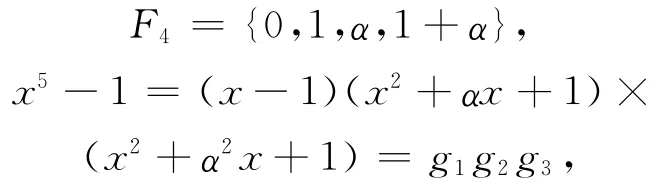
则F4＋uF4＋u2F4上长为5的非零循环码的生成子多项式如下：

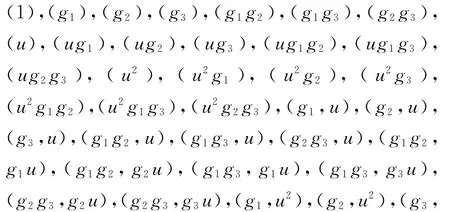
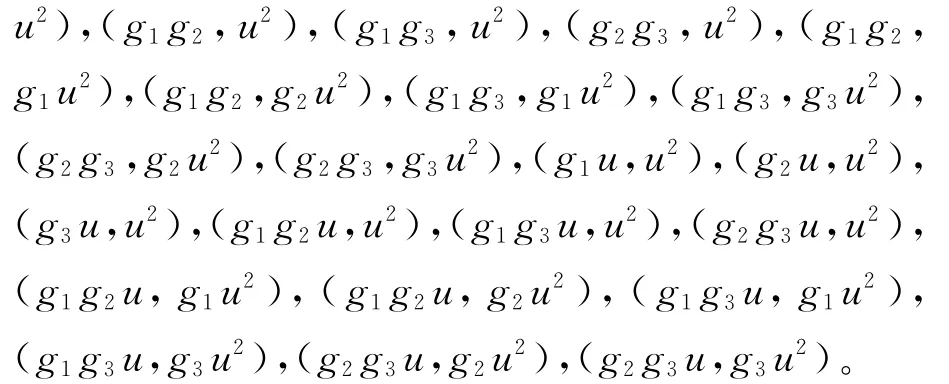
4 结束语

本文通过2个映射，从环Fq和Fq＋uFq上循环码的结构，给出了环S＝Fq＋uFq＋u2Fq上任意长度的循环码的结构。下一步将尝试讨论环S上循环码的对偶码的结构，以及Fq＋uFq和Fq＋uFq＋u2Fq上循环码的距离和重量。

［1］Abualrub T，Oehmke R.On the generators ofZ4cyclic codes of length 2e［J］.IEEE Trans Inf Theory，2003，49（9）：2126－2133.

［2］Bonnecaze A，Udaya P.Cyclic codes and self－dual codes overF2＋uF2［J］.IEEE Trans Inf Theory，1999，45（4）：1250－1255.

［3］王冬银，朱士信.环F2＋uF2上长度为2n（n为奇数）的循环码的个数［J］.合肥工业大学学报：自然科学版，2006，29（11）：1470－1472.

［4］Abualrub T，Siap I.On the construction of cyclic codes over the ringZ2＋uZ2［C］／／Proceedings of the 9th WSEAS International Conference on Applied Mathematics，Istanbul，Turkey，2006：430－435.

［5］Abualr T，Siap I.Cyclic codes over the ringsZ2＋uZ2andZ2＋uZ2＋u2Z2［J］.Designs Codes and Cryptography，2007，42（3）：273－287.

［6］Qian J F，Zhang L N，Zhu S X.Cyclic codes overFp＋uFp＋…＋uk－1Fp［J］.IEICE Transactions on Fundamentals，2005，E88－A（3）：795－797.

［7］李 平，朱士信.环F2＋uF2上长为2e的循环码［J］.电子与信息学报，2007，29（5）：1124－1126.

［8］Dinh H Q，Lopez－Permouth S K.Cyclic and negacyclic codes over finite chain rings［J］.IEEE Trans Inf Theroy，2004，50（8）：1728－1744.

［9］李光松，韩文报.有限链环上的循环码及其Mattson－Solomn多项式［J］.高校应用数学学报：A 辑，2004，19（2）：127－134.

［10］李 平，朱士信.环Fq＋uFq上任意长度循环码［J］.中国科学技术大学学报，2008，38（12）：1392－1396.

Cyclic codes of arbitrary lengths over the ringFq＋uFq＋u2Fq

HU Qing， LI Ping
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

According to the structure of the cyclic codes over the ringFq＋uFq，the cyclic codes of arbitrary lengths over the ringFq＋uFq＋u2Fqare analyzed.The rank and the minimal spanning sets of these cyclic codes over the ringFq＋uFq＋u2Fqare studied as well.

ring homomorphism；cyclic code；dual code；rank

TN911.22

A

1003－5060（2013）02－0243－05

10.3969／j.issn.1003－5060.2013.02.024

2012－08－30

国家自然科学基金资助项目（60973125）；合肥工业大学博士学位人员专项基金资助项目（2010HGBZ0550）和合肥工业大学青年教师创新基金资助项目（2011HGQC1023）

胡 庆（1988－），女，安徽亳州人，合肥工业大学硕士生；

李 平（1971－），男，安徽巢湖人，博士，合肥工业大学副教授，硕士生导师.

（责任编辑 吕 杰）