基于两货栈和延期支付的零售商最优订货和支付策略

杨爱峰， 杨晓琴， 胡小建

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.合肥工业大学 过程优化与智能决策教育部重点实验室，安徽 合肥 230039）

基于两货栈和延期支付的零售商最优订货和支付策略

杨爱峰1，2， 杨晓琴1，2， 胡小建1，2

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.合肥工业大学 过程优化与智能决策教育部重点实验室，安徽 合肥 230039）

文章假设供应商给零售商一个延期支付期限，零售商可以选择3种支付货款方式，在不同的支付方式下通过对利息收益和利息支出等关键指标的计算，分别建立了两货栈的库存模型；通过对模型的分析和求解，得出各种支付方式下的最小周期和最小成本，零售商可以根据所得结果来判断应该采取哪种支付方式，以及在最优支付方式下采取的最优订货策略；最后通过算例对模型进行了验证，所得结果与实际相符合。

延期支付；两货栈；支付方式；库存；最优订货

很多库存模型只考虑单个货栈而且都假定该货栈具有无限的容量，这显然与实际不符，因为在现实中任何货栈的容量都是有限的。同时由于多种复杂因素的存在，零售商需要存放的物品数量超出其自有货栈容量，在此情况下零售商需考虑是租用货栈还是再建货栈以满足存储的需要，通常再建货栈的费用大于租用货栈的费用，为节约成本很多零售商采用了两货栈库存系统，一个是自有仓库（OW），另一个是租用仓库（RW），因此理论界不断地研究两货栈系统模型。文献［1］首先提出了两货栈的库存模型，确定了最优订货量的算法；文献［2］进一步研究了允许短缺的变质性物品的两货栈模型；文献［3］在文献［2］的基础上提出了两货栈生产批量模型；文献［4］研究了产品在变质情况下零售商的EOQ订货模型；文献［5－6］对需求随时间而变化的物品，通过考虑价格折扣而将两货栈系统作了进一步扩展；文献［7］在通货膨胀和允许短缺的条件下讨论了变质性物品的两货栈系统。

传统的交易模式中，总是一手交钱一手交货，但是供应商为了激励零售商的购买行为，通常会采取延期支付策略，即供应商给予零售商一个延期支付期限（记为M），在延期支付期限内，零售商可以积累其销售收入来获得额外的收益，若超出延期支付期限，零售商需要为库存产品占用的资金支付利息。文献［7－10］在允许购买费用滞后支付的条件下，构造了一系列变质性物品的两货栈库存模型，都是假设零售商在延期支付期限结束时支付所有货款，没有分析多种支付方式的最优策略。另外不少学者针对单货栈研究了最优支付方式，文献［11］在基本EOQ模型基础上研究了延期支付期限与订货周期之间的最优支付时间；文献［12－13］在物品变质和通货膨胀的前提条件下研究了零售商的最优支付时间；文献［14］研究了单货栈中2种支付方式的最优订货模型。

本文在前人研究成果的基础上，根据实际情况假设零售商有3种支付货款的方式：支付方式1，零售商不在M时刻支付货款，保持销售收入及利息到订货周期结束T时刻支付所有货款；支付方式2，零售商选择在M时刻支付部分货款，剩余货款在T时刻支付（其中部分货款包括到M时刻为止所售产品的销售收入及其利息收入2部分）；支付方式3，零售商选择在M时刻支付部分货款，M时刻后零售商实时地用所售产品的销售收入支付剩余货款，直至支付完毕。本文在两货栈条件下分别讨论了每种支付方式下零售商的利息收入和利息支出，从而确定了零售商订货的最佳周期和最小成本，因此零售商可以根据所得结果判断采取哪种支付方式，在最优支付方式下零售商将采用最优库存策略。

1 模型所用的符号和假设

本文模型所用的符号如下：D为年需求率；P为年补货率，且P＞D；A为零售商每次订货的固定费用；M为供应商给予零售商的延期支付期限；s为单位产品的销售价格；c为单位产品的采购成本；Ie为单位时间销售收入获得的利息收益；Ic为单位库存单位时间的利息支出；t1为补货结束时刻；t2为RW中货物销售完的时间；OW为自有货栈，其库存量为W；RW为租用货栈，其容量为无限；T为补货周期（决策变量）；Q为周期内总订货量；ho、hr分别为OW、RW中单位商品单位时间的库存保管费用，且hr≥ho；I1（t）为RW、OW中补货期t时刻的库存水平，0≤t≤t1；I2（t）为OW、RW中非补货期t时刻的库存水平，t1≤t≤T；TC（T）为年总成本。

模型的主要假设如下：① 只考虑一种产品，且不允许缺货；② 年需求率D为常数；③s＞c，Ic＞Ie，cIc＞sIe；④ 时间区间是无限的；⑤ 两货栈RW和OW的补货时间是相同的，且几乎为同时进行（即忽略从OW到RW的运输时间和费用），补货时先将货物存储在OW中，当库存量达到容量W时，再向RW补货，直到补货完成；在销售货物时，先销售RW中的货物，销售完后再销售OW中的货物；⑥ 本文不讨论在［0，t1］期间的货款支付，即M＞t1。

2 模型建立

基于以上假设和分析，当Q≤W时，零售商不需要另外租用货栈RW，所订购货物可以全部存放在自有货栈OW中，此时两货栈的库存变化情况与单货栈的库存变化情况相同，因此将此库存模型作为单货栈的特殊情况，参见文献［14］。

当Q＞W时，根据OW、RW两货栈库存的变化情况可分为0≤t≤t1、t1≤t≤t2和t2≤t≤T3个阶段来讨论，如图1所示。

图1 当Q＞W时，RW和OW的库存变化情况

在0≤t≤t1期间，即当库存水平将为0时，补货立即开始，在补货期间库存水平将以速率P－D增加，直到t＝t1时零售商的库存量达到最大时停止补货；在t1≤t≤t2期间，销售RW中的货物，在t2时刻RW中库存变为0；在t2≤t≤T期间，销售OW中的货物，直到OW中库存变为0。因此它们的库存变化如下：

对（1）式、（2）式分别求解得：

因库存水平在t1、t2点满足连续性，由（3）式、（4）式可得以下等式：

分别求解可得t1＝DT／P，t2＝T－W／D。

本文的最终目标是求得零售商的最小订货周期和最小成本，结合模型的分析，零售商在一个订货周期内的成本函数为：

其中

年库存费用＝RW库存费用＋OW库存费用＝

年利息支出与年利息收益的数值依赖于零售商采用的支付方式。

2.1 支付方式1

（1）当T≤M时，零售商不需要给供应商支付利息，只有利息收入，如图2所示。

年利息支出＝0，年利息收益＝sIe［Dtdt＋DTdt］／T＝sIeD（M－T／2）。

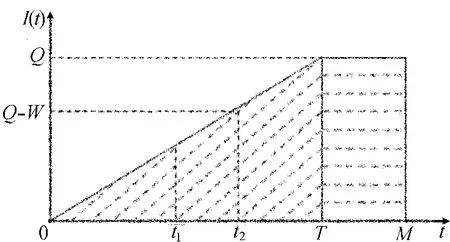
图2 当T≤M时的利息收益变化

（2）当T≥M≥t2时，零售商在M时刻之前只有利息收益，在M时刻之后便有利息支出，由于剩余货款选择在T时刻支付，在M和T之间零售商依然可以获得利息收益，如图3所示。

图3中实线部分表示利息支出变化情况，虚线部分表示利息收益变化情况。

图3 当T≥M≥t2时的利息支出与利息收益变化

（3）当T＞t2≥M≥t1时，同样零售商可以在T之前获得利息收益，在M时刻之后支付利息，如图4所示，图4中实线部分表示利息支出变化情况，虚线部分表示利息收益变化情况，由于RW和OW的库存变化不同，所以此期间的利息变化与T≥M≥t2期间的利息变化是不同的。

图4 当T＞t2≥M≥t1时的利息支出与利息收益变化

因此，零售商的总成本函数可总结为：

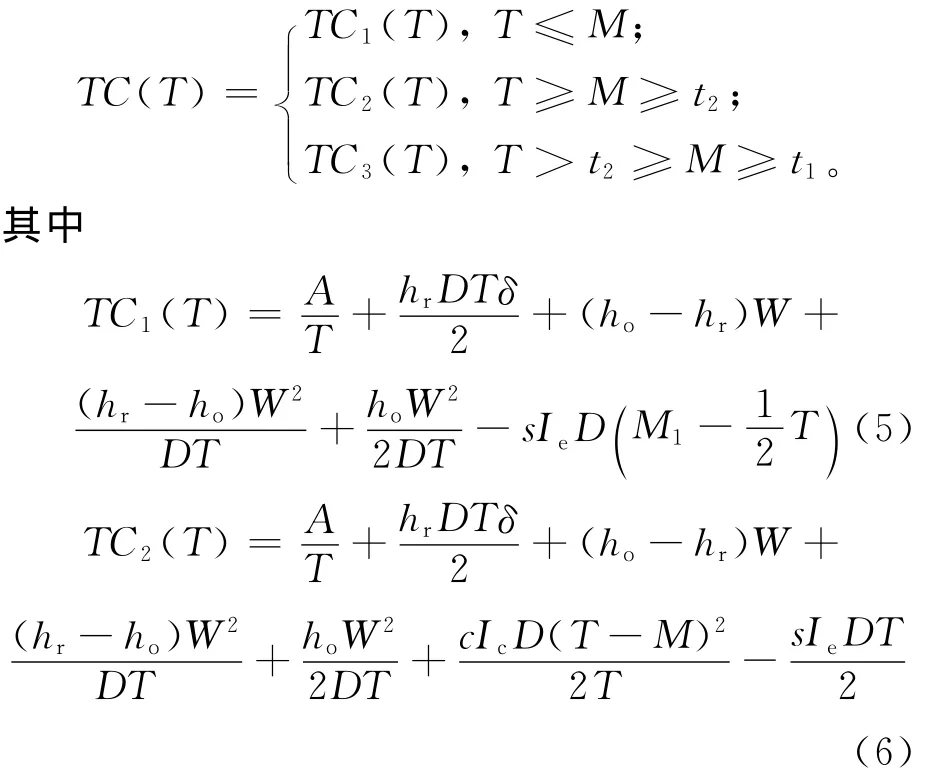
2.2 支付方式2

当T≤M时，零售商的利息支出和利息收益与第1种支付方式相同，因此略；当T≥M时，零售商将选择在M点支付部分货款，即M时刻前已销售所得收入及其利息收入之和，即部分货款＝sDM＋sIeDM2／2。

图5 当cQ－sDM－sIeDM2／2≤0时的利息收益变化

（2）如果零售商在M时刻的所有销售收入及其利息收入不能还清所有货款，在M时刻将用其已有的所有收入支付部分货款，剩余货款在T时刻支付，那么在M到T时刻，零售商还有部分的利息支出，同时还可以重新获得部分利息收入，如图6所示。

图6 当cQ－sDM－sIeDM2／2＞0时利息支出与利息收益变化

图6中实线部分表示利息支出变化情况，虚线部分表示利息收益变化情况。即当cQ－sDM－sIeDM2／2＞0时，有

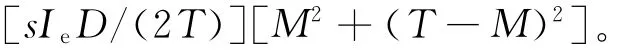
因此，零售商的总成本函数可总结为：

2.3 支付方式3

（1）当T≤M时，零售商的利息支出与利息收益与支付方式1相同，因此略。

（2）当T≥M时，且cQ－sDM－sIeDM2／2≤0时，零售商的利息支出与利息收益与支付方式2相同，因此略。

（3）当T≥M时，且cQ－sDM－sIeDM2／2＞0时，零售商将选择在M点支付部分货款，同时零售商根据未付的剩余货款额及销售收入和利息支出情况，可以确定能够支付完所有货款的时刻K，那么K时刻之后零售商销售所得收入都将为纯利润，同时还有新的利息收入，不需要支付利息，如图7所示，图7中实线部分表示利息支出变化情况，虚线部分表示利息收益变化情况。即由＝sD（K－M），得K＝（2cQ－sIeDM2）／2sD。

因此，零售商的总成本函数可总结为：

3 模型的求解与分析

（1）对（5）式进行一阶、二阶求导，可得：

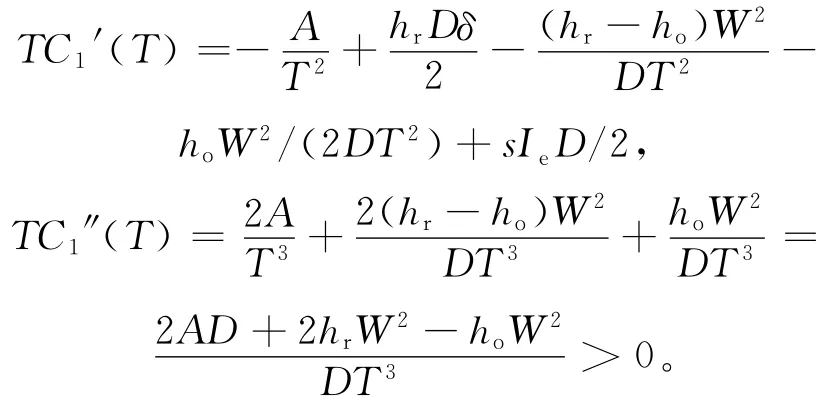
因为TC1″（T）＞0，即TC1（T）是关于T的凸函数，所以TC1（T）在（0，M）内存在唯一最小值点。令TC1′（T）＝0，求得：

同时为保证T1≤M，可得：Δ1＝M2（hrD2δ＋sIeD2）－2AD－（2hr－ho）W2≥0，即当Δ1≥0时，T1是零售商的最小订货周期。

（2）对（6）式进行一阶、二阶求导，可得：

因为TC2″（T）＞0，即TC2（T）是关于T的凸函数，所以TC2（T）在（M，＋∞）内存在唯一最小值。令TC2′（T）＝0，求得：

同时由T2≥M，可得：

即当Δ1＜0≤Δ2时，T2是零售商的最小订货周期。

（3）对（7）式进行一阶、二阶求导，可得：

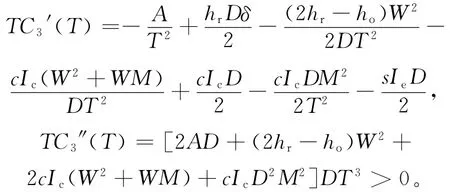
因为TC3″（T）＞0，即TC3（T）是关于T的凸函数，所以TC3（T）在（t2，＋∞）内存在唯一最小值。

令TC3′（T）＝0，求得：

同时由于（T3－M）－Δ2＝2cIc［W2＋WM］＞0，即当Δ2＜0时，T3是零售商的最小订货周期。

（4）对（8）式进行一阶、二阶求导，可得：

因为TC4″（T）＞0，即TC4（T）是关于T的凸函数，所以TC4（T）在 （M，sM／c＋sIeM2／2c） 内存在唯一最小值。令TC4′（T）＝0，求得：

同时由T4≤sM／c＋sIeM2／（2c），可得：

即当Δ1＜0≤Δ3时，T4是零售商的最小订货周期。

（5）对（9）式进行一阶、二阶求导，可得：

因为TC5″（T）＞0，即TC5（T）是关于T的凸函数，所以TC5（T）在 （sM／c＋sIeM2／2c，＋∞）内存在唯一最小值。令TC5′（T）＝0，求得：

其中，X＝2AD＋（2hr－ho）W2＋sIcIeD2M3＋2s（Ic－Ie）D2M2；Y＝hrD2δ＋2cIcD2－sIeD2。

同时 由T5≥ （sM／c＋sIeM2／2c），可 知 当Δ3＜0时，T5是零售商的最小订货周期。

（6）对（10）式进行一阶、二阶求导，可得：

因为TC6″（T）＞0，即TC6（T）是关于T的凸函数，所以TC6（T）（在（2cT－sIeM2）／2s，＋∞）内存在唯一最小值。令TC6′（T）＝0，求得：

即当Δ3＜0且Δ4≥0时，T6是零售商的最小订货周期。

4 分析结论

（1）在支付方式1下，当Δ1≥0时，最小周期T＊＝T1，零售商的最小成本为TC1（T1）；当Δ1＜0≤Δ2时，最小周期T＊＝T2，零售商的最小成本为TC2（T2）；当Δ2＜0时，最小周期T＊＝T3，零售商的最小成本为TC3（T3）。

（2）在支付方式2下，当Δ1≥0时，最小周期T＊＝T1，零售商的最小成本为TC1（T1）；当Δ1＜0≤Δ3时，最小周期T＊＝T4，零售商的最小成本为TC4（T4）；当Δ3＜0时，最小周期T＊＝T5，零售商的最小成本为TC5（T5）。

（3）在支付方式3下，当Δ1≥0时，最小周期T＊＝T1，零售商的最小成本为TC1（T1）；当Δ1＜0≤Δ3时，最小周期T＊＝T4，零售商的最小成本为TC4（T4）；当Δ3＜0且Δ4≥0时，最小周期T＊＝T6，零售商的最小成本为TC6（T6）。

5 算 例

设某零售商订购某商品，根据历史销售数据知该物品的采购价格为c＝10，市场销售价格为s＝15，物品的补货率P＝6 000，OW 中ho＝0.7，RW 中hr＝1，Ic＝0.08，Ie＝0.03，若供应商给予零售商的购买费用延期支付期M＝0.5。

根据W、A和D的变化情况，可得表1所列的数据，分别来判定最优支付方式、最优周期和最优订货量，以及最小成本。

由表1可知，随着需求量D的不断增加，零售商的订货周期不断在下降，订货库存量不断地增加，同时降低了零售商的总成本，增加了利润收益。从3种不同的支付方式可以看出，支付方式1的订货周期较长，但订货成本较小，库存较大；支付方式2和支付方式3在需求量较低时差别比较明显，需求量大时，由于周期比较短，所以差别不明显。总之，3种支付方式各有优势，不同的需求和库存量情况下，它们的最优值是不同的。为了使得整个订货周期内的库存变化达到最优，零售商先通过判定条件来选择最优支付方式，再计算最佳周期和成本量是很有效的方法。

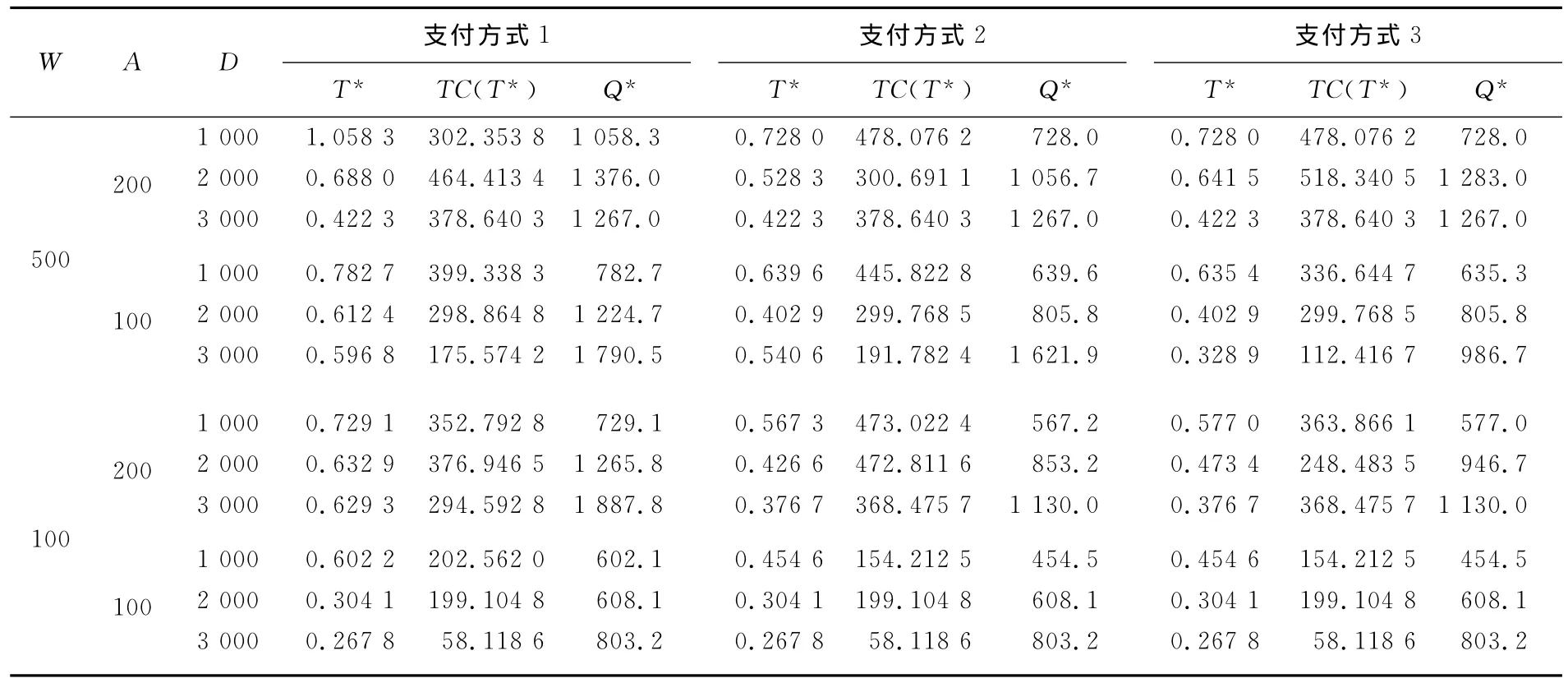
表1 W、A和D的变化对最优订货与最优支付策略的影响

6 结束语

在供应商给予零售商延期支付的条件下，如果零售商仅仅考虑支付货款的某一种方式，不一定就能达到最优订货量和最小订货周期，因为在不同的变量和因素的影响下，零售商的最优订货和付款策略是不一样的，因此，零售商为了使自己的成本最小化，收益最大化，可根据本文所给出的判断条件来确定一种最佳支付方式，确定最小订货周期和最小成本，得到最优订货策略，这对零售商具有很大的意义。

［1］Hartely V R.Operations research：a managerial emphasis［M］.Santa Monica，CA：Good Year，1976：315－317.

［2］Sarma K V S.A deterministic order－level inventory model for deteriorating items with two storage facilities［J］.European Journal of Operational Research，1987，29：70－72.

［3］Pakkala T P M，Achary K K.A deterministic inventory model for deteriorating items with two warehouses and finite replenishment rate［J］.European Journal of Operational Research，1992，57：71－76.

［4］杨爱峰，李佐平.基于产品变质和零售商部分延期支付的EOQ模型［J］.合肥工业大学学报：自然科学版，2011，34（9）：1413－1418.

［5］杨志林，周永务，杨善林.带有两货栈具有抛物型需求的变质性物品经济批量问题［J］.系统工程理论方法应用，2005，14（4）：376－378.

［6］杨善林，周永务.两货栈库存模型：考虑时变需求和价格折扣［J］.系统工程学报，2003，18（6）：498－505.

［7］Yang H L.Two－warehouse partial backlogging inventory models for deteriorating items under inflation［J］.Int J Production Economics，2006，103：362－37.

［8］Das B，Maity K，Maiti M.A two－warehouse supply－chain model under possibility／necessity／credibility measures［J］.Mathematical and Computer Modeling， 2007， 46：398－409.

［9］Liang Yanlai，Zhou Fangming.A two－warehouse inventory model for deteriorating items under conditionally permissible delay in payment［J］.Applied Mathematical Modeling，2011，35：2221－2231.

［10］Chang Chuntao，Wu S J，Chen L C.Optimal payment time with deteriorating items under inflation and permissible delay in payments［J］.International Journal of Systems Science，2009，40（10）：985－993.

［11］Chung K J，Huang T S.The optimal retailer’s ordering policies for deteriorating items with limited storage capacity under trade credit financing［J］.Int J Production Economics，2007，106：127－145.

［12］Jamal A M M，Sarker B R，Wang Shaojun.Optimal payment time for a retailer under permitted delay of payment by the wholesaler［J］.Int J Production Economics，2000，66：59－66.

［13］Liao J J，Huang Kuonan.Deterministic inventory model for deteriorating items with trade credit financing and capacity constraints［J］.Computers ＆Industrial Engineering，2010，59：611－618.

［14］Cheng Meichuan，Lou Kuoren，Ouyang L Y，et al.The optimal ordering policy with trade credit under two different payment methods ［J］.Mathematics Subject Classification，2010，18：413－428.

Retailer’s optimal ordering and payment strategy under two－warehouse and permissible delay of payment

YANG Ai－feng1，2， YANG Xiao－qin1，2， HU Xiao－jian1，2
（1.School of Management，Hefei University of Technology，Hefei 230009，China；2.Key Laboratory of Process Optimization and Intelligent Decision Making of Ministry of Education，Hefei University of Technology，Hefei 230009，China）

It is assumed that the supplier offers the retailer a delay payment period and the retailer can select one of three kinds of payment methods.After calculating some critical indices of the interest income and interest expenses under different payment methods，the two－warehouse inventory model is established.By analyzing and solving the model，the minimal cycle time and cost are obtained.So the retailer can determine which kind of payment way to adopt，and the corresponding optimal ordering strategy as well.Finally，a numerical example is conducted to verify the model，and the results accord with the actual situation.

delay in payment；two－warehouse；payment method；inventory；optimal ordering

F252

A

1003－5060（2013）02－0236－07

10.3969／j.issn.1003－5060.2013.02.023

2012－07－16；

2012－10－29

国家自然科学基金资助项目（70971035）；安徽省软科学计划资助项目（12020503075）

杨爱峰（1976－），女，河南濮阳人，博士，合肥工业大学副教授，硕士生导师；

胡小建（1965－），男，安徽安庆人，博士，合肥工业大学教授，硕士生导师.

（责任编辑 张 镅）