求解介质中磁化电流的方法探究

路俊哲

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

求解介质中磁化电流的方法探究

路俊哲

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

本文针对具有对称性较高、磁化电流分布比较容易确定的问题，总结和讨论一种计算磁化电流的方法；借助此方法求解几类典型的、载有恒定电流的磁场中磁化电流；总结出此方法的解题步骤，探究让学生更少的使用和记忆物理公式而更多地考虑和理解物理本质的一种解决问题的思路.

磁化电流；安培环路定理；磁感应强度；磁场强度

在电磁理论中，研究介质的磁化是非常重要的，也有很多学者对介质磁化电流进行了深入的研究[1-4].所谓磁化电流只是一种等效电流，是大量分子磁效应的一种表示，磁化电流的分布反映着介质整体的磁化状态，因此，磁介质的磁化电流与磁化强度密切有关.一般来说，磁介质内任一曲面S的磁化电流[5-9]IM为：

上式表示磁介质中任一曲面S的磁化电流I等于磁化→强度M沿这曲面的边线L的积分，即磁化强度的环流.由此可知，要计算介质在外磁场作用下所产生的磁化电流的大小，可直接按照磁化电流的定义求得.而要由定义式解磁化电流必须先求出磁化强度，因为磁化强度M→是描述介质磁化程度的物理量，其定义为单位体积内分子磁矩的矢量和，是由各分子磁矩的大小和排列情况的统计平均结果所决定，故磁化强度与介质的磁感强度有关，对于线性非铁磁性物质，磁化强度→M与磁感强度B→成正比：

其中比例系数χm称为磁化率.于是通过（2）式求得磁化强度M→代入磁化电流的定义式即可求得磁化电流.这就是求解磁化电流的第一种方法.本文将介绍另外一种求解介质中磁化电流的方法，并利用这两种方法分别求解几类典型的、载有恒定电流导线的磁场中磁化电流，通过求解进行对比研究和总结.

1 另一种求解磁化电流的方法

这种方法在原理上与文献[10]中求解关于导体中电介质和导体问题的计算方法类似，它是由介质中磁场的安培环路定理直接求解的.存在介质后，传导电流和磁化电流都要产生磁场，闭合的传导电流和磁化电流都与闭合的磁感线相互交链，磁场的环流由被闭合路径所圈围的传导电流与磁化电流共同决定.但当引入一个新的物理量磁场强度→H→后，H的环流只与传导电流有关.即

此为有介质时磁场的安培环路定理，I0表示闭合曲线所包围的所有传导电流的代数和.在某些有对称性的场合，可以方便地根据传导电流的分布求出磁场强度→H，进而求得磁感应强度.对于各向同性的线性磁介质，→H与的关系可以进一步简化.令，此时的→H是考虑了磁介质影响以后的磁场强度.但另一方面，因为传导电流和磁化电流都产生磁场，我们可以将磁化电流视为传导电流，直接运用真空中磁场的安培环路，即

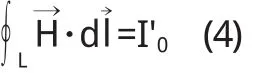
其中I'0=I0+IM为等效传导电流，由于磁介质的影响在（4）式右边的磁化电流已有体现，因此此时的，是真空中的磁场强度.

2 磁化电流的求解方法的应用

2.1 无限长载流直导线在介质中产生的磁化电流

2.1.1 一般文献的求解方法

如图1，选取一个包围传导电流的圆作为环绕路径，应用介质中的安培环路定理（3）式得：H=，由（2）式得运用磁化电流的定义（1）式得：

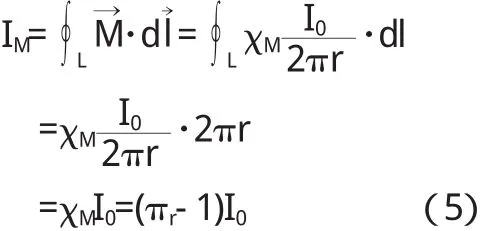
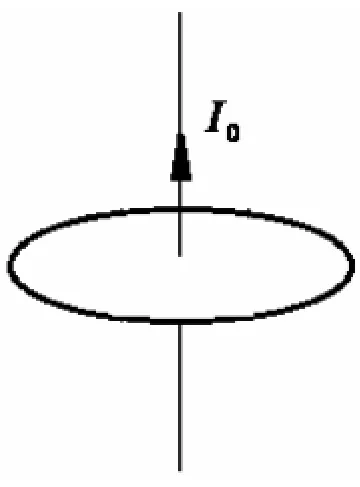
图1

2.1.2 本文的求解方法

应用介质中的安培环路定理（3）式得：

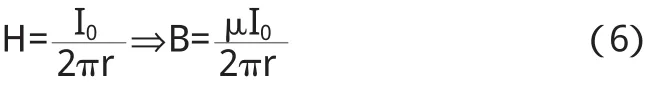
将磁化电流视为传导电流，直接运用真空中安培环路定理（4）式得：

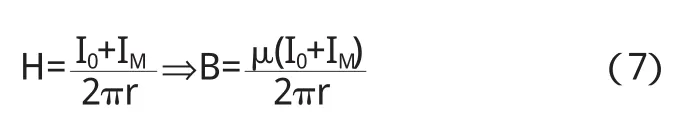
由(6)、(7)式得：

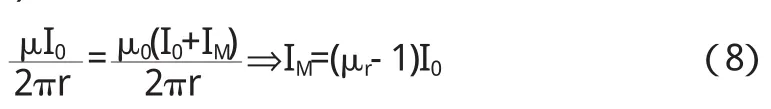
与（5）式结果相同.

2 无限长载流螺线管在介质中产生的磁化电流

2.1 一般文献的求解方法

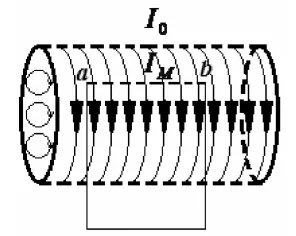
图2

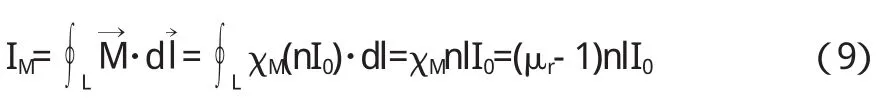
2.2 本文的求解方法

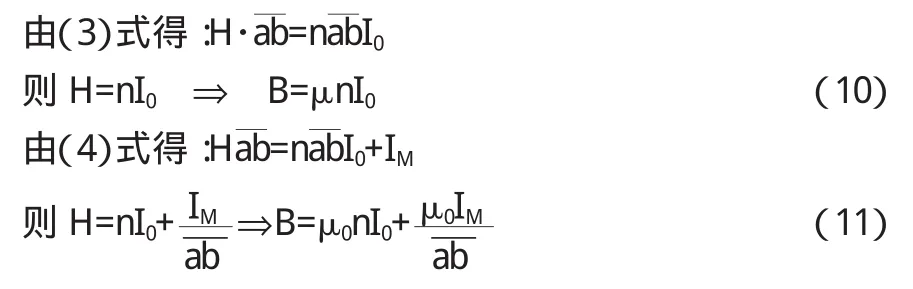
由(10)、(11)得：

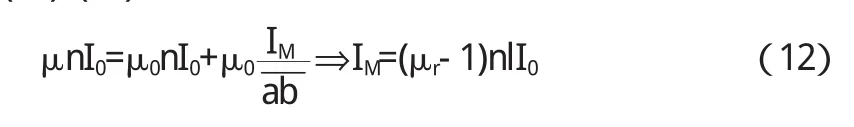
与（9）式结果相同.

3 均匀载流无限大平面在介质中产生的磁化电流

3.1 一般文献的求解方法

图3

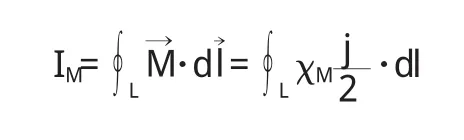
3.2 本文的求解方法

与（13）式结果相同.

通过以上三个例子总结本文求解介质中磁化电流方法步骤为：第一步：利用介质中的安培环路定理，求出磁感应强度.第二步：将磁化电流等效于传导电流，利用真空中的安培环路定理，得到.第三步：将以上两步的联立求解即可求得磁化电流IM.

4 结语

本文首先给出一种不同于一般文献求解介质磁化电流的方法，然后运用两种方法分别求解无限长载流直导线在介质中产生的磁化电流、无限长载流螺线管产生的磁化电流、均匀载流无限大平面产生的磁化电流的求解，结果都是相同的；最后总结本文所给求解磁化电流方法的解题步骤.通过本文，进一步明确运用安培环路定理求解问题的重要性.这种方法的优点是可以不用公式计算磁化电流，因此无需求解磁化强度，也无需找出介质的磁化率，所以说采用本文总结和讨论的方法可以更少地使用公式，只需要学习一个公式来解决所有关于磁场中的介质问题.少一些数学表达，而多一些物理分析，从这个角度上看，总结和讨论这种方法对学生更深层次的把握物理本质是有益的.

这种方法的缺点是仅适用于具有对称性较高、磁化电流分布比较容易确定的问题，如果对称性不高，只能应用公式求磁化电流，而求解磁化强度涉及到的数学知识很多，难度也较大.但是，普通物理阶段绝大部分问题都是具有比较高的对称性的.因此，另辟蹊径，多一种方法，多一种选择，对发散学生的思维也是有益的.

〔1〕何立善.关于介质磁化电流的一个问题[J].佛山师专学报（自然科学版），1986，5(4)：87-88.

〔2〕吴庭竺.关于磁介质内部的磁化电流[J].大学物理,1992,11 (1)：27-28.

〔3〕康文秀，陈艳梅.介质磁化电流的简化处理[J].河北大学学报（自然科学版），1996,16(1)：81-84.

〔4〕罗惠霞，李应乐.介质磁化的进一步讨论[J].玉林师范高等专科学校学报，2000，21(3):45-46.

〔5〕梁灿彬，秦光戎，梁竹健.电磁学[M].北京:高等教育出版社，2006.283-291.

〔6〕郭硕鸿.电动力学[M].北京:高等教育出版社，2008.18-24.

〔7〕程守洙，江之永.普通物理学[M].北京:高等教育出版社，2003.280-289.

〔8〕贾瑞皋，薛庆忠.电磁学[M].北京:高等教育出版社，2003.210-223.

〔9〕马文蔚，周雨青，解希顺.物理学教程[M].北京:高等教育出版社，2006.108-111.

〔10〕路俊哲,张冬波，等.关于导体中电介质和导体问题的一种计算方法[J].新疆师范大学学报(自然科学版)，2013（1）：48-49.

O441.2

A

1673-260X（2013）09-0010-02

新疆师范大学优秀青年教师科研启动基金项目（XJNU1215）；新疆师范大学理论物理自治区重点学科招标课题（13XSQZ0601）