分圆域Q(ζ24)的幂元整基
2013-07-14李乃微
李乃微
(辽宁大学数学院,辽宁沈阳110136)
分圆域Q(ζ24)的幂元整基
李乃微
(辽宁大学数学院,辽宁沈阳110136)
伽罗瓦数域L称有一个幂元整基,如果其代数整数环具有形式Z(α),其中α∈L.此时称α是L的幂元整基生成元.设α,β是L的两个幂元整基生成元,若β=m±σ(α),m∈Z,σ∈Gal(L/Q),则称α与β等价.本文主要研究分圆域Q(ζ24)的幂元整基问题.分圆域Q(ζ24)的代数整环是Z[ζ24],所以ζ24是Q(ζ24)的幂元整基生成元.设α是Q(ζ24)的幂元整基生成元,证明了当α+∉Z时,Z[α]=Z[ζ24],则α与ζ24等价.从而给出在此条件下分圆域Q(ζ24)的所有幂元整基生成元.
分圆域;幂元整基;生成元;单位
1 基础知识
先给出本文中涉及到的基础知识,包括一些定义和定理.并且假设数域扩张均为伽罗瓦扩张.
定义1.1设L/K为数域扩张,[L:K]=n.σi:L→C(1≤i≤n)是L的n个K-嵌入.对于α∈L定义称作是元素α∈L对于扩张L/K的范.
引理1.2设α,β∈L,L,K是两个数域,[L:K]=n,σi∈Gal (L/K),则NL/K(αβ)=NL/K(α)NL/K(β)和NL/K(αn)=(NL/K(α))n
定义1.3设L/K是数域的n次扩张,σ1,…,σn是L到C的n个K嵌入.α1,…,αn为L中任意n个元素.定义dL/K(α1,(||表示方阵的行列式),称作是元素对于扩张L/K的判别式.
引理1.4设L=K(α),[L:K]=n,f(x)是α在K上的极小多项式,α1=α,α2,…,αn为f(x)的n个复根,则dL/K(1,α,…,αn-1)=
定理1.5(1)[Q(ζn):Q]=φ(n),并且ζn=e2m/n在Q上的极小多项式为叫作分圆多项式),φ(n) =deg(øn(x)).
(2)Q(ζn)/Q为伽罗瓦扩张,并且Gal(Q(ζn)/Q)≅(Z/nZ)*即对任意σk∈Gal(Q(ζn)/Q),使得
引理1.6假设K是一个数域,Ok是K的整数环,设α1, α2,…,αn∈Ok,如果
(1)dK(α1,α2,…,αn)=d(K),或者
(2)dK(α1,α2,…,αn)是无平方因子的非零有理整数,则α1, α2,…,αn是域的一组整基.
(1)OK=Z[ζm],从而是域K的一组整基;

引理1.8设K为n次数域,σ1,…σn是K到C中的n个嵌入,u∈OK,则
(a)u∈UK⇔NK/Q(u)=±1;
(b)u∈WK⇔|σi(u)|=1(1≤i≤n).
2 主要证明
本文主要研究的是分圆域Q(ζ24)的幂元整基问题,我们知道Z[ζ24]是Q(ζ24)的整数环.下面证明:当α+∉Z时,Z[α]=Z [ζ24],当且仅当α与ζ24等价.下面用ζ表示ζ24.
记Gak(Q(ζ)/Q)={σ1,σ5,σ7,σ11,σ13,σ17,σ19,σ23,}其中σi(ζ)=ζi.
Gal(Q(ζ)/Q)=〈σ-1〉×〈σ5〉×〈σ7〉.从L.Washington我们进行一些简单的研究.
取α∈Z[ζ],满足Z[α]=Z[ζ]当且仅当d[α]=d[ζ],d[α],d[ζ]分别是α,ζ的判别式.这等价于

其中f(x)为α在Q上的极小多项式,g(x)=x8-x4+1为ζ在Q上的极小多项式.
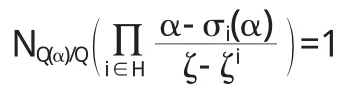
引理2.1设α∈Z[ζ],H={1,5,7,11,13,17,19,23},则下面几个结论等价:
(i)Z[α]=Z[ζ];
(ii)NQ(α)/Q(α-σi(α))=±NQ(ζ)/Q(ζ-ζi),i∈H;

则我们可以得到
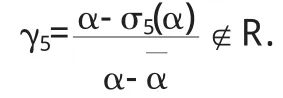
设τ5=1-γ5,π1=1-ζ6,由引理2.1知γ5和均为单位.因为γ5和是单位,所以存在r,s∈Z,使得

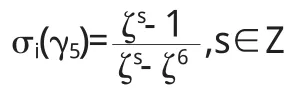
综上,我们证明了引理2.2.
引理2.3假设σ5∈Gal(Q(ζ)/ζ)和α∈Z[ζ].如果Z[α]=Z [ζ],并且
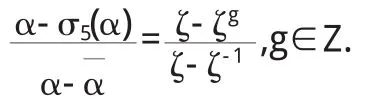
则α=n±ζ,n∈Z.
证明假定Z[α]=Z[ζ]并且等式

成立.我们首先证明g只能等于5.
设π1=1-ζ6,将等式两边都模π1,因为1(modπ1),所以我们有1(modπ1).从而6| (g-5),也就是说g∈{5,7,13,19}
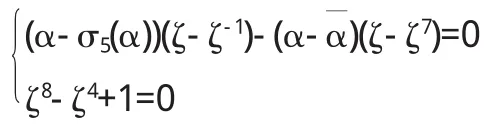
方程组无解.故g≠7.
同理,我们可以得到g≠13和g≠19.


联立等式(3)和(4)整理可得
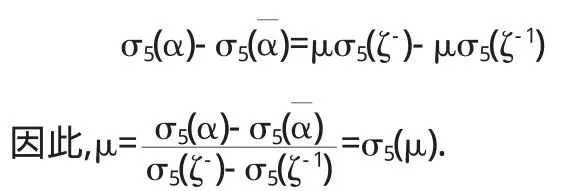
并且μ由σ5所确定.因为σ5是Gal(Q(ζ)/ζ)的生成元,也就是说μ由整个伽罗瓦群所确定并且μ∈Q.由引理2.1可知μ为单位,则可得μ=±1.
因为σ5(μ)=μ,所以(3)等价为σ5(α-μζ)=α-μζ.因此α-μζ也被Gal(Q(ζ)/ζ)所确定,并且α-μζ∈Z.因为μ=±1,我们可以得到α=n±ζ,n∈Z.
综上,证明了引理2.3.

则我们可以得到
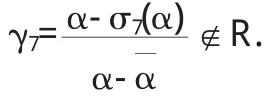
设τ7=1-γ7,π2=1-ζ8,由引理2.1知γ7和均为单位.所以存在m,n∈Z,使得γ7=ζmγ7,τ7=ζnτ7.由于解得
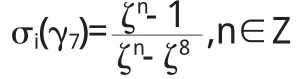
综上,我们证明了引理2.4.
引理2.5假设σ7∈Gal(Q(ζ)/ζ)和α∈Z[ζ].如果Z[α]=Z [ζ],并且

则α=n±ζ,n∈Z.
证明假定Z[α]=Z[ζ]并且等式

成立.我们首先证明h只能等于7.
设π2=1-ζ8,将等式两边都模π2,因为1(modπ2),所以我们有1(modπ2).从而8| (h-7),也就是说h∈{7,9,17}.

方程组无解.故h≠9.
同理,我们可以得到h≠17.


联立等式(6)和(7)整理可得

并且v由σ7所确定.因为σ7是Gal(Q(ζ)/ζ)的生成元,也就是说v由整个伽罗瓦群所确定并且v∈Q.由引理2.1可知v为单位,则可得v=±1.
因为σ7(v)=v,所以(6)等价为σ7(α-vζ)=α-vζ.因此α-vζ也被Gal(Q(ζ)/ζ)所确定,并且α-vζ∈Z.因为v=±1,我们可以得到α=n±ζ,n∈Z.
综上,证明了引理2.5.
由上面的引理,我们将证明本文主要的结论.

(1)由已知可知Z[α]=Z[ζ24],设并且可由引理2.2可知使得
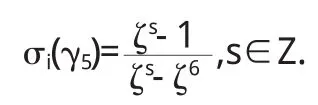
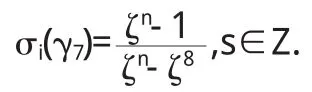
设σ-1(α)=α^,所以
则由引理2.5可得α^=n±ζ24,n∈Z.所以α与ζ24等价.
充分性.若α与ζ24等价,显然有Z[α]=Z[ζ24].
〔1〕Bremner A.On power bases in cyclotom ic number fields [J].Number theory,1988,28(3):288-298.
〔2〕Robertson L.Power bases for cyclotom ic integer rings[J]. Number Theory,1998,69(1):98-118.
〔3〕W ashington L J.Introduction to cyclotom ic fields(2nd) [M].New York:Springer Verlag,1997.
〔4〕冯克勤.代数数论[M].上海:科学出版社,2001.
〔5〕Xia jianguo,Wang shaozu.Power bases for the cyclotomic field[J].Sichuan Normal University(Natural Science), 2005,28(6),664-666.
O156.2
A
1673-260X(2013)09-0005-03
