一类特殊双色有向图的指数界

罗美金

(河池学院数学系，广西宜州 546300)

0 引言

设D是一个有向图，D的一条长为l的途径是指连续的顶点序列v1，v2，…，vl+1，其中对所有的i=1，2，…，l，D 中有从 vi到 vi+1的弧．如果 v1，v2，…，vl+1互不相同，则称该途径是一条长为 l的路．如果 v1=vl+1，则称为一条闭路或圈．如果D是包含红弧和蓝弧的有向图，则称D是一个双色有向图．双色有向图D是强连通的，如果D中每一对顶点(i，j)都存在从i到j的途径．给定D中的一条途径ω，用r(ω)和b(ω)－分别表示ω中红弧和蓝弧的条数，称 ω 为一条(r(ω)，b(ω))途径，ω 的分解为向量(r(ω)，b(ω))或(r(ω)，b(ω))T．

一个双色有向图D是本原的，当且仅当存在非负整数h和k，且h+k＞0，使得D中的每一对顶点(i，j)都存在从i到j的(h，k)－途径，h+k的最小值定义为双色有向图D的本原指数，记为exp(D)．

设C={γ1，γ2，…，γl}是D的圈的集合，定义D的圈矩阵M是一个2×l矩阵，它的第i列是γi的分解．M的content(记为content(M))定义为0如果M的秩小于2，否则定义为M的所有非零2阶主子式的最大公因数．

引理1［1］一个至少包含一条红弧和一条蓝弧的双色有向图D是本原的，当且仅当D是强连通的，且content(M)=1．

双色有向图和非负矩阵对之间存在一一对应关系，近几年对本原双色有向图本原指数的研究已经取得了一些重要成果，见文献［1－6］．本文研究了一类特殊的双色有向图D，它的未着色有向图如图1所示．

图1 D的未着色有向图

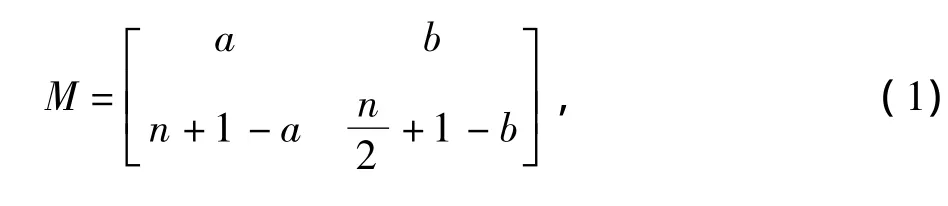
其中a，b为正整数．

1 本原条件

以下分两种类型讨论双色有向图D的本原指数:

2 指数界

定理2 设双色有向图D是本原的，且属于类型1，则

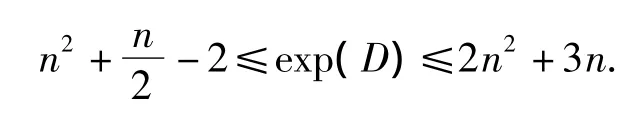
设存在一对非负整数(h，k)，使对D中所有顶点对(i，j)，都有一条从i到j的(h，k)－途径．取i=j=n+1，则存在非负整数u和v，有

有非负整数解，即

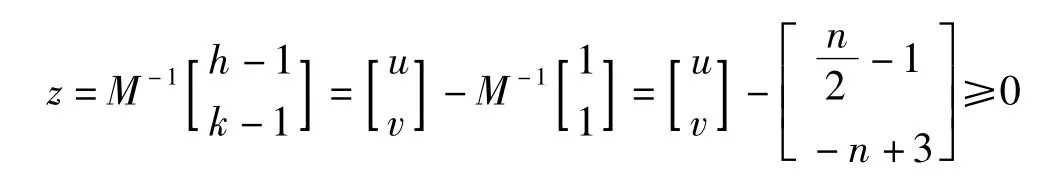
或

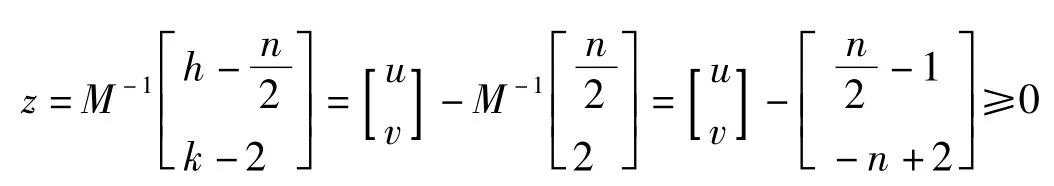
有非负整数解，即

所以 v≥n－2．

再证exp(D)≤2n2+3n．

只需证明D的任意一对顶点(i，j)，都有一条(n2－n，4n)－途径．对D中的任意一对顶点(i，j)，记pij是从 i到 j的最短路，r(pij)=s，b(pij)=t．可得，

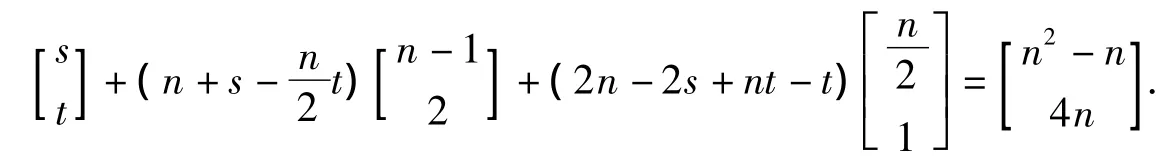
考虑以下两种情况:

情况2:pij包含)－圈上的顶点．此时，0≤s≤n－1，0≤t≤2．

a)若 t=0，则0≤s≤n－1;b)若 t=1，则 0≤s≤n－1;c)若 t=2，则0≤s≤n－2．

综上所述，exp(D)≤2n2+3n．定理得证．

类似定理2的证明，可得定理3．

定理3 设双色有向图D是本原的，且属于类型2，则

3 极图刻划

考虑以下两种情况:

情况2:pij包含－圈上的顶点．此时，0≤s+t≤n－1．

结合定理 2、3、4，同理，类似可证得定理 5、6、7．

定理5 设双色有向图D是本原的，且属于类型2，则exp(D)=2n2+3n，当且仅当弧或弧n+1→1→2是蓝色的，其它弧是红色的．

［1］Shader B L，Suwilo S．Exponents of nonnegative matrix pairs［J］．Linear Algebra Appl．，2003，363:275－293．

［2］SHAO Yanling，GAO Yubin，SUN Liang．Exponent of a class of two－colored digraphs［J］．Linear and Multilinear Algrbra，2005，53(3):175－188．

［3］罗美金，高玉斌．一类恰含三个圈的三色有向图的本原指数［J］．山东大学学报(理学版)，2008，43(1):65－72．

［4］罗美金，高玉斌．一类双色有向图的本原指数［J］．中北大学学报(自然科学版)，2008，29(2):95－100．

［5］GAO Yubin，SHAO Yanling．Exponent of two－colored double directed cycles［J］．Journal of Natural Science of Heilongjiang University，2004(4):55－58．

［6］白竹香，邵燕灵．一类双色有向图的指数［J］．中北大学学报(自然科学版)，2007，28(2):100－103．