一类复蒙日－安培方程Dirichlet问题数值解探讨(二)

殷慰萍

(首都师范大学数学科学学院，北京 100048)

0 引 言

本文是数值解探讨(二)，引言与(一)相同，为方便读者依然保留，看过(一)的读者可以直接跳过引言．数值解法属于计算机科学范畴的一个研究方向，本文用多复分析的方法来进行研究，因而本文是计算机科学和数学科学的交叉，或者说是数值计算与多复分析的交叉．

由于在一些领域，如:微分几何、变分法、最优化问题及传输问题等中的重要作用，近年来，经典的蒙日－安培方程及蒙日－安培型方程成为一个新的研究热点．丘成桐认为复蒙日－安培算子，是微分几何中5个重要的微分算子之一．他的最有影响且最重要的工作，例如，卡拉比猜测的证明以及负定第一陈类的紧Kaehler流形上Kaehler－Einstein度量的存在性，都各自等价于一类复蒙日－安培(Monge－Amp è re)方程的可解性．因此研究蒙日－安培方程是相当重要的．莫毅明，丘成桐和郑绍远在上世纪80年代初期证明了在高维的复数空间Cn中的任何有界的拟凸域D存在唯一的完备Kaehler－Einstein度量［1，2］．事实上他们证明了如下复蒙日－安培方程Dirichlet问题的多重强次调和函数解g的存在和唯一性．

此处的多重强次调和函数解g生成了域D如下的完备Kaehler－Einstein度量:

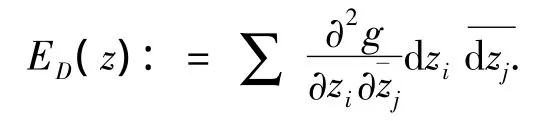
多重次调和函数g称为多重强次调和函数是g要满足如下条件:

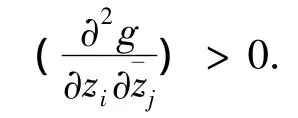
由于蒙日－安培方程是完全非线性的，其求解一直是一个困难的问题．上面提到的丘成桐等人的工作也是仅仅证明了相应问题的解的存在性．他们从未给出解的表达式来，这比之于存在性的证明更为困难，因为从事微分方程研究工作的都知道解的具体表达式在绝大多数的情况下根本是求不出来的．因此对于具体的复蒙日－安培方程Dirichlet问题的求解，只能寄希望于数值解法．作者请教了很多专家，他们认为这问题很重要也很难，目前还没有一个成熟的对复蒙日－安培方程的数值解法．

本文试图对第二类Carten－Hartogs域上的复蒙日－安培方程的Dirichlet问题的数值解法作一个探讨．作者不是探讨该方程的数值方法的本身，而是把这个复蒙日－安培方程的Dirichlet问题转化为一个非线性二阶常微分方程的二点边值问题，而后者的数值解法是有较为成熟的研究．这对纯粹数学家而言，已经达到了所谓数值解法探讨的目的，而且在具体计算上也大大降低了计算的复杂性．同时在一些特殊的情况下，得到了该方程的Dirichlet问题解的分析表达式，它可以作为检验该问题的数值解法的一个标准样本．

第二类Cartan－Hargogs域的定义为:

其中RⅡ(p)是华罗庚研究过的第二类典型域，即

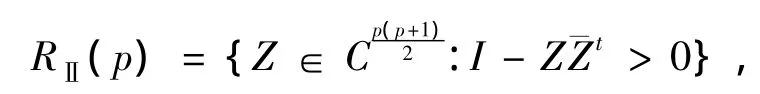
这里的Z是p阶的对称复矩阵，Z＞0表示矩阵Z是正定矩阵．珔Z，Zt分别表示矩阵Z的共轭和转置．从YⅡ的Bergman核函数的显表达式可知该核函数是Bergman穷竭的，因而YⅡ是一个有界拟凸域，所以下述问题(1)有解且惟一．本文探讨如下的复蒙日－安培方程的Dirichlet问题的数值解:

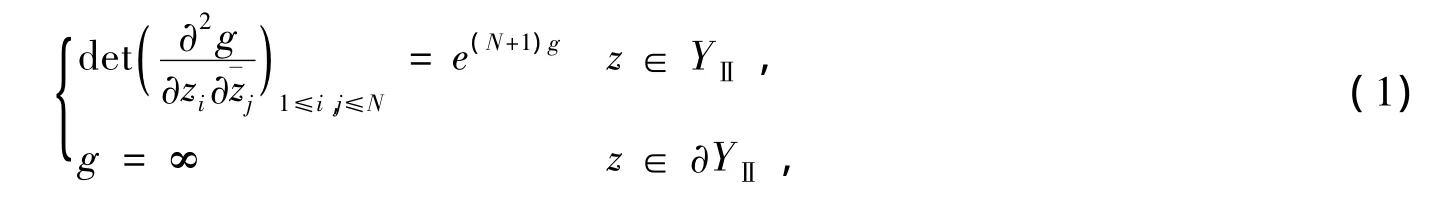
Z1是把

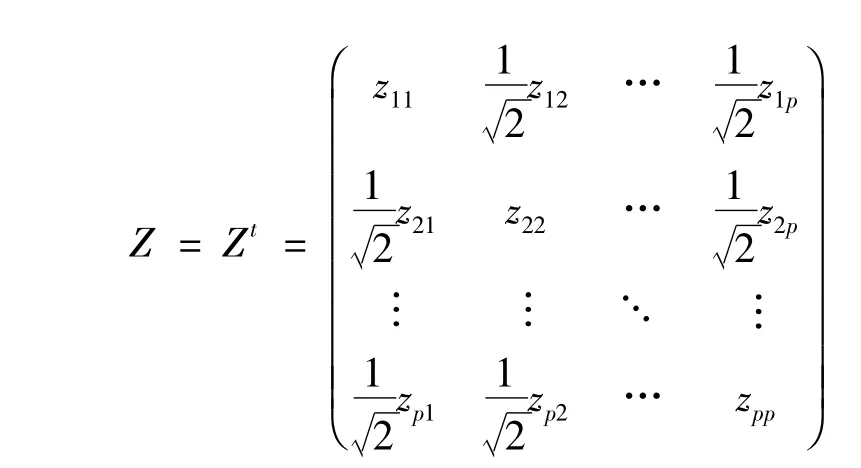
中的元素zij按其上三角的元素次序排成一个具有个元素的向量，即

Z2是把 W 的元素排为(w1，w2，…，wN2)令

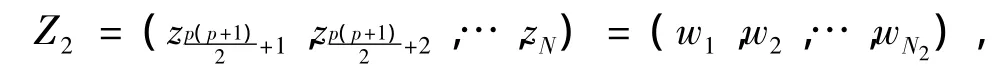
这样，YⅡ中的点(Z，W)可以表示成具有N个元素的向量z=(Z1，Z2)．

本文首先把上述Dirichlet问题化为二阶常微分方程的二点边值问题，这样就把问题(1)的数值解转化为二阶常微分方程的二点边值问题的数值解，而后者是有较为成熟的研究的(参见［3］);其次，在一些特殊的情况下，得到了问题(1)的解的分析表达式．

1 准备知识

(1)以下变换是YⅡ(N2，p，K)的全纯自同构，这些变换的集合记之为Aut(YⅡ):

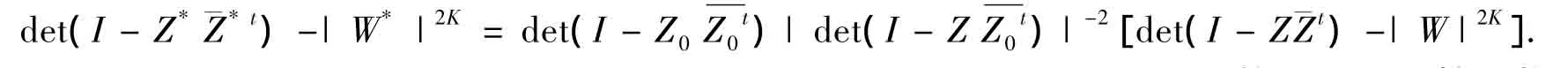
这证明了上述变换是YⅡ(N2，p;K)的全纯自同构．也可参阅［4］．由［4］可知，YⅡ的Bergman核函数已经求出，而且当点从内部趋向于边界时，该核函数趋向于无穷，因而YⅡ是有界拟凸域．即总是(1)有解且惟一．

证．这可以直接计算而得，也可参阅［4］．因而任何以X为变量的函数F(X)都是在Aut(YⅡ)下不变．

就是域YⅡ的Kaehler－Einstein度量，由于该度量是不变度量，根据不变性，在(2)中的变换(Z*，W*)=F(Z，W)=F(z)下，就有

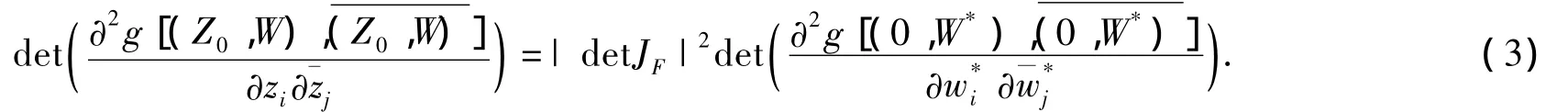
其中w*是z在F(z)下的像，也是复N维向量，即表示变换F的Jacobian矩阵，即

故

根据典型域熟知的理论［3］，我们有

这样，当Z=Z0时，(3)式就变成

这就是问题(1)中第一式的左端的表示式，它可以通过YⅡ的全纯自同构(2)而化为(4)式右端的形式．因此要计算(1)式的左端实质上只要计算

若g是问题(1)的解，则(4)式右端应当等于e(N+1)g，即

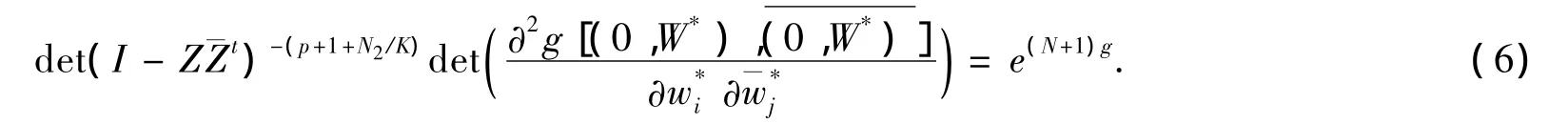
因此若取

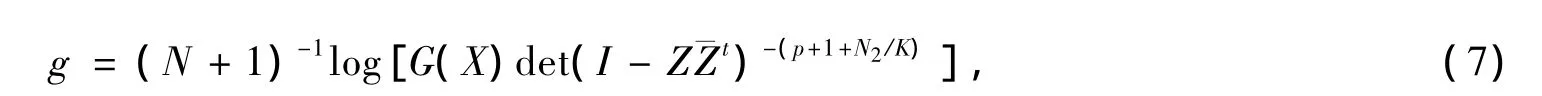
则(6)式就等价于

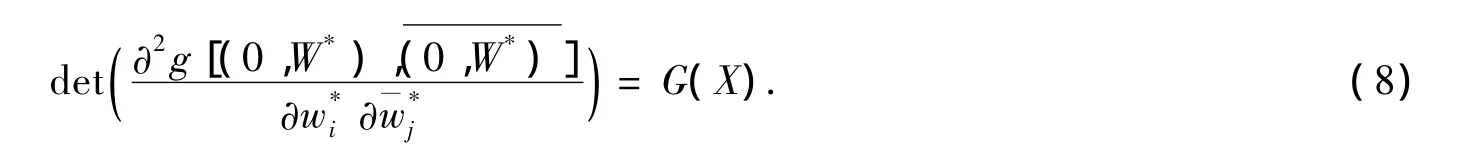
由此可见，若(8)式左端能用X、G(X)及其导数表示，则(1)式中的蒙日－安培方程就等价于一个常微分方程了．答案是肯定的，详见下节．

2 化蒙日－安培方程为常微分方程

为了方便计算，现在把(8)式左端的W*，w*改用W，z表示，计算完成后再恢复到原来情况．这样就要计算

而

由(7)可知

因此(9)式变为

经过过计算得到:

其中Iαβ为p×p矩阵，若α =β，则位于α行和β列交叉处的元素为1，其余元素为0;若α≠β，则位于α行β和列交叉处的元素为，而在α列和β行交叉处的元素也是，其余元素为0．

所以

因而(10)式就变为

恢复到原来变量，由于M，M'，M″都是不变函数，因而上式变为

上式等于

由于对任意向量α，总有

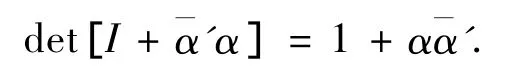
因此上式等于

注意到(11)，而且上式就是(8)式的左端，因此(8)式就化为

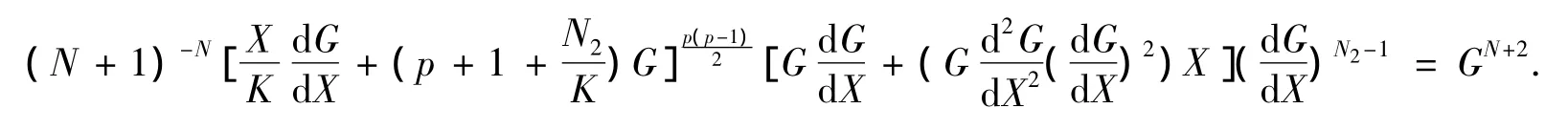
这表示(1)中的复蒙日－安培方程等价于上述的常微分方程．因此问题(1)就等价于下述二阶常微分方程二点边值问题

因此问题(1)的多重强次调和函数解就是

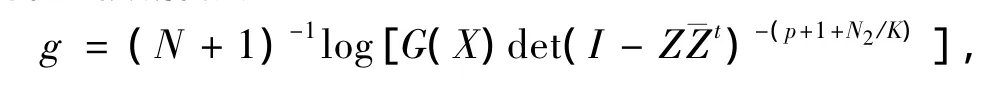
其中G=G(X)满足

而且是问题(14)的解．

3 蒙日－安培方程Dirichlet问题的显式解

在一些特殊情况下，可以求得(14)的显式解．令

把它代入(14)式的常微分方程，然后定出常数A．经计算，得到:

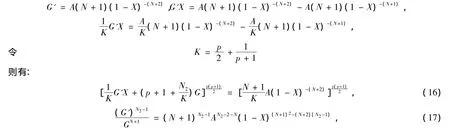
再计算得到:

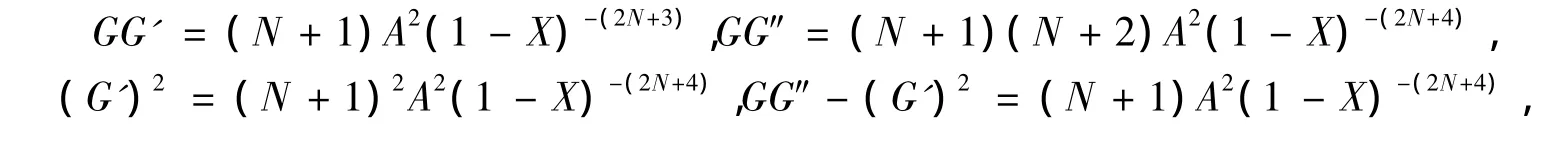
因此有:

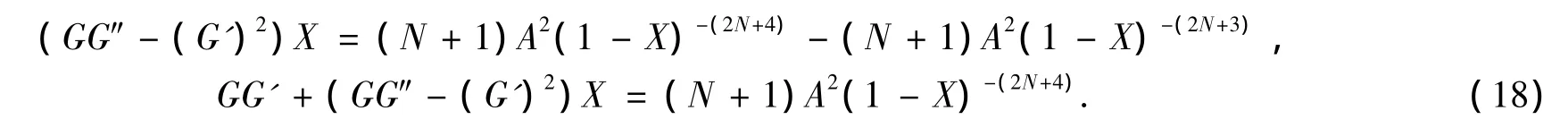
把(15)，(16)，(17)，(18)的结果代入(14)得到:

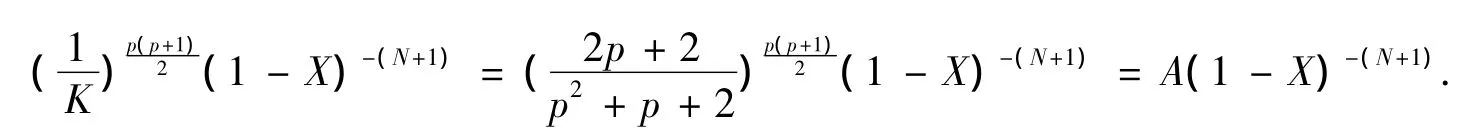
因此必须取

此时，满足(14)中的第一个边界条件，而且有

上式也就是

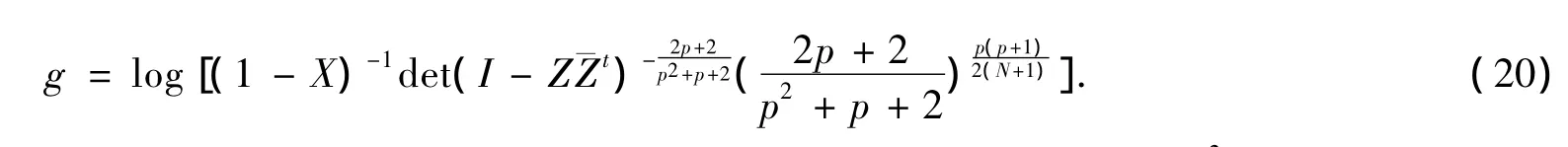
它是问题(1)的多重强次调和函数解，它显然满足问题(1)中的蒙日－安培方程而且．下面证明它也满足边界条件．为此，只要证明下面更一般的定理1就可以了．

是问题(1)的多重强次调和函数解．

证:首先，上述g显然满足(1)中的蒙日－安培方程，而且由．下面只须证明g也满足(1)式中的边界条件．

注1:在问题(14)中的条件“limX→1G(X)=∞”对数值解而言是一个难点．但是可以用下述方法克服之．

注2:参考文献［5］讨论了当N2=1时的问题(1)的解，本文研究了N2为一般情况时问题(1)的解，而且所出现的常微分方程也不同．

注3:这里的Cartan－Hartogs域是华罗庚域的一种，它共有5种［6，7］．它们有一个共同的特点:设华罗庾域的任意一点的坐标为(W，Z)，那么总存在该域的全纯自同构把(W，Z)变成(W*，0)．抓住这个特点可以给华罗庚域一个更为广泛的定义:

注4:本文“数值解探讨(二)”是探讨第二类Cartan－Hartogs域上的复蒙日－安培方程Dirichlet问题的数值解．关于第一类、第三类和第四类Cartan－Harogs域上的复蒙日－安培方程Dirichlet问题数值解的探讨，将分别发表于《数学进展》、《应用数学学报》中文版和《数学物理学报》中文版，有兴趣的读者可以到上述刊物上查找．

这证明了g也满足(1)式中的边界条件．至此，定理1得证．这样，再结合(19)到(20)的叙述，下述定理2成立:

定理2

由(8)可知G(X)必须取正值，所以是

完全确定的．这样问题(14)就变成如下的问题:

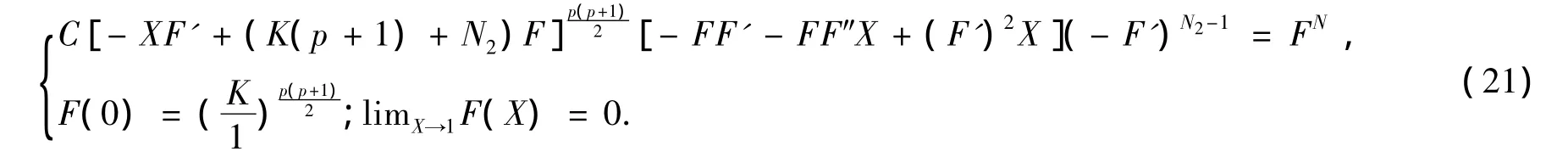
华罗庚域的新定义:设域H是CM+N中的包含原点的不可约有界单连通域，H中的点记为(W，Z)，其中W∈CM，Z∈CN，而且(W，Z)∈H，那么(W，0)∈H．若对H中的任意一点(W0，Z0)，在H的全纯自同构群Aut(H)中存在一个元素F(W，Z)使得不是固定点，则称H为华罗庚域．

这种华罗庚域也称为分片齐性域，在个别情况下H是单片齐性域，即H本身就是齐性域，一般而言，齐性的片数有无穷多个，有时有连续统那么多．在极限情况M=0时，则华罗庚域的定义变成有界齐性域的定义了．因而华罗庚域可以看成是齐性域的推广．

［1］Cheng S Y，Yau S T．On the existence of a complete K hler metric on noncompact complex manifolds and the regularity of Fefferman’s equation［J］．Comm．Pure App．Math，1980，33:507．

［2］Mok N，Yau S T．Completeness of the K hler－Einstein metric on bounded domain and the characterization of domain of holomorphy by curvature conditions［J］．Proc．Symposia Pure Math．，1983，39:41．

［3］Keller H B．Numberical Solution of Two－Point Boundary Value Problems［M］．Philadelphia:Society for Industrial and Applied Mathematics，1976．

［4］殷慰萍．第二类超Cartan域的Bergman核函数［J］．数学年刊，2000，21A(3):331－340．

［5］Zhao Xiaoxia，Yin Weiping，Zhang Liyou．Einstein－Kaehler metric on superCartan domain of the second type［J］．Progress in Natural Science，2004，14(3):201－212．

［6］殷慰萍．华罗庚域研究的综述［J］．数学进展，2007，36(2):129－152．

［7］殷慰萍，赵晓霞，张文娟．华罗庚域的创建与研究［A］．陆启铿，殷慰萍．多复变在中国的研究与发展［C］．北京:中国科学出版社，2009．116－149．