基于偏好信息的实数型不确定交通安全测度研究

王斌

（西南交通大学，四川成都 610031）

基于偏好信息的实数型不确定交通安全测度研究

王斌

（西南交通大学，四川成都 610031）

由于交通安全问题的复杂性和交通安全测度者认识的不确定性，在实数型不确定交通安全测度过程中可能会给出不同形式的偏好信息。针对互反判断矩阵、模糊互补判断矩阵、残缺互补判断矩阵和混合判断矩阵4种测度对象偏好信息，分别采用特征向量法、最小方差法、残缺互补判断矩阵的线性方程组法和混合判断矩阵的线性目标规划法计算出相应的排序向量，然后采用WAA算子合成出每个交通安全测度对象的综合测度值，并排序。算例研究证明该方法的有效性和易操作性。

偏好信息；实数型；不确定；交通安全测度

0 引言

由于交通安全问题的复杂性和交通安全测度者认识的不确定性，不确定交通安全测度问题已成为交通安全评价中的一个新的研究方向。目前，关于方案无偏好的不确定多属性决策问题的研究已经取得了丰富的成果[1-7]。然而，在实际交通安全测度过程中，交通安全测度者通常对交通安全测度对象有一定的主观偏好，即对交通安全测度对象有偏好信息的不确定交通安全测度问题，国内外学者对此研究较少。本文针对基于偏好信息的实数型不确定交通

安全测度问题，提出了一种基于判断矩阵和WAA算子的不确定交通安全测度方法，即对偏好信息分别采用互反判断矩阵、模糊互补判断矩阵、残缺互补判断矩阵和混合判断矩阵4种标度，再分别使用特征向量法、最小方差法、残缺互补判断矩阵的线性方程组法和混合判断矩阵的线性目标规划法计算出各自排序向量，最后采用WAA算子合成出每个测度对象的综合测度值，并通过算例证明该方法的有效性和易操作性。

1 交通安全测度者的偏好信息类型

ij表示交通安全测度者dk认为交通安全测度对象χi优于交通安全测度对象yi的程度，且，则此类信息为互补判断矩阵型偏好信息。

如果交通安全测度者dk根据某一准则或偏好对交通安全测度对象进行两两比较，给出互反判断矩阵Ak=（akij）n×n，其中akij表示交通安全测度者dk认为交通安全测度对象χi优于交通安全测度对象yi的程度，且，则此类信息为互反判断矩阵型偏好信息。如果互补判断矩阵中，既有残缺元素又有非残缺元素，且非残缺元素满足cij+cji=1，cii=0.5，cij≥0，则此类信息为残缺互补判断矩阵偏好信息。

既含有互反判断信息，又含有互补判断信息的矩阵称为混合判断矩阵，该矩阵所反映的信息为混合判断矩阵型偏好信息。

2 基于偏好信息的实数型不确定交通安全测度方法

交通安全测度者在表达交通安全测度信息时，往往以感性认识为判断依据，具有不精确、不完备的特点；同时，交通安全测度的要求又有轻重缓急之分。因而，交通安全测度者常常以互反判断矩阵、互补判断矩阵、残缺互补判断矩阵和混合判断矩阵等偏好形式对交通安全测度对象进行测度，并采用特征向量法、最小方差法、残缺互补判断矩阵的线性方程组法和混合判断矩阵的线性目标规划法对交通安全测度对象进行排序。

2.1 特征向量法

但是，由于交通安全问题的复杂性及交通安全测度者知识水平的影响，在实际交通安全测度中所做出的判断往往是非一致性的，所以式（1）一般不成立。因而可以用下列特征值问题来近似代替式（1）：

式中：λmax——互反判断矩阵A的最大特征值；

ω——A的最大特征值所对应的特征向量，归一化后就是A的排序向量。

由此导出排序向量的方法称为互反判断矩阵排序的特征向量法（CEM）。

为了求得互反判断矩阵A的排序向量ω=（ω1，ω2，…，ωn），可采用下列迭代算法[8]：

（1）任取初始正向量

ω（0）=[ω1（0），ω2（0），…，ωn（0）]∈A，给定迭代精度ε。令k=0。

（2）计算

F（ω）总是越小越好，因此，合理的排序向量ω*应使

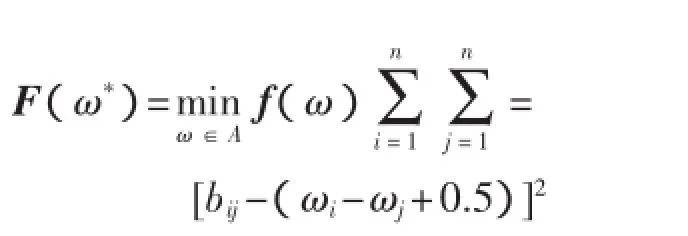
ω为转换矩阵A的排序向量。

2.2 最小方差法

设判断矩阵B是模糊互补判断矩阵，ω=（ω1，ω2，…，ωn）是B的排序向量。如果

则对任意k∈N，有bij=bik-bjk+0.5，故矩阵B是加型模糊一致性互补判断矩阵。如果B不是加型模糊一致性互补判断矩阵，则式（3）往往不成立。为此，引入偏差项，即令

同时构造偏差函数

用构造法解题,关键是构造,它无一定之规,表现出思维的试探性、不规则性和创造性[2]．本题还可通过构造函数y=lnx与y=ax-1或构造函数与y=a来解决．

成立。由此导出排序向量的方法称为模糊互补判断矩阵的最小方差法（LVM）。

设互补判断矩阵B=（bij）n×n，则由LVM求得的排序向量ω=（ω1，ω2，…，ωn）满足[9]：

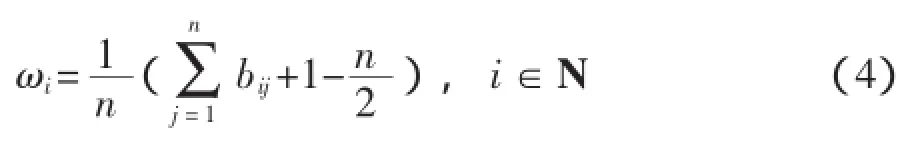
2.3 残缺互补判断矩阵的线性方程组法

对于某一交通安全测度问题，交通安全测度者利用互补标度在某一准则下对测度指标进行两两比较，并构造残缺互补判断矩阵C=（cij）n×n。其中C中的残缺元素cij用未知数χ表示，且相应的cij用1-χ表示。

对于残缺互补判断矩阵C=（cij）n×n构造一个辅助矩阵=（）n×n，其元素为得到一个线性方程组，并解之，可得残缺互补判断矩阵C的排序向量ω=（ω1，ω2，…，ωn）。

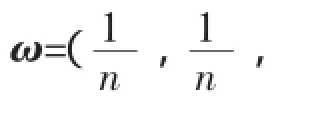
2.4 混合判断矩阵的线性目标规划法

当C=（cij）n×n是一致性混合判断矩阵时，其中的互反判断信息满足：

其中的模糊互补判断信息满足：

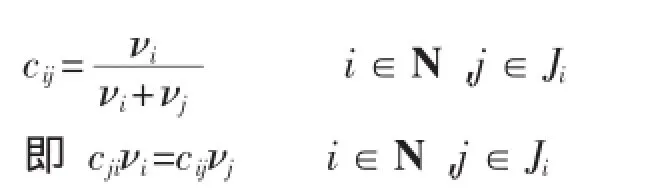
由于交通安全测度者在实际测度时所给出的判断矩阵常常是非一致性的，νi=cijνj和cjiνi=cijνj一般不成立。为了刻画此非一致性，引入偏差函数：

为了得到合理的排序向量ν=（ν1，ν2，…，νn），偏差函数fij的值总是越小越好。求解最佳排序向量ν=（ν1，ν2，…，νn），构造下列多目标最优化模型

假设所有的交通安全目标函数都是公平竞争的，且每个交通安全目标函数fij的期望值都是0，所以可以将上述模型转化为

tij——dij的权系数。

解此线性目标规划模型，可以得到混合判断矩阵C的排序向量ν。

3 算例

路口渠化是提高道路通行能力的重要措施，也是提高交通安全水平的重要手段。渠化路口是指依据《城市道路设计指南》，根据路口流量和基本特征，对车辆、行人作合理分离、导流等设计，并以标线和其他物理设施等形式实施的路口。渠化是否合理的判断依据是：（1）路口渠化时，左转、直行、右转进口道数量是否与相应方向的交通量一致，用U1表示；（2）路口中央是否有导流标线，用U2表示；（3）两相位控制时，左转车道是否有等待位置指示线，用U3表示；（4）根据视距三角形原理，是否保证了足够视距，用U4表示；（5）信号周期、绿信比和相位差3个参数设置是否符合路口交通流的实际情况，用U5表示；（6）路口渠化与信号控制参数设置是否协调，用U6表示；（7）渠化标志是否符合规范，用U7表示；（8）渠化标线是否符合规范，用U8表示。现有4位交通安全测度者dk（k=1，2，3，4）根据上述8个指标对4个路口χi（i=1，2，3，4）进行打分（范围从0分到100分）测度，其测度结果如表1～表4所示。

同时这4位交通安全测度者对上述8个指标利用0.1～0.9五标度或1～9标度进行两两比较并构造判断矩阵Bk（k=1，2，3，4）（它们分别为互反判断矩阵、模糊互补判断矩阵、残缺互补判断矩阵和混合判断矩阵），即：

表1 测度者d1给出的测度矩阵R1

表2 测度者d2给出的测度矩阵R2

表3 测度者d3给出的测度矩阵R3

表4 测度者d4给出的测度矩阵R4

试对这4个路口交通安全状态进行测度。

（1）计算交通安全指标判断矩阵的排序向量。

利用特征向量法求出B1的排序向量：

利用模糊互补判断矩阵排序的最小方差法求出B2的排序向量：

利用残缺互补判断矩阵排序的方法求出B3的排序向量：

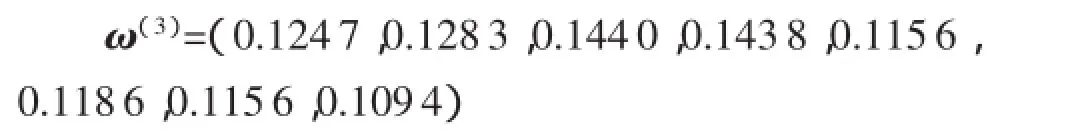
利用混合判断矩阵排序的线性目标规划法求出B4的排序向量：

（2）利用WAA算子对交通安全测度矩阵Rk中第i行的交通安全指标值进行加权合成，得到交通安全测度者dk所给出的测度对象χi的综合交通安全测度值（ω（k））。

（4）利用CWAA算子对4位交通安全测度者给出的测度对象χi的综合交通安全测度值z（k）i（ω（k））合成。

（5）按zi（λ，w）值大小排序。

4 结束语

针对基于偏好信息的实数型不确定交通安全测度问题，本文给出了互反判断矩阵、模糊互补判断矩阵、残缺互补判断矩阵和混合判断矩阵4种偏好信息类型，分别采用特征向量法、最小方差法、残缺互补判断矩阵的线性方程组法和混合判断矩阵的线性目标规划法求解。该方法计算简单，易于上机实现，为解决多种偏好信息形式的实数型不确定交通安全问题提供了一个新的途径。

[1]熊文涛，刘三阳，史加荣．不确定型多属性决策的一种新方法[J]．系统工程与电子技术，2005，27（5）：841-843.

[2]许叶军，达庆利．一种不确定型OWGA算子及其在决策中的应用[J]．系统工程与电子技术，2005，27（6）：1038-1040.

[3]许叶军，达庆利．不确定型多属性决策的权系数确定及其应用[J]．系统工程理论方法应用，2005，14（5）：434-436.

[4]Yao SB，Yue C Y．Method formultip le attribute decisionmaking under risk based on synthetic weighting[J]．Systems Engineering and Electronics，2005，27（12）：2047-2050.

[5]Zhou H G，Liu S Y．Method of uncertainmulti-attribute decision-making based on quadratic programm ing and relative superiority degree[J]．Systems Engineering and Electronics，2007，29（4）：559-562.

[6]HuangW Q，Yao SA，Guo Y J．Dynamic comprehensive evaluation model of incomplete index preference information and its application[J]．Journal of Northeastern University（Natural Science），2011，32（6）：891-894.

[7]Cai Z Y，Cai ZQ．Group-decision making withmulti-level using vague set under fuzzy preference environment[J]．Journal of Huazhong University of Science&Technology：Natural Science，2010，38（9）：68-71.

[8]徐泽水．互补判断矩阵的两种排序方法——权的最小平方法及特征向量法[J]．系统工程理论与实践，2002，22（7）：71-75.

[9]徐泽水．模糊互补判断矩阵排序的最小方差法[J]．系统工程理论与实践，2001，21（10）：93-96.

Research on real uncertain traffic safety measurement based on preference information

WANG Bin
（Southwest Jiaotong University，Chengdu 610031，China）

Due to the complexity of traffic safety and the uncertainty of traffic measurement，the different forms of preference information may be given in real uncertain traffic safety measure process.According to four kinds measuring object preference information of reciprocal judgment matrix，fuzzy complementary judgment matrix，incomplete complementary judgment matrix and hybrid judgment matrix，eigenvector method，least square method，incomplete matrix method and hybrid matrix linear goal programming method are used to calculate the corresponding sorting vector，then the integrated values of each traffic safety measure object are synthesized with WAA operator and sorted.The result of case study shows that the method is effective and easy to operate．

preference information；real；uncertainty；traffic safety measure

U491；O213.2；TM930.114；TP274+.2

A

1674-5124（2013）02-0019-05

2012-07-09；

：2012-08-30

王斌（1969-），男，四川剑阁县人，讲师，博士研究生，主要从事交通运输安全工程研究。