墙土体参数对地下连续墙基础沉降数值模拟的影响

舒中潘，钱江澎，唐晓玲

（四川省地质工程勘察院，成都 610072）

数值模拟地下连续墙基础作为锚碇基础在我国应用以来，不少学者也开始了其沉降计算方法的研究。同济大学的张琦以上海同济大学图书馆扩建工程为对象，以现场实测数据为依据，引用Mindlin 公式，提出了实用沉降估算公式[1]。上海华东建筑设计研究院的王卫东在文献[2]中提出了用Poulos 弹性理论法进行地连墙基础的沉降计算。同济大学工程的季明李桂花提出了由地连墙-桩-箱或筏所构成的复合基础的二阶段沉降计算方法[3]。美国乔治亚理工学院土木与环境工程系的常红和兰州铁道学院土木工程系的郑越通过研究模型试验中地连墙在竖向受荷时墙顶的沉降特性，推导出一字形墙的沉降计算公式，提出了采用增大系数计算异型地连墙基础沉降的方案[4]。

地下连续墙作为黄土地区桥梁承受竖向力的基础类型，在工程中还未有应用的报道。目前，黄土地区大跨度桥梁的基础形式非常单一，然而，黄土层所具有的平面均质性，直立性以及地下水位较低等特点，使地下连续墙应用于黄土地区大跨度桥梁基础有着广阔的前景。本文结合晋陕边界黄土高原上省重点工程国道209 线河津至临猗段K23+385m处天桥，采用Marc 软件对黄土地区大跨度桥梁地下连续墙基础沉降进行数值模拟研究[5]，并分析墙土体参数对沉降的影响。

1 桥址区工程地质条件

拟建天桥地处山西省万荣县高村，桥址区的地貌单元属峨眉台塬风积黄土地貌，地形平坦，地面标高介于727.92～729.20m 之间，高差1.28m。地层该工程场地50m 深度范围内未见地下水。根据桥台位置附近的剖面出露，该处黄土与古土壤分层沉积，为黄土高原第四纪黄土与古土壤交替沉积的典型地层，土体物理力学性质见表1。

图1 地下连续墙平面示意图

图2 三维实体

图3 Z方向位移

2 计算模型

2.1 几何模型

实例所研究地下连续墙基础深h=18m，平面呈闭合正方形,外轮廓边长l=7m，墙宽w=0.8m（图1）。

2.2 材料本构模型

有限元数值计算结果精度主要取决于本构模型的合理性和计算参数的准确性。实例墙采用弹性体分析、对桩周土体采用弹塑性分析。Marc 中提供的屈服准则有Von.Misses 屈服准则，Mohr-Coulomb 屈服准则等，比较适用于岩土的是Mohr-Coulomb 屈服准则。经过对比分析本文采用线性Mohr-Coulomb 屈服准则。

2.3 单元网格划分及边界条件确定

利用对称性取1/4 部分进行建模分析。本例的计算边界确定为：在x、y 方向取距原点12.5 倍的墙宽，即lx=ly=10m，作为计算模型x、y 向的边界；墙底以下取一倍的墙深作为计算模型的下界，即lz=-36m。本例采用6 面体8 节点实体单元模拟墙土体，三维实体模型如图2 所示，实体单元共计14 212个，结点总数为17 554个。

在模型的两个侧界和下界之处，土体受地连墙的影响甚微，该三个面上所有节点的x、y、z 方向上位移均为零；在xz 对称面上所有节点y 方向位移为零；在yz 对称面上所有节点x 方向位移为零；所有单元均施加重力荷载；地连墙顶面单元上受外加均布应力。

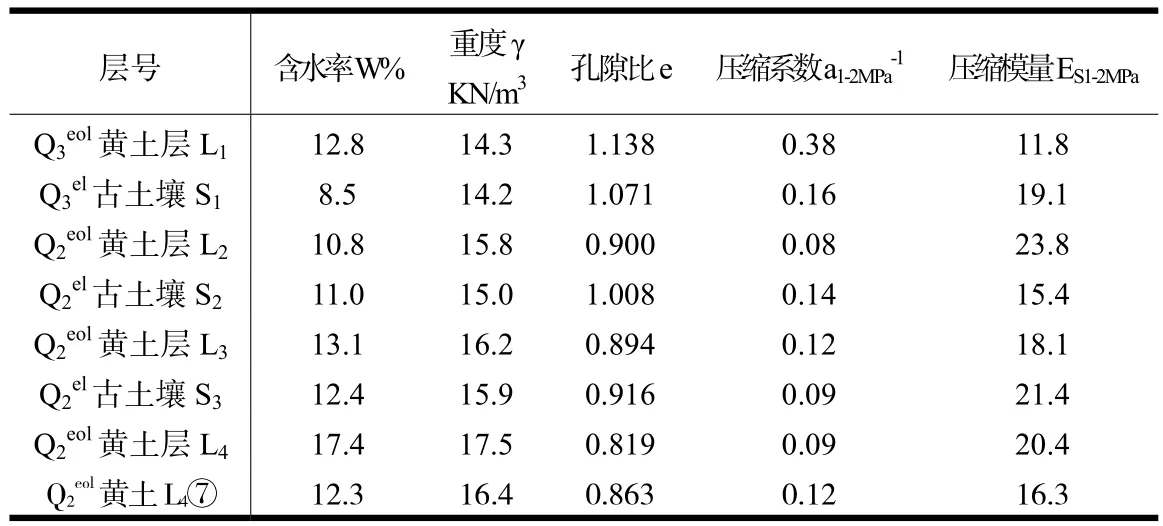
表1 桥址区土体物理力学性质

2.4 计算参数

地连墙及墙周土体计算参数见表3。考虑到施工顺序并结合实测工况的沉降值，将墙顶竖向荷载分为5个工况，即5 级荷载施加，大小从5 625KN 到20 191KN。

表2 计算参数的选取

表3 墙顶节点计算值、实测值

3 计算成果

3.1 计算值与实测值的比较

地连墙基础在最后一级荷载作用下竖向位移云图如图3 所示。具体每工况沉降计算值和实测值如表3所示，对比Q-S 曲线如图4 所示。

根据以上图表，计算值和实测值均显示，随着结构荷载的增加，基础沉降值也随之增大，当施加在墙顶的竖向荷载较小时，计算值和沉降值相当接近，随着荷载的增加两者沉降差值有所加大，但总体吻合较好。在最后一级荷载作用下计算值要大于沉降值约1.71mm，占计算值的10%左右，其原因主要是在数值计算过程中，由于无法通过试验得出各古土壤层强度参数值，按其上层黄土参数值进行模拟计算，从而忽略了各古壤层强度优越性。

3.2 土体变形模量 E0的影响

土体的变形模量在地基沉降的数值计算中尤为重要，本节取变形计算深度范围内变形模量的当量值E进行分析，分别取E为10MPa、20MPa、30MPa 进行数值计算。

由图5 (a)、(b)、(c)可以清楚的看出在其它参数不变的情况下，对于3 种不同尺寸的地连墙基础，其沉降随土体模量的减小而显著增加。3 种墙体尺寸情况下，墙周土变形模量10MPa 至少是30MPa 基础沉降的3 倍以上，这说明墙周土体的变形模量对基础沉降的影响相当大。因此，闭合形地连墙基础应用于较好的黄土地层或古土壤中，会有较大优越性。

3.3 土体泊松比ν 的影响

无论是现场试验还是室内试验，土体泊松比是最难确定的参数之一，也是基础沉降计算必不可少的参数之一，但泊松比对沉降计算的影响也是大多数研究者所关心的问题之一。通常根据土基土的侧压力系数推算ν 值，由于本论文无此试验数据，故参照文献[6]根据经验值取0.2、0.3、04 进行分析。

图4 计算值与实测值的比较

图5 不同墙体尺寸下土体变形模量对沉降的影响

图6 不同墙体尺寸下土体泊松比对沉降的影响

由图6(a)、(b)、(c)可以看出，总体上泊松比对沉降的影响不大，但随着泊松比的减小，基础沉降有所增加。在最小墙体尺寸情况下，土体泊松比对地连墙基础沉降有一定的影响，3 种泊松比的最大沉降差在7%左右。随着墙体尺寸加大，泊体比对基础沉降的影响逐渐减小，在最大尺寸墙体情况下，3 种泊松比的最大沉降差降到3.8%左右。

图7 不同墙体尺寸下土体泊松比对沉降的影响

3.4 墙土间摩擦系数对基础沉降的影响

地连墙侧壁与墙侧土之间的作用力属于摩擦力，即墙侧摩阻力，因而从本质上来说，墙侧摩阻力的大小取决于墙侧土作用于地下墙的有效法向应力的大小及墙与土之间的接触情况和摩擦系数。本节通过取墙土之间不同的摩擦系数来进行数值计算，以分析其对基础沉降的影响。

图7(a)、(b)、(c)显示了土体模量在E=20MPa，摩擦系数分别为0.1、0.3、0.6时各种墙体尺寸的Q-S曲线。可以看出，摩擦系数越大，基础沉降值越小，表明基础侧摩阻力分担的荷载随着摩擦系数的提高而有所增加，但通过提高摩擦系数减小基础沉降的效果并不明显，沉降值的减幅均在10%以内。

4 结论

1）现场实例计算值与实测值表明所建模型合理可行。

2）墙周土体的变形模量对基础沉降的影响相当大。其沉降随土体模量的减小而显著增加，3 种墙体尺寸情况下，墙周土变形模量10MPa 至少是30MPa 基础沉降的3 倍以上。

3）计算结果表明泊松比对地连墙基础沉降的影响相当微弱，因而在进行数值模拟计算时，其取值在经验值范围内，对计算结果基本无影响。

4）墙土间摩擦系数与众多因素有关，确定其具体值有较多的难度，但通过数值模拟分析，在该黄土地区墙土间摩擦系数的提高对减小基础沉降效果并不明显，根据前人研究资料及经验，摩擦系数取0.3左右较为符合实际情况。

[1]陈火红.Marc 有限元实例分析教程[M].北京：机械工业出版社，2002.

[2]张伟，周锡祢，刘海笑，张建辉.滩海桶形基础平台三维有限元静力分析[J].中国海洋平台,2001.16(1)：9～14

[3]沙迎春，吴中如.红水河[J].2002，22(2)：61～64

[4]周敏.利用Marc 前处理功能建立岩土地基的有限元模型[J].西部探矿工程,2004，No.6：3～7

[5]苏静波，尹建兵，董兴平.岩土体的本构模型在Marc 中的实施[J].盐城工学院学报(自然科学版).2005，18(1)：6～8

[6]Jacob J.B Esterhuizen，J.Michael Duncan,Consititutive Behavior of Geosynthetic Interfaces,Journal of Geotechnical and Geoenvironmental Engineering,2001,10

[7]殷宗泽、朱汪、许国华.土与结构材料接触面的变形及其数学模拟[J].岩土工程学报，1994.，16(3)∶

[8]刘成宇.土力学[M].北京：中国铁道出版社，2002.