ρ混合序列的Hajek-Renyi型不等式
2013-07-07万英
万英
(湖北大学 数学与计算机科学学院,湖北 武汉 430062)
ρ混合序列的Hajek-Renyi型不等式
万英
(湖北大学 数学与计算机科学学院,湖北 武汉 430062)
将独立随机变量序列的Hajek-Renyi型不等式推广到ρ混合序列,并应用此不等式研究其强大数定律。
ρ混合序列;Hajek-Renyi型不等式;强大数定律
1 引言及预备知识
设{bn,n≥1}为一非降的正实数列,Hajek和Renyi[1]于1955年证明了下面的不等式:设{Xn,n≥1}是独立随机变量序列,且有有限的二阶矩,则对任意的ε>0和任意的正整数m<n,有

自从提出Hajek-Renyi型不等式之后,有很多学者对此产生了浓厚的兴趣,研究了将独立随机变量序列的Hajek-Renyi型不等式推广到NA序列、ϕ混合序列、ϕ~序列等。本文主要是将上述独立随机变量序列的Hajek-Renyi型不等式推广到 ρ混合序列,应用这个不等式进一步研究强大数定律以及上确界的可积性。
设{Xn,n≥1}是定义在概率空间(Ω,A,P)上的随机变量序列,记为σ域,记Lp(A)为所有A可测且 p阶矩存在的随机变量全体。在A中给定σ域 F和 R,令 ρ(F,R)=sup{corr(X,Y):X∈L2(F),Y∈L2(R)},其中corr(X,Y)= |EXY-EXEY|/为相关系数,对。
定义1 对随机变量序列{Xn,n≥1},如果 ρ(n)↓0(n→∞),则称{Xn,n≥1}为 ρ混合序列。
ρ混合序列概念由Kolmogorov和Rozanov[2]于1960年引入。由定义1可以看出 ρ混合序列是一类应用非常广泛的随机变量序列,通常的独立随机变量序列可以看成是 ρ混合序列的特殊情形。
引理1[3]设为 ρ混合序列其中 p,q≥1且满足1/p+1/q=1,那么
2 主要结果及证明
定理1 设{Xn,n≥1}为 ρ混合序列,满足为一非降的正实数列,则对任意的ε>0和任意的正整数m<n,有
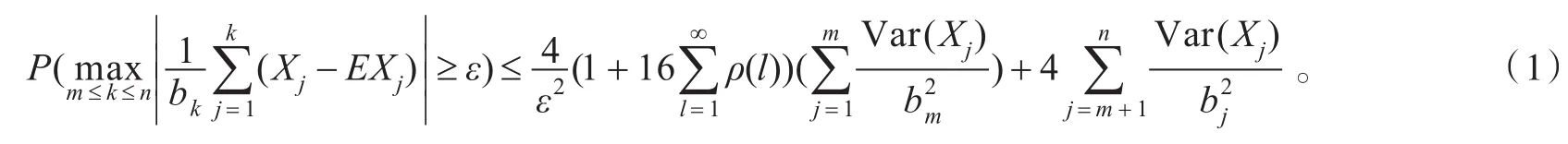



[1] Hajek J,Renyi A.A generalization of an inequality of Kolmogorov[J].Acta Math Acad Sci Hungar,1955(6):281-284.
[2] Kolmogorov A N,Rozanov U A.On the strong mixing conditions of a stationary Gaussian process[J].Prob Theory Appl,1960,2(1):222-227.
[3] 林正炎,白志东.概率不等式[M].北京:高等教育出版社,2006.
Hajek-Renyi Inequality forρ-mixing Sequences
WAN Ying
(School of Mathematics and Computer Science,Hubei University,Wuhan 430062,Hubei,China)
Promotes the Hajek-Renyi inequality of independent random variable sequence proved by Hajek and Renyi in 1955 to theρmixing sequence,then study the strong law of large numbers with applying this inequality.
ρ-mixing sequences;Hajek-Renyi inequality;strong law of large numbers
O211.4
:A
:1673-0143(2013)01-0043-04
(责任编辑:强士端)
2012-12-16
万 英(1988—),女,硕士生,研究方向:数理统计。
