基于初始聚类中心优化和维间加权的改进K-means算法

王 越，王 泉，吕奇峰，曾 晶

(重庆理工大学计算机科学与工程学院，重庆 400054)

K-means算法是最常用的聚类算法之一，是一种基于划分的聚类算法，具有聚类速度快、易实现、对大型数据集能进行高效分类的特点。但是K-means算法也有其不足，例如传统K-means算法的初始聚类中心点选择是随机的，不同的初始聚类中点心会使得到的聚类结果不同，甚至可能无法得到有效的聚类结果［1-2］。所以如何选择合理的初始聚类中心点，使得聚类的结果准确、稳定、有效，是一个重要的研究方向［3］。目前，已有大量的文献针对K-means算法的初始聚类中心点的选取进行了研究，例如:基于样本点之间最大最小距离的选择方法［4］;将随机选择初始聚类中心点的过程重复多次，然后取最优结果的择优法［5］;基于簇密度的密度法［6］;基于遗传算法寻找初始聚类中心点的遗传法［7-8］;递归法［9］;基于种群的启发式搜索算法［10］等。这些算法都能有效提高 K-means算法聚类的准确性，但是却需要反复进行大量的计算，增加了算法的时间复杂度。

本文提出一种新的基于样本点之间距离的初始聚类中心选择算法，不需要进行大量的计算便能得到合理的初始聚类中心点。实验结果表明，改进后的算法比传统的K-means算法有更高的准确性与稳定性。

1 改进的K-means算法的基本思想

1.1 初始聚类中心点选取的算法

令样本数据集合 S={x1，x2，…，xn}，传统的K-means算法是从S中随机选择k个样本点，每一个样本点代表一个聚类的质心。这样导致了聚类结果的波动性，使得聚类结果不稳定且平均准确率不高。

改进初始聚类中心点选取的思路:

1)计算数据集所有样本点两两之间的距离。K-means算法用2个样本点之间的欧式距离代表2点的相似程度，距离越小说明样本点之间的相似度越高。2点间的欧式距离可定义为

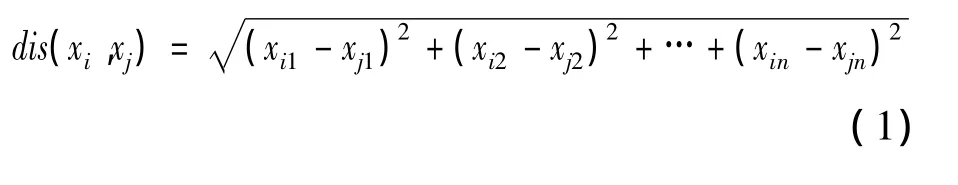
其中:xin为样本点xi第n维的数据对象;xjn为样本点xj第n维的数据对象。

2)计算所有样本点之间的平均距离，可定义为

3)将与样本点xi(其中1≤i≤n)的距离小于平均距离 mDis的样本点 xj(1≤j≤n，j≠i)记录下来，称其为邻近点，并计算出xi的邻近点数量。当所有样本点的邻近点统计结束后，将它们按邻近点的数量从高到低排序。邻近点数量最多的样本点作为第1个聚类中心点。然后继续往下查找。若邻近点数量第2的点是已有初始聚类中心的邻近点则忽略，继续往下查找，直到找到第m个点不是已有聚类中心点的邻近点，则将它作为聚类中心点。反复进行这个过程，直到找到k个初始聚类中心点。这样找到的初始聚类中心点能较好地反映出数据对象的分布，并且能保证找出的k个初始聚类中心点不会过于相近而导致聚类效果不佳。

1.2 样本点维间加权

由于数据集中的不同类的样本点可能因为距离比较近而出现部分样本点有交叠的现象，这样由传统的K-means算法进行聚类时效果会不理想。由于K-means算法采用欧氏距离来表示样本点之间的相似程度，研究式(1)可以发现，如果放大样本点之间差异最大的维度，其他维度保持不变，那么计算出的结果中不同类的样本点之间的距离变大的幅度会比相同类的样本点之间的距离变大的幅度要大一些。因此，对差异最大的维进行加权以后，不同类样本点之间的距离便会比相同类样本点之间的距离拉得更开，从而使聚类的准确度提高。

可通过下述方法找到样本点之间差异最大的维。

用DIM(i)avg表示第i维的平均值，即

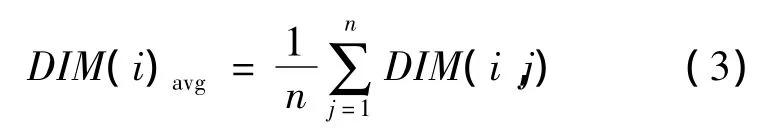
其中:j表示第几个样本;DIM(i，j)表示第j个样本点的第i维的值。然后计算第i维上各样本点的值与该维平均值的差，再求和。可表示为

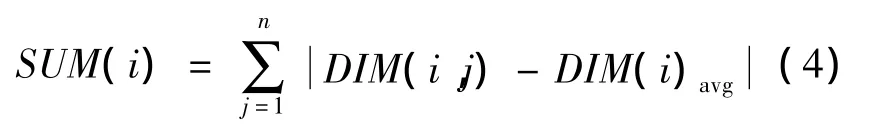
通过对比各维经过上述操作后得到的结果，最大的维便是差异最大的维。

2 改进K-means算法的流程描述

令样本数据集 S={x1，x2，…，xn}，需要将该样本集聚为K类。

改进后的K-means算法流程:

输入:样本数据集S，聚类个数K。

输出:K个聚类。

1)获取样本数据集S，找到样本点之间差异最大的维，并进行加权操作。

2)根据式(1)计算出数据集中样本点两两之间的距离dis(xi，xj)，并保存在n×n的表中。

3)根据式(2)计算出样本点之间的平均距离mDis。

4)将与样本点xi(其中1≤xi≤n)的距离小于mDis的样本点 xj(其中1≤j≤n，j≠i)记录下来，令它们为xi的邻近点，并计算出每个样本点的邻近点的数量，保存在邻近点表中。

5)将样本点x1，x2，…，xn按邻近点数从高到低排列，邻近点最多的样本点作为第1个聚类中心点。

6)依次往下查找邻近点表，若该点是已有初始聚类中心的邻近点则忽略，继续查找邻近点表，直到找到一个样本点不为已有聚类中心点的邻近点，则将它作为另一个聚类中心点。

7)重复步骤6)直到找到第k个聚类中心点。

8)进行聚类运算后，将样本点加权的维还原，并输出实验结果。

3 改进的K-means算法的实验结果与分析

为了考察改进K-means算法的有效性，本文选择用于测试算法性能的UCI数据库中的Iris数据集进行实验。

Iris数据集是被公认为用于数据挖掘的最著名的数据集，它包含3种植物种类，即setosa、versicolor、virginica，每种各有50个样本。它有4个属性:花萼长、花萼宽、花瓣长、花瓣宽。该数据集的数据特点是:第1类样本点与其他样本点离得较远;第2类样本点和第3类样本点离得很近，并且有一些交叠。

使用经典的K-means算法在Iris数据集上进行实验，得到实验结果如表1所示。

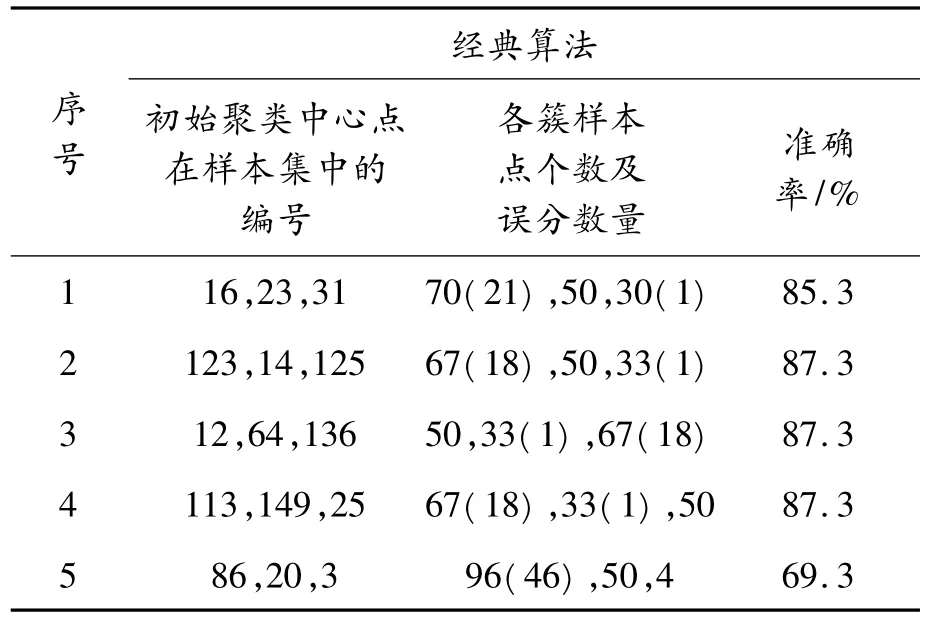
表1 经典算法的实验结果

使用改进后的K-means算法在Iris数据集上再次进行实验，得到实验结果如表2所示。

实验结果表明:经典的K-means算法受初始中心点的影响较大，经过5次实验最好的情况下正确率为87.3%，最差的情况下正确率仅为69.3%。

改进后的算法当样本点差异最大的维加权的系数ω=1，即保持原样本点各维的值不变的时候进行2次实验，虽然准确率相对传统的K-means算法最好的情况没有提高，但是改进后算法的结果稳定，且与传统算法中最好的情况下得准确率相同。当加权系数ω=2时，即放大了样本点之间差异最大的维，发现得到的结果的准确率与不进行加权之前相比有所提高。当加权系数ω=5时，聚类结果的准确率比ω=2时又有所提高，说明对样本点间差异最大维进行加权再进行聚类的方法是可行的，而且ω=2时没有达到改进算法的最大正确率。当加权系数ω=10时，实验的结果和ω=5时一样，准确率不再提高，说明已达到改进后算法的最大正确率92%。

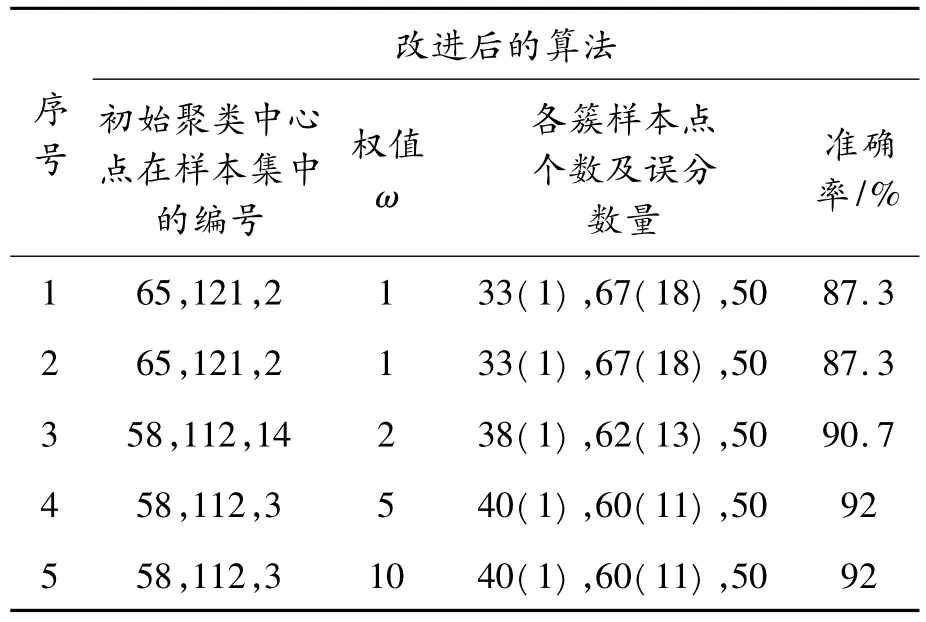
表2 改进后算法的实验结果

4 结束语

K-means算法计算速度快、资源消耗小，是一种应用广泛的聚类算法。传统的K-means算法由于初始聚类中心点的选取是随机的，造成了聚类结果的不稳定。改进的算法改进了初始中心点的选择方法，并且对样本点之间差异最大的维进行加权操作。实验证明改进后的算法能找到合适的初始聚类中心点，并且有效提高了算法聚类的准确率。不足之处是需要人工进行多次实验才能确定权值何时才是最优，如何自动获得最优的权值将是下一步的研究方向。

［1］HAN Jia wei，KAMBER M.Data Mining Concepts and Techniques［M］.［S.l］：Morgan Kaufman Publishers，2001.

［2］韩存鸽.聚类挖掘在高校图书馆管理系统中的应用［J］.重庆理工大学学报：自然科学版，2012(11)：83-87.

［3］顾洪博，张继怀.聚类算法初始聚类中心的优化［J］.西安工程大学学报，2010，24(2)：222-226.

［4］连凤娜，吴锦林，唐琦.一种改进的K-means聚类算法［J］.电脑与信息技术，2008，16(1)：38-40.

［5］曹文平.一种有效K-均值聚类中心的选取方法［J］.计算机与现代化，2008(3)：95-97.

［6］袁方，周志勇，宋鑫.初始聚类中心优化的K-means算法［J］.计算机工程，2007，33(3)：65-66.

［7］赖玉霞，刘建平，杨国兴.基于遗传算法的K均值聚类分析［J］.计算机工程，2008，34(20)：200-202.

［8］路彬彬，贾振红，何迪，等.基于新的遗传算法的模糊C均值聚类用于遥感图像分割［J］.激光杂志，2010(6)：15-17.

［9］李业丽，秦臻.一种改进的K-means算法［J］.北京印刷学院学报，2007，15(2)：63-65.

［10］孟岩，刘希玉，刘艳丽.一种基于蚁群算法的K-means算法［J］.计算机工程与应用，2008，44(1)：179-182.