基于环形球栅的扭矩传感器

周 俊

(重庆大学光电技术及系统教育部重点实验室，重庆 400044)

在日常生活和工程实际中，机械构件的主要变形形式是扭转，因此扭转测量的需求十分广泛，其中轴的扭转测量最为常见。扭矩作为反应机械轴扭转程度的机械量，是旋转动力传动系统中十分重要的性能参数［1］。在工程实际中，扭矩不仅被作为机械状态监测和故障预警的重要参数，还被作为系统设计与改进的参考依据［2］。

目前扭矩测量的方法很多［3-4］，主要可以分为3类:测应变、测转角、测反作用力［5］。但是它们都存在器件老化、工作寿命短、对工作环境要求高等缺点，在强冲击、高温、腐蚀、振动等极端环境中难以实现长期不间断的扭矩测量。针对这一工程实际应用需求，本研究提出了一种采用环型空间阵列和磁电式检测器的非接触式扭矩测量方法，并分别设计了基于交流和直流激励的2种传感器，具有抗电磁干扰、抗冲击、耐振动、防油、防尘等特点，可实现极端环境下机械传动系统的动态特性测量［6-7］。在直流激励下，信号处理简单，但是信号幅值和频率依赖于转轴转速，传感器只能测量动态扭矩;在交流激励下，虽然可实现静态和动态测量，但是传感器的输出信号较小，而且单一读数头可能引入随机性误差。针对这些不足，本研究设计了一种采用交流激励的测量头对称的非接触式电磁扭矩传感器，可同时实现静态和动态的扭矩测量，具有输出信号较强、整体可靠性高、工作寿命长等特点。

1 扭矩测量的机械原理

在机械系统中，以扭转为主要变形的杆件称为轴。如图1所示，当轴扭转时，依据力偶平衡方程，其横截面内的内力偶矩与外力偶矩相等，其内力偶矩称为扭矩。

图1 圆轴扭转示意图

圆轴扭转的平面假设:圆轴各个横截面变形后仍保持为平面，形状和大小不变，半径保持为直线，并且相邻两横截面间的距离不变［8］。根据平面假设，扭转变形中圆轴的横截面就像刚性平面一样，绕轴线旋转了一个角度。在材料力学中，将圆轴旋转时任意两横截面产生的相对转角称为扭转角φ，则距离为l的2个横截面之间的相对扭转角为

式中:G为剪切弹性模量;T为两截面微元间的扭矩;Ip为横截面对圆心的极惯性矩。

实心圆轴横截面的极性惯性矩IP计算公式为

其中d为实心圆轴横截面的直径。

将式(3)代入式(2)可得

由式(4)可知，转轴受力矩作用时其上两截面的相对扭转角与扭矩成正比，因此可以通过测量扭转角来测量扭矩。

2 环形球栅传感器理论模型的建立

传感器理论模型如图2所示，由激励线圈A、感应线圈B、励磁铁心和可动小球构成，小球的运动轨迹垂直于纸面方向。

图2 传感器理论模型示意图

依据法拉第电磁感应定律可知:当穿过闭合回路所围面积的磁通量发生变化时，不论这种变化由什么原因引起，回路中都会形成感应电动势，且此感应电动势正比于磁通量对时间变化率的负值，即

式中:k为比例系数，其值取决于各量所用单位;ε为感应电动势;Φ为磁通量。在国际单位制中，式(5)写为

在图2中，激励线圈加载正弦变化的激励电流后，在励磁铁芯中产生不断变化的磁场，通过感应线圈的磁通量也不断变化，根据式(6)感应线圈中将产生感应电动势。

依据比奥-萨法尔定律，空间任意一点，电流所建立的磁感应强度都与该电流成正比，所以该电流产生的磁场穿过线圈的磁通量也必然与该电流大小成正比，即

式中M是互感系数，与线圈的形状、大小、匝数、相对位置以及周围磁介质的磁导率有关［9］。联立式(6)和式(7)可得

从模型中可知:2个线圈的大小、形状、匝数、相对位置都不会变化，唯一可变的是周围介质的磁导率，主要是铁芯缺口处的磁导率。该处磁导率由气隙和钢球的磁导率决定，可以将缺口处的磁导率等效为一种材料的磁导率，等效之后磁路的磁阻不变［10］，即

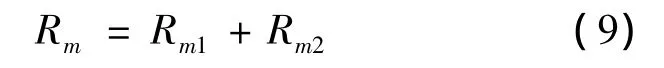
式中:Rm为等效后的磁阻;Rm1表示气隙磁阻;Rm2表示小球磁阻。

依据磁阻定义有

式中L、S、μ分别表示励磁铁芯缺口对应部分的长度、横截面积和磁导率。

空气的磁导率很小，小球的磁导率比较大，整体磁导率主要取决于缺口处小球的体积。用L1表示等效后气隙的长度，L2表示等效后小球材料的长度，V1表示缺口处的体积，V2表示缺口处小球的体积，可得到:

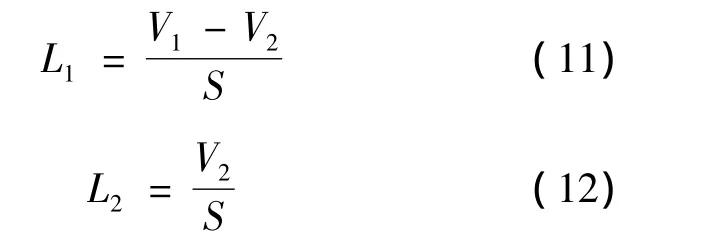
由于 L=V1/S，显然 L1、L2满足 L1+L2=L。联立式(10)～(12)可得

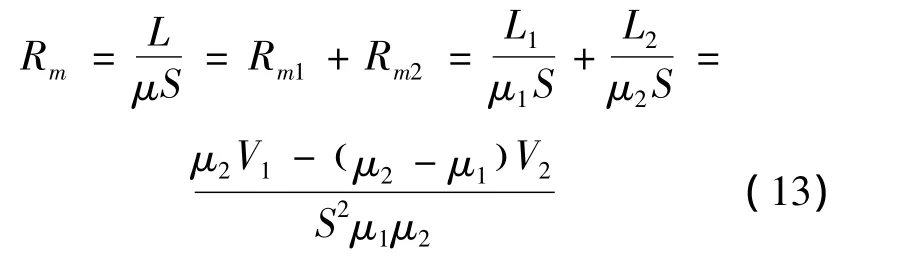
式中μ1、μ2分别为铁芯缺口处气隙的磁导率和小球磁导率。

由于小球的磁导率μ2远大于空气的磁导率μ1，式(13)可简化为

由式(14)可求得

其中μ1、V1为常数。从式(15)可以看出等效磁导率是小球在铁芯缺口处体积V2的函数，令式(15)化为

由于线圈的大小、形状、匝数、相对位置都不会变化，依据比奥-萨法尔定律、磁通量定义以及互感公式可知互感系数M与磁导率成正比，即

其中k为比例系数。

激励线圈的激励电流为i=Imsin(ωt)，联立式(7)和(17)有显然，磁通量 Φ是x的函数。联立式(8)和式(18)，可得

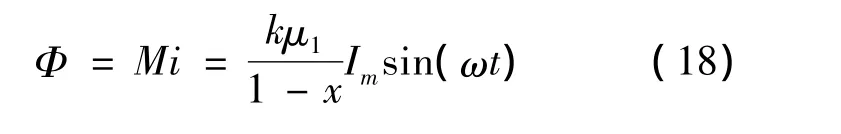
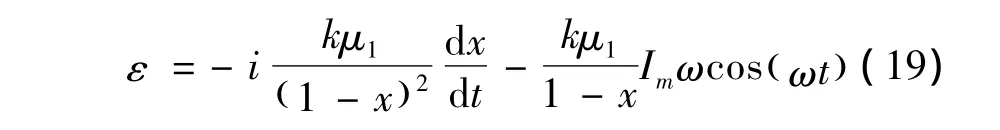
式(21)中s表示小球相对于传感器测量头的线位移，如图3所示。

图3 小球线位移示意图

由于环形球栅上的小球是重复出现的，式(21)便是整个环形球栅传感器在交流激励下输出信号的数学模型。式(21)中包含2部分信号，均是幅度调制信号，并且是以环形球栅的线位移为变量的函数;2部分信号的叠加构成了最后的输出信号，根据输出的信号便可确定对应的线位移。

3 基于环形球栅的扭矩测量模型

依据扭矩测量的机械原理，在主轴上安置2个传感器，一个靠近驱动部分，一个靠近负载，如图4所示。传感器固定在主轴上，传动轴转动时传感器与传动轴同步转动。2个传感器的激励信号是相同的。在主轴工作前，传动轴没有发生扭转变形，根据信号输出确定2路传感信号的初始线位移，进而确定初始线位移差值;传动轴开始工作后，发生扭转变形，2个传感器的位置绕传动轴发生相对转动，根据传感器输出同样可以确定工作线位移差值。

图4 扭矩测量示意图

当传动轴工作时，其线位移差值与初始线位移差值之差Δs与扭转角Δφ存在如下几何关系:

式中r为球心到轴线的距离，也就是球栅圆环的半径。根据式(21)可确定各传感器测取的线位移，代入式(22)便可确定机械传动轴的实时扭转角。

这种间接测量方法可以很好地测量较小的扭转角，减小了线位移的测量误差对测量结果的影响，提高了整个系统的测量精度，增强了整个系统的抗干扰能力。

4 环形球栅扭矩传感器结构设计

由于磁路通路不是由单一的介质构成，在磁介质相接处存在漏磁现象，这使得互感系数变小，感应线圈的输出信号较弱，容易混在噪声信号中不易于分离。通常采取单纯增大励磁铁芯大小或增加线圈匝数的方法，但是考虑到工程中的一些实际情况，可能同时带来信号饱和失真或增大传感器体积，或者引起局部电磁环境突变，造成同一工作环境中的其他部件不能正常工作。

解决这个问题可以通过结构上的改进来实现。测量头部分如图5所示，激励线圈位于铁芯中部使得铁芯内部磁场对称分布，在两臂上加上感应线圈，2个线圈串联在一起，以增强输出信号。

图5 测量头结构

在传感器结构部分，将4个测量头对称分布在球栅圆环上，对称的测量头为一组，感应线圈串接在一起，其空间结构如图6所示。

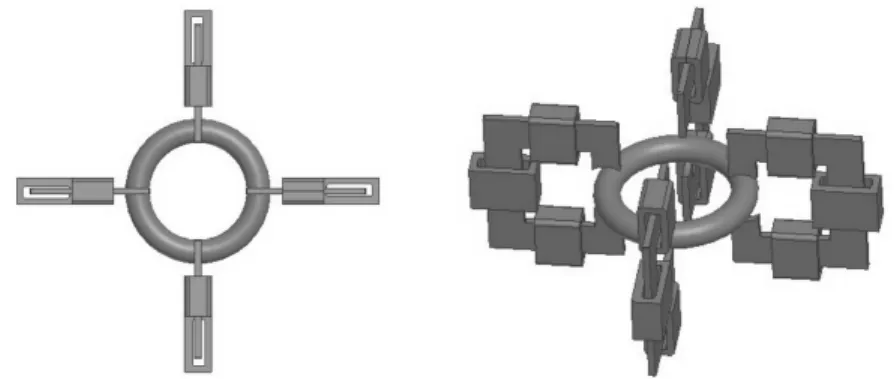
图6 测量头对称分布结构

原来环形球栅中的小球相互接触，在交流激励下将会使4个测量头相互影响。本研究对环形球栅进行了改进，使小球之间有一定的间距，且这个间距为铁芯的厚度，消除了可能引起的误差，同时保证了测量的连续性。改进后的环形球栅如图7所示。

图7 改进后的环形球栅

通过结构上的改进，可以达到增大输出信号、增强测量可靠性的目的。测量头的空间对称分布增强了传感器的抗干扰能力，同时避免了饱和失真和局部电磁环境突变。

5 环形球栅扭矩传感器仿真分析

使用Ansoft Maxwell电磁有限元仿真分析软件对设计的交流激励下的测量头对称传感器模型进行分析。由于测量头对称传感器整体结构的对称性，只需选择一路测量头进行分析即可［11］，简化后的模型如图8所示。

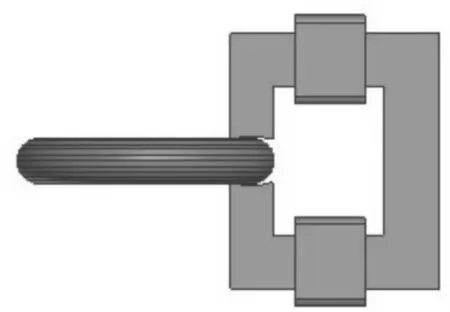
图8 仿真模型

激励线圈的匝数为100，每匝线圈激励电流为1 A，感应线圈匝数也为100，初始电压为零。为验证理论模型中感应输出信号是受小球的线位移调制的幅度调制信号，仿真了小球转动到不同位置时感应线圈的输出电压。激励线圈电流波形如图9所示，横坐标为时间，单位ms，纵坐标为激励电流值，单位为A。小球在原点时的输出电压波形与小球转动3°、6°后的输出电压波形分别如图10～12所示，横坐标为时间，单位ms，纵坐标为感应电压值，单位为mV。

从图10～12可看出:稳定后的输出电压波形呈正弦规律变化，具有与激励信号相同的周期，但是幅值却依次递减，很好地验证了理论模型的理论预测——感应输出信号是受小球线位移调制的幅度调制信号。

图9 激励线圈电流波形

图10 小球在原点时的感应电压波形

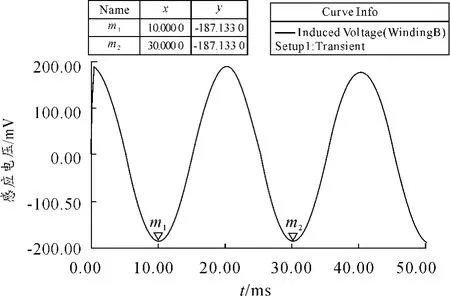
图11 小球转动3°时的感应电压波形

图12 小球转动6°时的感应电压波形

6 结束语

根据环形球栅的特点和电磁感应理论，建立了传感器理论模型，说明了传感器的工作原理，证明了该传感器理论上的可行性。结合扭矩的机械概念与传感器理论模型，建立了传感器与机械传动轴的基本结构关系，并在该传感器模型下得出了对机械传动轴扭矩的测量方法。针对非接触式电磁结构互感系数小的缺点，进行了针对性的结构改进，采用对称均匀分布测量头结构，同时通过将测量头输出线圈串联在一起，很好地增强了输出信号，减小了局部环境对传感器输出信号的影响，避免了单一测量激励信号大、尺寸大、对局部电磁环境影响大的弱点，使得交流激励下的测量头对称分布环形球栅扭矩传感器能满足机械传动轴动态、静态的测量需求，具有更好的环境适应性。最后，用电磁仿真分析软件Ansoft Maxwell对交流激励下的传感器模型进行了仿真分析，证明了该传感器原理的正确性，为后续的持续研究提供了参考依据。

［1］Salach J，Bienkowski A，Szewczyk R.The ring-shaped magnetoelastic torque sensors utilizing soft amorphous magnetic materials［J］.Journal of Magnetism and Magnetic Materials，2007，316：607-609.

［2］Garshelis I J，Kari R J，Tollens S P L.A rate of chang of torque senor［J］.IEEE Transactions on Magnetics，2007，43(6)：2388-2390.

［3］Chang M C，Mohri K.Improved pulse carrier MI effect by flash anneal of amorphous wires and FM wireless CMOS IC torque sensor［J］.IEEE Transactions on Magnetics，2001，37(4)：2038-2041.

［4］王登泉，杨明，叶林，等.非接触式旋转轴扭矩测量现状［J］.电子测量技术，2010，33(6)：8-12.

［5］谢平，刘彬，王霄，等.新型光纤扭矩测量方法［J］.光电工程，2006，33(2)：111-114.

［6］喻洪麟，巴军，何安国.环形空间阵列扭矩传感器设计及电磁分析［J］.仪器仪表学报，2009，30(8)：1687-1691.

［7］吴麒麟，喻洪麟.基于环形球栅的多电磁检测器原理［J］.重庆理工大学学报：自然科学版，2012，26(6)：89-94.

［8］陈天富，冯贤桂.材料力学［M］.修订版.重庆：重庆大学出版社，2006.

［9］物理学［M］.4版.北京：高等教育出版社，1999.

［10］邹继斌.磁路与磁场［M］.哈尔滨：哈尔滨工业大学出版社，1998.

［11］赵博，张洪亮.Ansoft 12在工程电磁场中的应用［M］.北京：中国水利电力出版社，2010.