电力系统外部等值网络快速修正方法

刘志文，刘明波，夏文波

（1.中国能源建设集团广东省电力设计研究院，广州 510663；2.华南理工大学电力学院，广州 510640）

电力系统外部等值网络快速修正方法

刘志文1，2，刘明波2，夏文波1

（1.中国能源建设集团广东省电力设计研究院，广州 510663；2.华南理工大学电力学院，广州 510640）

在基于外部静态等值的电力系统最优潮流计算中，为了保持外部等值精度，不断重新计算外部等值导纳矩阵将导致优化计算时间效率下降，文中针对Ward外部等值方法的特点，从不同解决思路入手，分别采用矩阵求逆辅助定理和支路等值注入功率模型提高外部等值网络参数修正计算速度，对两种快速修正方法的修正原理和计算过程做了充分的分析和说明，以IEEE 39节点系统和某538节点系统作为试验系统，验证所提方法的有效性，并对两种修正方法进行详细分析比较。

外部静态等值；Ward等值；矩阵求逆辅助定理；支路等值注入功率模型；参数修正

随着电力需求的日益增加，电力系统规模不断增大，电力数据采集量急速膨胀，使常规电力系统最优潮流计算暴露出诸多问题，如主机内存不足、计算速度慢、网络通信阻塞等弊病，难以满足在线分析和实时控制的要求[1-6]。通过采用外部等值方法简化分区外部网络，不仅能有效缩小问题规模，较好地解决大规模电网实时计算的难题，而且也与电力系统调度运行管理模式一致，因此基于外部等值方法的分解协调思想较多地应用到电力系统最优潮流和分布式潮流计算领域[7-13]。

在基于外部等值的分区最优潮流迭代计算过程中，各分区的外部系统中变压器变比将不断发生变化，由于外部等值属于静态等值，外部等值网络参数不会跟随外部系统的变动进行自动修正，为了确保外部等值的精确，必须重新计算外部等值导纳矩阵。对于大规模电力系统而言，若每次变动都重新计算外部系统等值导纳矩阵，需要不断对大规模矩阵进行求逆计算，这势必将会大大降低优化迭代计算的时间效益，从而抵消外部等值化简带来的计算速度优势。为了提高整体优化迭代计算速度，许多采用外部等值化简的电力系统最优潮流算法往往采用固定外部等值导纳矩阵的处理方式，如文献[12]和[13]只在初始时计算外部等值导纳值，而在优化过程中不再更新计算外部等值导纳，这样虽然提高了优化计算时间效益，但随着优化迭代计算进行，外部系统变压器变比不断变化，导致外部等值将不再不准确，从而对全网优化的收敛性和优化结果的准确性产生不良影响。因此需要寻找有效的大规模电力系统外部等值网络快速修正方法，在确保外部等值导纳矩阵精度的前提下，尽可能提高外部等值矩阵修正计算的速度。

本文在分析常用外部等值方法特点的基础上，从不同解决思路入手，分别采用矩阵求逆辅助定理和支路等值注入功率模型提高大规模电力系统外部等值网络修正计算速度，通过选用不同测试系统进行仿真，对这两种修正方法的适应范围和时间计算特性进行了详细的分析与比较。

1 外部等值方法

在电力系统分析计算中，Ward等值是最为常用的外部等值方法，这种外部等值是通过对电力网络进行星网变换而获得[14-15]。如图1（a）所示，电力系统网络按照区域划分可分为内部网络I、边界网络B和外部网络E。

图1（a）中的系统内部网络、边界网络和外部网络所对应的网络方程如下：

2 降低计算效益的主因与解决思路

图1 Ward等值网络化简过程Fig.1Network reduction process of Ward equivalent

3 基于矩阵求逆辅助定理的修正方法

3.1 矩阵求逆辅助定理

根据第一种解决思路，本文采用矩阵求逆辅助定理[15]减少对外部网络中导纳增量求逆所带来的计算量，该定理描述如下：

假设有n×n阶的非奇异矩阵A出现如式（9）所示的增量变化：

若式（10）中A-1已经计算出来，则对新矩阵的求逆只需在A-1基础上进行修正即可，假如矩阵a的阶次相对于A的阶次较低，则式（10）中右边括号中项的阶次也会比较低，那么采用式（10）求~A的逆将会十分迅速[15]。

3.2 采用矩阵求逆辅助定理求解

4 基于支路等值注入功率模型的修正方法

4.1 支路等值注入功率模型

变压器是电力系统的主要设备之一，在电力系统最优潮流计算过程中，需要通过不断地调节变压器变比才能获得最优解，图2所示为变压器支路的理想模型。

图2 变压器理想模型Fig.2Transformer ideal model

图2所示变压器模型中，kt为变压器变比值，yt是变压器支路导纳值。图3所示为图2中变压器模型对应的π型等值电路。

图3 变压器π型等值电路示意图Fig.3π-type equivalent circuit of transformer

图3中，S˙ij和S˙ji分别表示节点i和节点j处的等值注入功率，假若将图3中节点i与节点j之间的变压器等值导纳消去，则可获得如图4所示的变压器支路等值注入功率模型[17-18]。

对于图3所示的π型等值电路，基本潮流状态下，若设：

图4 变压器支路等值注入功率模型Fig.4Branch power injection model of transformer

由式（17）～（19）即可形成如图4所示通用的支路等值注入功率/电流模型。

4.2 外部网络变换与等值修正

通过采用支路等值注入功率模型，将外部网络中变压器变比发生变动的支路消去，并在对应支路的两端节点处分别添加等值注入功率或等值注入电流，这样外部网络的拓扑结构将发生变化，变换之前的外部网络节点导纳矩阵YEE与变换之后的节点导纳矩阵Y′EE将不再相等。如图2所示，假设外部网络中的节点i和节点j之间的变压器变比出现变动，且节点i是非标准变比侧，Yii和Yjj分别对应变换前节点i和j的自导纳，采用支路等值注入功率对外部网络变压器支路进行变换后，则与节点i和节点j相对应的导纳元素[16]为

5 算例分析

5.1 测试系统

本文以IEEE 39节点系统和某538实际系统作为测试系统，对本文所提的两种快速修正方法进行有效性验证。其中IEEE 39节点系统分为2个区域，其分区情况如图5所示。

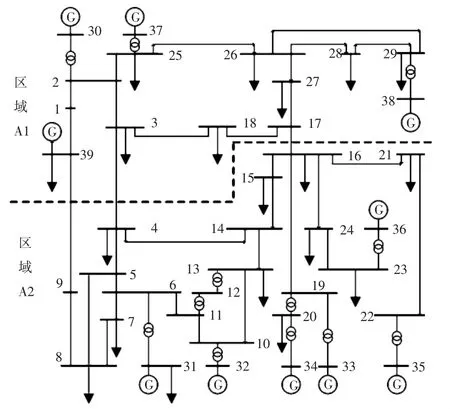
图5 IEEE 39节点系统2分区示意图Fig.5Schematic diagram of 2 areas in IEEE 39-bus system

图5中虚线以上部分为区域A1，在仿真过程中作为内部系统，虚线以下部分为区域A2，在仿真过程中作为外部系统并进行Ward等值化简，两分区的基本信息如表1所示。

表1 IEEE 39节点系统2分区基本数据Tab.1Basic data of two areas in IEEE 39-bus system

538节点实际系统包括538节点、593条线路、48台发电机、98台电容器组和409台变压器支路（其中64台参与优化计算）。将该系统划分为A1和A2两个区域，如图6所示。

图6538 节点系统2分区示意图Fig.6Schematic diagram of 2 areas in 538-bus system

在图6所示的2个分区域中，区域A2规模较大，在仿真过程中以A2作为外部系统进行Ward等值化简，两个分区基本信息如表2所示。

表2 538节点系统2分区基本信息Tab.2Basic data of 2 areas in 538-bus system

5.2 计算结果分析

本文采用Matlab7.1仿真平台，在计算机配置为Pentium（R）4（2.8 GHz），512 MB内存环境下对上述两个测试系统的外部Ward等值网络进行修正计算，仿真结果如表3所示。

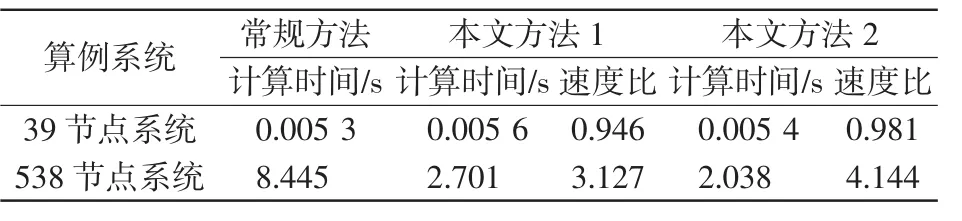
表3 三种外部等值网络修正方法计算结果比较Tab.3Comparison results obtained from three kinds of external equivalent correction method

表3中常规方法是指直接重新计算外部等值网络的方法。本文方法1是指采用矩阵求逆辅助定理的外部等值网络快速修正方法，本文方法2是指基于支路等值注入功率模型的外部等值网络快速修正方法。计算时间是外部系统中所有变压器变比在可调范围内同时随机变化10次，并且在每次外部系统变比变化后都进行外部等值修正计算，将这10次修正计算时间累加的总和。速度比是指常规方法计算时间与本文方法1或本文方法2的计算时间的比值。

由表3可知，39节点系统采用常规方法修正外部等值网络的时间很少，几乎可以忽略不计，而538节点系统采用常规方法的计算时间已比较可观，为39节点系统计算时间的1593倍，这说明当外部系统规模小时，外部等值网络修正计算量很小，但随着外部系统规模的增大，修正求逆的计算量呈几何级数增长，导致外部等值网络的计算时间激增。表3中39节点系统采用本文方法1和本文方法2进行外部等值修正计算时间比常规方法计算时间还长一点，本文方法1和本文方法2的与常规方法的速度比分别为0.946和0.981，而538节点系统分别采用本文所提两种方法后，外部等值修正速度得到大幅度提高，速度比分别达到3.127和4.144，其主要原因是对小规模的外部系统而言，外部等值修正计算量本来就很少，额外的技术处理还需要占据一定的计算量，这使得本文采用的两种方法的速度优势不明显，甚至更慢。而对大规模外部系统而言，额外的技术处理所占修正计算量比重很小，加速优势更为明显，因此能大幅度地提高计算速度。

从表中横向比较来看，对于大小不同的两个测试系统，本文方法2的计算速度均高于本文方法1的计算速度，主要原因是本文方法1采用矩阵求逆辅助定理后仍然需要进行一定的矩阵求逆计算，且求逆的规模与外部系统变压器支路数量密切有关。而本文方法2在经过外部网络变换后不需要每次都进行求逆计算，因此计算速度更快一些。由两种修正方法的计算原理可知，本文方法1和2从外网等值导纳矩阵计算角度来说都属于精确修正，但方法2是将外网变压器变比变动的影响等效地转移到等值节点注入功率中去，这样处理对基于外网等值的最优潮流计算误差的影响还需要进一步研究。此外，就应用性而言，采用矩阵求逆辅助定理需要的外部信息较少，也更容易处理和实现，且没有将外部系统变压器变比变动的影响转化为边界等值注入功率，其应用的适用性更广。

6 结论

（1）采用矩阵求逆辅助定理的外部等值网络修正方法是根据外部网络发生扰动时节点导纳矩阵变动的特点，将增量矩阵进行分解后运用矩阵求逆辅助定理实现快速求逆，从而提高外部等值网络的修正计算速度。

（2）基于支路等值注入功率模型的外部等值修正方法通过采用支路等值注入功率替换外部网络中变压器支路，将外部变压器变比变动的影响转移到边界等值注入功率上去，从而避免重新计算外部等值导纳矩阵。

（3）仿真表明采用矩阵求逆辅助定理和支路等值注入功率模型的外部等值网络修正方法都能大幅度提高大规模外部等值网络修正计算速度，并且基于支路等值注入功率模型的修正方法的计算速度高于采用矩阵求逆辅助定理的修正方法，但对小规模外部等值网络的修正计算速度优势均不明显。

[1]Deeb N，Shahidehpour S M．Linear reactive power optimization in a large power network using the decomposition approach[J]．IEEE Trans on Power Systems，1990，5（2）：428-438．

[2]Wang X，Song Y H，Lu Q．Lagrangian decomposition approach to active power congestion management across interconnected regions[J]．IEE Proceedings-Generation，Transmission and Distribution，2001，148（5）：497-503．

[3]李运华，吴宏昺，盛万兴，等（Li Yunhua，Wu Hongbing，Sheng Wanxing，et al）．分布式并行混合遗传算法在无功优化中的应用（Application of distributed parallel hybrid genetic algorithm in reactive power optimization）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（2）：36-41．

[4]Nogales F J，Prieto F J，Conejo A J．A decomposition methodology applied to the multi-area optimal power flow problem[J]．Annals of Operations Research，2003，120（1-4）：99-116．

[5]李钟煦，刘玉田（Li Zhongxu，Liu Yutian）．一种地区电网分布式无功优化方法（Distributed reactive power optimization for area power system）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（2）：80-83．

[6]刘科研，盛万兴，李运华（Liu Keyan，Sheng Wanxing，Li Yunhua）．基于分布式最优潮流算法的跨区输电阻塞管理研究（Multi-region transmission congestion management based on distributed optimal power flow algorithm）[J]．中国电机工程学报（Proceedings of the CSEE），2007，27（19）：56-61．

[7]Hao Shangyou，Papalexopoulos A.External network modeling for optimal power flow applications[J].IEEE Trans on Power Systems，1995，10（2）：825-837．

[8]Tognete A L，Nepomuceno L，dos Santos A.Framework for analysis and representation of external systems for online reactive-optimisation studies[J].IEE Proceedings-Generation，TransmissionandDistribution，2005，152（6）：755-762．

[9]Tognete A L，Nepomuceno L，dos Santos A.Evaluation of economic impact of external equivalent models used in reactive OPF studies for interconnected systems[J].IET Generation，Transmission and Distribution，2007，1（1）：140-145．

[10]张海波，张伯明，孙宏斌（Zhang Haibo，Zhang Boming，Sun Hongbin）．基于异步迭代的多区域互联系统动态潮流分解协调计算（A decomposition and cooperation dynamic power flow calculation for multi-area interconnected system based on asynchronous iteration）[J]．电力系统自动化（Automation of Electric Power Systems），2003，27（24）：1-5，9.

[11]朱永兴，张步涵（Zhu Yongxing，Zhang Buhan）．电力系统潮流分解协调并行计算（Decomposition and coordination power flow parallel calculation）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22 （5）：97-101．

[12]赵维兴（Zhao Weixing）．大型互联电力系统无功优化分解协调算法研究（Research on Decomposition and Coordination Algorithm of Reactive Power Optimization for Large in Connected Power Systems）[D]．广州：华南理工大学电力学院（Guangzhou：School of Electric Power of South China University of Technology），2008．

[13]赵维兴，刘明波，孙斌（Zhao Weixing，Liu Mingbo，Sun Bin）．基于诺顿等值的多区域系统无功优化分解协调算法（A Norton equivalence based decomposition and coordination algorithm ofreactive power optimization for multi-regional power grid）[J]．电网技术（Power System Technology），2009，33（11）：44-48，54．

[14]夏道止．电力系统分析（下册）[M]．北京：中国电力出版社，1995．

[15]张伯明，陈寿孙．高等电力网络分析[M]．北京：清华大学出版社，1996．

[16]刘志文，刘明波（Liu Zhiwen，Liu Mingbo）．基于支路等值注入功率模型的外部网络等值修正方法（A corrected external equivalent approach using branch equivalent injection power model）[J]．电力系统保护与控制（Power System Protection and Control），2010，38（21）：219-226．

[17]Wei Yan，Juan Yu，Yu D C，et al.A new optimal reactive power flow model in rectangular form and its solution by predictor corrector primal dual interior point method[J]. IEEE Trans on Power Systems，2006，21（1）：61-67．

[18]Jabr R A，Coonick A H，Cory B J．A primal-dual interior point method for optimal power flow dispatching[J]．IEEE Trans on Power Systems，2002，17（3）：654-662．

Fast Correction Approaches of External Equivalent Network in Power Systems

LIU Zhi-wen1，2，LIU Ming-bo2，Xia Wen-bo1
（1.Guangdong Electric Power Design Institute，China Energy Engineering Group Co.，Ltd.，Guangzhou 510663，China；2.School of Electric Power，South China University of Technology，Guangzhou 510640，China）

During the optimal power flow calculation of power system based on external static equivalent，in order to maintain the accuracy of external equivalent，the equivalent admittance matrices of external networks is recalculated，which reduces the efficiency of optimal computational time.According to the characteristics of Ward external equivalent，this paper uses inverse matrix modification lemma and branch equivalent injection power model to improve the calculation speed of external equivalent parameter correction，and the external equivalent correction principles and calculation processes of the two kinds of correction methods are analyzed and introduced in depth.Furthermore，the IEEE 39-bus systems and a 538-bus practical system are used as the test systems to validate the effectiveness of the proposed correction methods，and the comparisons between these two kinds of external equivalent correction methods are given in detail.

external static equivalent；Ward equivalent；inverse matrix modification lemma；branch equivalent injection power model；parameter correction

TM862

A

1003-8930（2013）04-0044-07

刘志文（1980—），男，博士后，工程师，研究方向为电力系统优化、运行与控制。Email：lzw32347@126.com

2012-03-15；

2012-07-02

国家自然科学基金项目（50777021）；广东省绿色能源技术重点实验室资助项目（2008A060301002）

刘明波（1964—），男，博士，教授，博士生导师，研究方向为电力系统优化、运行与控制。Email：mingboliu@scut.edu.cn

夏文波（1968—），男，硕士，教授级高级工程师，研究方向为电力系统通信与调度自动化。Email：wenboxia@gedi.com.cn