考虑单位购电成本变动的风电场出力偏差约束

李泓泽，王宝，郭森，苏晨博

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学电气与电子工程学院，北京 102206）

考虑单位购电成本变动的风电场出力偏差约束

李泓泽1，王宝1，郭森1，苏晨博2

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学电气与电子工程学院，北京 102206）

为将风电场出力存在偏差时电网公司单位购电成本变化量控制在可接受的范围内，有必要确定其最大变动范围。本文通过构建含风电场的优化调度模型，并借助于原对偶内点算法对其求解，定量识别了风电场出力存在偏差时电网公司单位购电成本变化量及其主要影响因素，进而基于回归分析方法测度了风电场出力偏差幅度的最大变动范围。算例结果验证了该方法的合理性和有效性。

风电场；原对偶内点算法；单位购电成本；偏差幅度

风能资源的大力开发和利用，并取代部分常规机组发电量，不仅可以节省电力系统运行的燃料消耗，而且降低了碳排放，能够很好地服务于节能减排目标。然而风电场出力受地区风速影响，具有较强的随机性。大量风电场并网发电可能会影响甚至危及系统稳定运行，因而风电场出力或地区风速预测的准确性会对调度部门的调度难易程度及系统稳定性产生较大的影响。

文献[1-3]提出了利用小波分析、神经网络、支持向量机以及卡尔曼滤波等方法的风电场输出功率预测模型。文献[4-6]提出了采用神经网络、时间序列分析、灰色理论以及混沌加权零阶局域方法的风电场风速预测模型。含风电场的电力系统，受政策引导，调度部门优先全额调度风电场出力，并对常规发电机组经济调度[7]。文献[8-10]研究了含风电场电力系统动态经济调度问题。风电场的出力预测往往存在一定的误差，这就需要调度部门按照经济调度调整各常规发电机组出力水平以保证系统的稳定运行，结果会改变电网公司购电成本，从而存在着一定的单位购电成本变化量。

1 风电优先调度下电网公司单位购电成本的计算

1.1 含风电场的优化调度模型及电网公司单位购电成本的计算

对于含风电场的电力系统，尽管风电环境效益优良，但其单位发电成本明显高于常规发电机组，在经济调度下风电场出力将不能被很好地利用，目前我国实施优先调度风电的政策。

假定某电力系统含n个常规发电机组CPP （conventional power plant）和m个风电场WF（wind farm），某日前竞价交易的一个交易时段内，负荷需求为PD，各风电场预测出力为PWF（jj=1，2，…，m），系统运营部门优先调度风电出力后对常规发电机组实行经济调度，以从常规发电机组购电成本最小为目标函数，等式约束为系统有功功率平衡约束，且省略了功率传输损耗PLoss，不等式约束包括各CPP机组有功出力上下限约束。

式中：PCPPi表示常规发电机组i的调度出力；PCPPimax和PCPPimin分别表示常规发电机组i的出力上下限；aCPPi、bCPPi和cCPPi为常规发电机组i的成本特性参数。

1.2 经济调度优化模型求解

CPP机组的经济调度优化模型是一个典型的带约束的非线性规划问题，本文借助于原对偶内点算法[11]加以求解，该方法实际上是通过引入松弛变量将不等式约束转化为等式约束，在使用拉格朗日乘子将等式约束和不等式约束与目标函数一起构建无约束拉格朗日函数，并用牛顿法对其一阶最优性条件进行迭代寻优。

首先引入松弛向量l和u将式（1）中的不等式约束转化为等式约束，设f（PCPP）和g（PCPP）分别表示目标函数和有功功率平衡等式约束，PCPP表示CPP机组出力列向量。构造无约束拉格朗日函数L。

式中：λ、z和w为拉格朗日乘子，μ为障碍因子，且μ〉0，μ=σGap（/4n），对偶间隙Gap=lTz+uTw，中心参数σ∈（0，1）。

式（4）的一阶Karush-Kuhn-Tucker（KKT）条件为

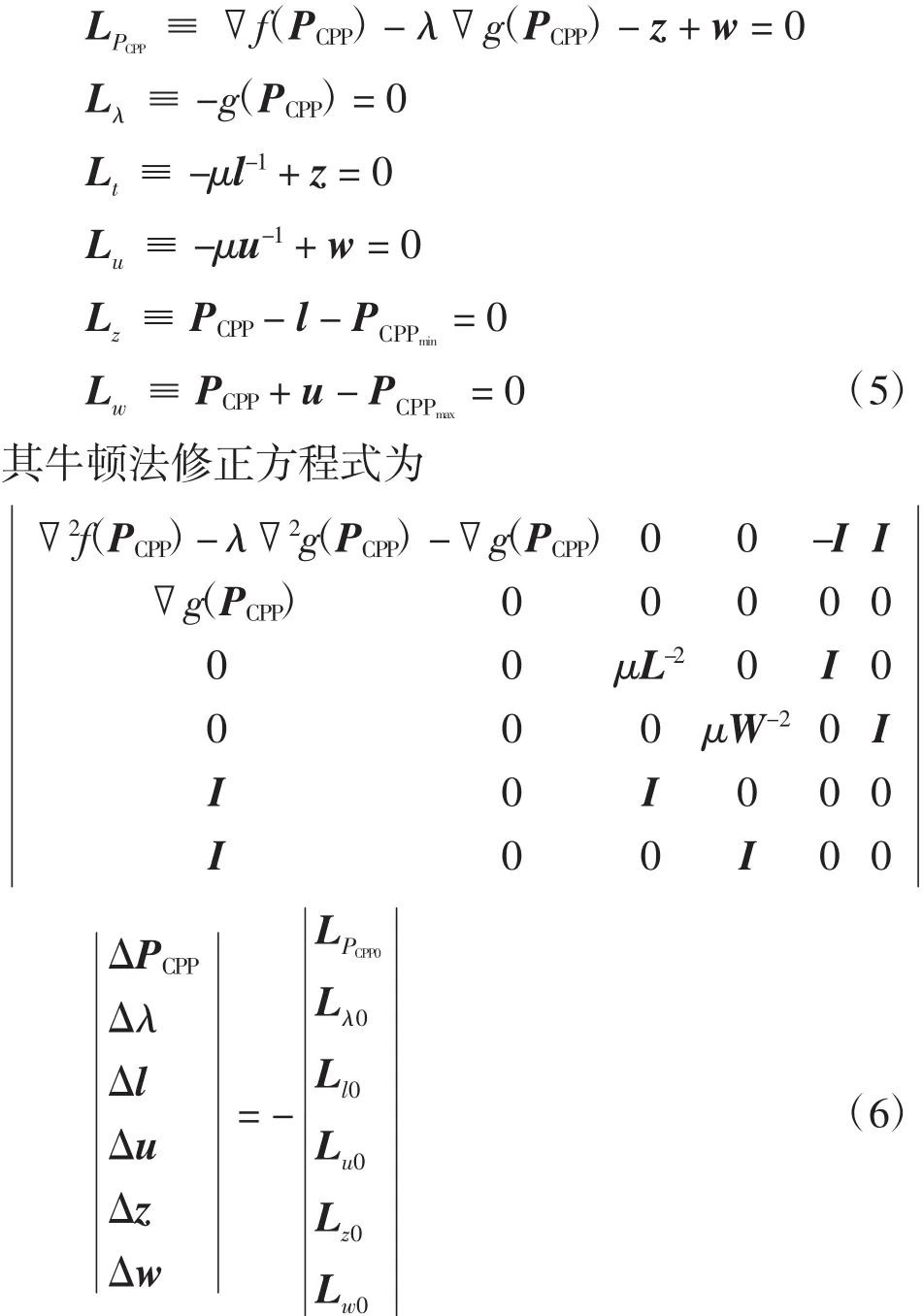
式中l-1和u-1表示l和u各元素的倒数，L-2和W-2表示l-1和u-1对应元素的平方组成的对角矩阵，I为单位矩阵。原对偶内点算法的计算核心在于每次迭代过程的牛顿法修正方程式的形成及求解上。

于是得到原对偶内点算法的迭代过程如下。

（6）转入第2步，并置k=k+1，若k〉kmax，停止迭代，输出最优解。

2 风电场出力偏差下电网公司单位购电成本变化量的识别

日前竞价交易的各交易时段内均根据风电场提交的出力预测值，优先全额收购风电场出力，在风电场实际出力与提交的预测出力一致时，电网公司单位购电成本UC可通过式（2）计算得到。但风电场出力预测值较实际值往往会有一定的偏差，调度部门需要对调度计划进行一定的修正，调整常规发电机组的出力水平，以使系统稳定运行。从而改变了机组出力的调度计划，这往往影响到电网公司的购电成本。

设各风电场出力偏差幅度为δj（j=1，…，m），在风电优先调度下，调度部门需要根据经济调度调整CPP机组出力水平，于是得到风电场出力偏差下电网公司单位购电成本UC′为

3 风电场出力偏差对电网公司单位购电成本的影响及其变动范围分析

由式（11）可以看出，风电场出力偏差下电网公司单位购电成本变化量ΔUC与风电场出力偏差幅度、机组成本特性、CPP机组原始调度出力、CPP机组调度出力调整量以及交易时段内负荷需求有关。CPP机组原始调度出力主要受交易时段内负荷需求、CPP机组成本特性以及风电场出力直接影响，因而在CPP和WF机组成本特性给定的情况下，各CPP机组原始调度出力受各风电场出力预测值和负荷需求PD影响。而各CPP机组出力调整量受、δj和PD影响。从而得出：风电场出力偏差下电网公司单位购电成本变化量主要受风电场预测出力、出力偏差幅度和负荷需求直接决定。

风电场出力可能存在正偏差和负偏差，当出现正偏差后，调度部门需要优先调度风电场的实际出力，因而需要适当降低CPP机组的出力以维持系统稳定，由于风电场发电成本较CPP机组高，因而电网公司单位购电成本变化量为正；当出现负偏差后，风电场实际出力未能达到申报的水平，调度部门需要增加CPP机组的出力以维持系统稳定，低发电成本的常规机组替代了高成本的部分风电场出力，从而电网公司单位购电成本变化量为负。

理论上，在风电场预测出力和负荷需求保持不变的情况下，某风电场出力正、负偏差幅度越大，|ΔUC|就越大；在出力偏差幅度和负荷需求保持不变的情况下，某风电场预测出力越大，|ΔUC|就越大；在风电场预测出力和出力偏差保持不变的情况下，负荷需求越大，|ΔUC|就越小。

为了保证电力系统的稳定运行，风电场出力预测的偏差幅度不应过大，那么对于任意WF，电网公司单位购电成本变化量就应该存在着一个可接受的最大量，设为|ΔUC|max。考虑到不同预测出力以及负荷需求下，风电场出力预测偏差幅度对电网公司单位购电成本变化量的影响不尽相同，存在不同出力预测值的风电场在不同负荷需求下应该存在着不同的δj上下限和，以满足|ΔUC|max的要求，即

于是可以确定不同负荷需求下不同出力预测值的风电场出力偏差幅度的最大可接受范围[，]，超出此幅度范围的风电场需要支付一定的惩罚金，从而既可以鼓励风电场厂商提高出力预测的准确性，又不失合理性。

4 算例分析

含7个CPP机组和3个WF的电力系统为例，某日前竞价交易的某个交易时段（长度为15 min）内系统总负荷需求PD=240 MW，各机组相关参数如表1。各WF提交调度部门的预测出力分别为4 MW、2.5 MW和8 MW。并且对于每个WF，设电网公司单位购电成本变化量的最大可接受量|ΔUC|max= 0.2元/（kW·h）。

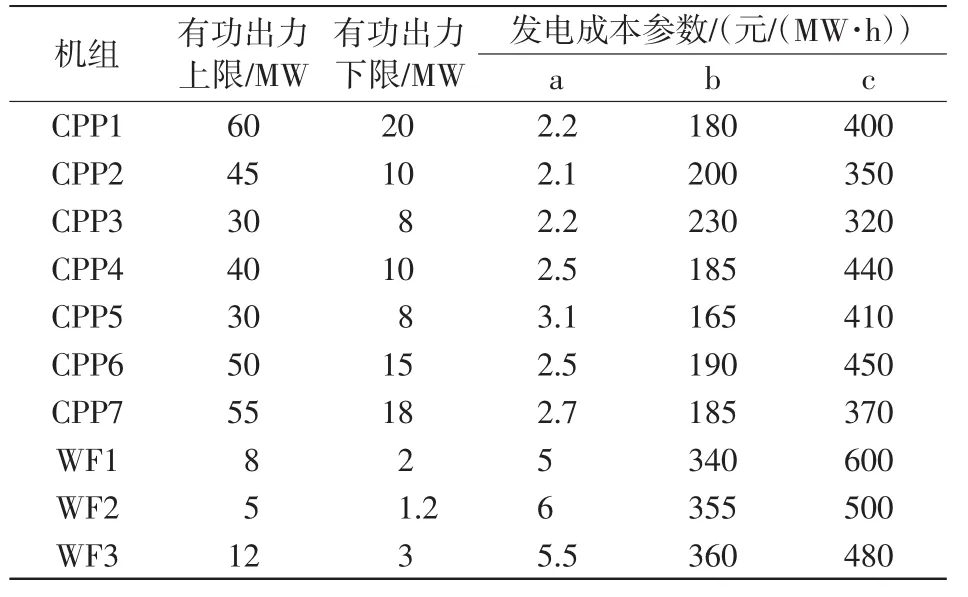
表1 各发电机组相关参数Tab.1Related parameters of each generator

调用编写的原对偶内点算法程序，得到原始调度计划：各WF出力水平分别为4 MW、2.5 MW 和8 MW，各CPP机组出力分别为38.397 MW、35.463 MW、27.033 MW、32.789 MW、29.669 MW、31.789 MW和30.36 MW，电网公司购电成本为17670元，单位购电成本为294.5元/（MW·h）。

本算例在分析WF出力存在偏差对电网公司单位购电成本影响的过程中，对3个WF分别讨论在其他两个WF出力无偏差而只有其中1个WF出力存在偏差的情况下，其不同的偏差幅度对电网公司单位购电成本变化量的影响，并把其出力偏差最大允许幅度限定在[-20%，20%]范围内。图1给出了不同δ对应的电网公司单位购电成本变化量情况。电网公司单位购电成本变化量随WF出力偏差幅度的增加而增加，且正负偏差幅度所引致的单位购电成本变化量并不对称，正偏差引起的变化量明显高于负偏差引起的变化量。相同偏差幅度下，风电场预测出力越大，引起的单位购电成本变化量越大，WF3的出力预测值为WF1的2倍，但由WF3出力偏差引起的单位购电成本变化量平均为WF1的7.8倍。

图1 不同δ对应的电网公司单位购电成本变化量Fig.1Change in Grid Company′s power purchase unit cost corresponding to different δ

图2给出了WF1和WF3出力无偏差的情况下，WF2不同出力预测值下各δ对应的电网公司单位购电成本变化量情况。随着WF2预测出力的增加，相同偏差幅度引致的单位购电成本变化量也增加，且增速加快。WF2预测出力为3.5 MW时的变化量是2.5 MW时的平均2.03倍，WF2预测出力为4.5 MW时的变化量是2.5 MW时的平均3.42倍。因而，预测出力大的风电场，其允许的出力偏差上下限应较小，以保证系统的稳定运行。

图2 WF2不同出力预测值下各δ对应的电网公司单位购电成本变化量Fig.2Change in Grid Company′s power purchase unit cost corresponding to different δ under different WF2′s forecast outputs

图3给出了WF1和WF2出力无偏差时，不同负荷需求下WF3的各δ对应的电网公司单位购电成本变化量情况。随着负荷需求的增加，相同偏差幅度引致的单位购电成本变化量不断下降。系统负荷为220 MW时的变化量是180 MW时的平均0.66倍，系统负荷为260 MW时的变化量是180 MW时的平均0.41倍。因而，低谷时段风电场允许的出力预测偏差幅度上下限较高峰时段低。

进一步可以确定WF2和WF3出力无偏差且系统负荷不变的情况下，WF1不同预测出力值下的各偏差幅度对应的单位购电成本变化量的偏导数∂ΔUC/∂δ1。图4给出了WF1三种不同预测出力下的单位购电成本变化量对δ1的偏导数，即为敏感性系数。如当WF1预测出力为6 MW时，偏差幅度在δ1=5%时的偏导数为1.166 7，表明：若偏差幅度再增加0.1%，电网公司单位购电成本将增加0.001 166 7元/（MW·h）。敏感性系数随着正偏差幅度的增加而增大，随负偏差的增大而减小，并呈现直线的趋势。基于回归分析，可确定不同出力预测值下的偏导数方程，当WF1出力为8 MW时，单位购电成本变化量对δ1的偏导数方程为

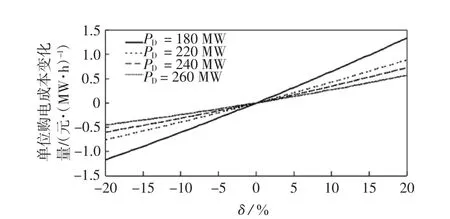
图3 WF3在不同负荷需求下各δ对应的电网公司单位购电成本变化量Fig.3Change in Grid Company′s power purchase unit cost corresponding to different δ of WF3 under different load demands

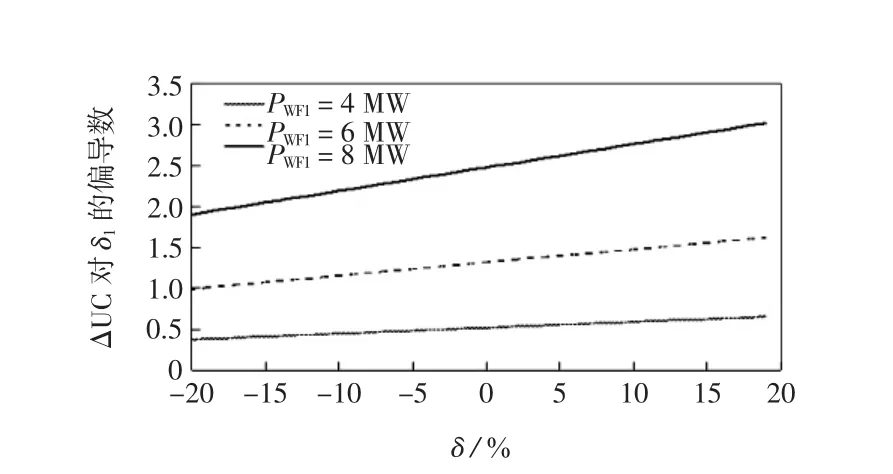
图4 WF1不同预测出力下各δ对应的电网公司单位购电成本变化量的偏导数Fig.4Partial derivative of change in Grid Company′s power purchase unit cost corresponding to different δ of WF1 under different load demands

可得到系统负荷为240 MW、WF1预测出力为8 MW时的偏差幅度上下限，分别为7.73%和-8.5%，即此交易时段内若WF1预测出力为8 MW时其出力偏差幅度不能超过[-8.5%，7.73%]的范围，否则单位购电成本将超出可接受的上限。

同理，可求得其他两个WF出力无偏差情况下，不同负荷需求和预测出力下的某一WF对应的电网公司单位购电成本变化量关于出力偏差幅度的二次方程式，进而求得其可接受偏差幅度上下限。

表2给出了系统负荷需求分别为240 MW和260 MW时，各WF不同出力预测值对应的可接受偏差幅度上下限。各WF出力偏差幅度上下限主要受负荷需求和预测出力的影响，负荷需求越大，允许的偏差幅度范围越大，WF预测出力越大，允许的偏差幅度范围越小。

表2 两种负荷需求下不同预测出力的各WF对应的偏差幅度上下限Tab.2Upper and lower limits of each WF′s deviation range in two load demands and different forecast outputs context

5 结语

本文定量识别了含风电场的电力系统，在风电场出力存在偏差情况下，电网公司单位购电成本的变化量，进而探讨了该变化量的主要影响因素。基于回归分析方法定量测度了不同负荷需求下不同出力预测值对应的风电场出力偏差幅度的最大变动范围。市场运营部门可通过相应的奖惩机制来激励各并网风电场提高预测精度，以将其出力偏差对电网公司单位购电成本的影响控制在可接受的范围以内。本文为市场运营部门在单位购电成本变化量的识别以及风电场出力偏差幅度的最大变动范围的确定上提供了一定的参考价值。

[1]王丽婕，冬雷，廖晓钟，等（Wang Lijie，Dong Lei，Liao Xiaozhong，et al）.基于小波分析的风电场短期发电功率预测（Short-term power prediction of a wind farm based on wavelet analysis）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（28）：30-33.

[2]刘纯，范高锋，王伟胜，等（Liu Chun，Fan Gaofeng，Wang Weisheng，et al）.风电场输出功率的组合预测模型（A combination forecasting model for wind farm output power）[J].电网技术（Power System Technology），2009，33 （13）：74-79.

[3]李智，韩学山，韩力，等（Li Zhi，Han Xueshan，Han Li，et al）.地区电网风电场功率超短期预测方法（An ultrashort-term wind power forecasting method in regional grids）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（7）：90-94.

[4]戴浪，黄守道，黄科元，等（Dai Lang，Huang Shoudao，Huang Keyuan，et al）.风电场风速的神经网络组合预测模型（Combination forecasting model based on neural networks for wind speed in wind farm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（4）：27-31.

[5]张国强，张伯明（Zhang Guoqiang，Zhang Boming）.基于组合预测的风电场风速及风电机功率预测（Wind speed and wind turbine output forecast based on combination method）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（18）：92-95，109.

[6]罗海洋，刘天琪，李兴源（Luo Haiyang，Liu Tianqi，Li Xingyuan）.风电场短期风速的混沌预测方法（Chaotic forecasting method of short-term wind speed in wind farm）[J].电网技术（Power System Technology），2009，33 （9）：67-71.

[7]栾士岩，蒋传文，张焰，等（Luan Shiyan，Jiang Chuanwen，Zhang Yan，et al）.含风电场的电力系统节能减排优化调度研究（Research on optimization dispatching for saving energy and reducing emissions in wind power integrated power system）[J].华东电力（East China Electric Power），2010，38（1）：39-43.

[8]陈海焱，陈金富，段献忠（Chen Haiyan，Chen Jinfu，Duan Xianzhong）.含风电场电力系统经济调度的模糊建模及优化算法（Fuzzy modeling and optimization algorithm on dynamic economic dispatch in wind power integrated system）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（2）：22-26.

[9]周玮，彭昱，孙辉，等（Zhou Wei，Peng Yu，Sun Hui，et al）.含风电场的电力系统动态经济调度（Dynamic economic dispatch in wind power integrated system）[J].中国电机工程学报（Proceedings of the CSEE），2009，29 （25）：13-18.

[10]姜文，严正（Jiang Wen，Yan Zheng）.基于一种改进粒子群算法的含风电场电力系统动态经济调度（Dynamic economic dispatch considering wind power penetration based on IPSO）[J].电力系统保护与控制（Power System Protection and Control），2010，38（21）：173-178，183.

[11]郭靖，陈青，张卫星（Guo Jing，Chen Qing，Zhang Weixing）.电力系统无功优化的原对偶内点算法及其应用（Primal-dual interior point algorithm for reactive power optimization）[J].电力自动化设备（Electric Power Automation Equipment），2004，24（5）：41-43.

Constraint of Wind Farm′s Output Deviation Considering Change in Power Purchase Unit Cost

LI Hong-ze1，WANG Bao1，GUO Sen1，SU Chen-bo2
（1.School of Economics and Management，North China Electric Power University，Beijing 102206，China；2.School of Electrical and Electronic Engineering，North China Electric Power University，Beijing 102206，China）

According to the output deviation of wind farm，it is necessary to determine its maximum change range to constrain the change in Grid Company′s power purchase unit cost within the acceptable range.This paper quantitatively identifies the change in Grid Company′s power purchase unit cost as well as its main influencing factors when wind farm has output deviation by establishing an optimal dispatching model with wind farm considered and applying the primal-dual interior point algorithm to its solving.Subsequently，the maximum change range of wind farm′s output deviation is measured on the basis of regression analysis.The results of test example demonstrate the rationality and validity of the proposed method.

wind farm；primal-dual interior point algorithm；power purchase unit cost；deviation range

TM73

A

1003-8930（2013）04-0073-06

李泓泽（1970—），男，硕士，副教授，硕士生导师，研究方向为电力市场经济分析、电力经济管理等。Email：lihongze@ 163.com

2011-10-24；

2011-11-14

北京市哲学社会科学规划项目资助（11JGB070）

王宝（1986—），男，硕士研究生，研究方向为电力市场经济分析。Email：kevinwong1010tg@163.com

郭森（1987—），男，硕士研究生，研究方向为工业技术经济分析。Email：guosen324@163.com