计及风电的发电系统可靠性评估

蒋程，刘文霞，于雷，王昕伟，刘先正，刘军

（1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.华锐风电科技（集团）股份有限公司，北京 102206；3.中国电力科学研究院，北京 100192）

计及风电的发电系统可靠性评估

蒋程1，刘文霞1，于雷1，王昕伟1，刘先正2，刘军3

（1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.华锐风电科技（集团）股份有限公司，北京 102206；3.中国电力科学研究院，北京 100192）

考虑风速和负荷预测误差的随机性、风力发电机组和常规机组的停运率，应用蒙特卡洛仿真方法对含风电场的发电系统进行可靠性评估。针对发电系统概率抽样中蒙特卡洛算法样本容量大、效率低等不足，提出了分散抽样蒙特卡洛算法，此抽样算法将[0，1]区间分成若干子区间，在抽样后分别对每个子区间进行系统状态判断和指标计算，从而增加故障状态的抽样频率，提高抽样效率，在满足精度要求下，有效地减少了抽样次数。以含10台常规机组和1个风电场的发电系统进行了仿真，结果验证了该评估方法的有效性。

蒙特卡洛仿真；可靠性评估；发电系统；分散抽样；风电场

电力系统可靠性是指电网在各种运行条件下，向用户持续提供符合一定质量要求电能的能力[1]。风力发电对发电系统的影响主要是因为风电的间歇性和随机性[2-3]。电力系统在正常运行情况下，系统能够正常供电，不会出现切负荷的事件。如果系统受到某些偶发事件的扰动，特别是风电并网后风电的间歇性和波动性，可能会引起系统功率失衡、线路过载和节点电压超限等故障，进而导致切负荷[4]。发电-负荷需求系统常常被称为发电系统，对其进行可靠性评估所关注的是发电设施的充裕性，并称之为第一层次的研究，同时也是基础研究[5]。

对发电系统进行可靠性评估，首先要建立系统主要元件的可靠性模型，文献[6-8]考虑了风能的随机性、风电机组的老化和故障等环节，用两状态马尔可夫过程建立风电机组的可靠性模型，但其模型中只包含停运和运行两状态，此方法在传统发电机组的可靠性建模中是可行的；但风力发电机组处在降额状态的时间在整个运行期间所占比例较大[9]，忽略其降额状态将带来较大误差。

蒙特卡洛方法是一种统计试验法，其原理简单、易于实现，适合大规模发电系统的可靠性分析[10]。但由于蒙特卡洛方法需要的样本容量与系统的规模成指数关系增长，而且其抽样次数与计算精度的平方成正比，这就意味着为了得到较高的精度往往需要大量的抽样样本和更多的抽样时间[11-13]。文献[14-16]分别提出提高蒙特卡洛抽样的抽样效率和收敛速度，但在应用中都存在一些制约。

针对上述问题，本文首先结合常规机组的3状态可靠性模型，考虑风电机组的降额运行状态，建立了风电机组3状态可靠性模型；其次针对蒙特卡洛方法中样本容量大、计算效率低等不足，提出了分散抽样方法，其原理是把[0，1]区间分成若干子区间，在抽样后分别对每个子区间进行系统状态的判断和指标计算，从而提高了样本中失效状态的抽样次数，有效地减小了样本方差，提高了蒙特卡洛方法的效率。

1 风力发电机组模型

1.1 风速预测模型

风速预测对风电场和电力系统的运行都具有重要意义，可有效减轻或避免风电场对电力系统的不利影响。但因风能的随机性很强，一般风速预测误差在25%～40%[17]。为表征风速预测误差的随机性，通常认为其服从标准正态分布[18]，如：

风速实际值可表示为

式中：vwind表示风速的实际值；μwind表示风速预测的均值；σwind表示风速预测标准差。

1.2 风力发电机组的出力

根据空气动力学原理，风力发电机组发出的电功率跟风速的3次方成正比[19]，其输出功率与风速的关系可表示为

式中：vci代表切入风速；vco代表切出风速；vr代表额定风速；PWR代表额定风速下风机发出的有功功率；V为该风场的风速值；PW（V）代表风速V下风机发出的有功功率。

1.3 风力发电机组停运模型

包含运行、降额和停运状态的三状态模型如图1所示。

图1 风力发电机组三状态模型Fig.1Three-state model for wind power generator

图中，λw（停运次数/年）和λwd（降额次数/年）分别为停运和降额状态的转移率；μw（停运修复次数/年）和μwd（降额修复次数/年）分别为从停运和降额状态修复的修复率。

通常情况下认为发电机的停运和降额状态是随机事件，将马尔可夫方法[20]应用于图1所示的状态空间图，可得出以下结果：

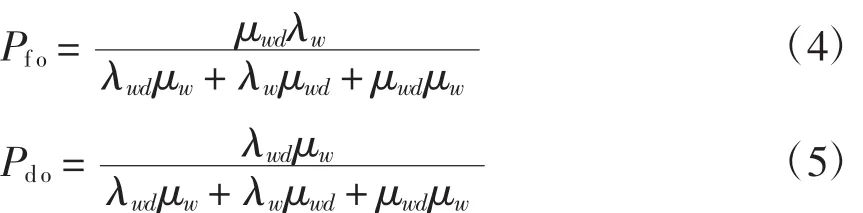
式中，Pfo和Pdo分别为停运和降额状态的概率。

2 发电机和负荷模型

2.1 发电机的停运模型

发电机的强迫停运可以通过稳态“运行-停运-运行”的循环过程来模拟，长期循环过程中的平均不可用率可表示为[20-21]：

式中，PfoT为机组停运的概率。

2.2 负荷模型

发电系统风险评估必须计及负荷曲线，由于负荷预测具有随机性和不确定性，通常用正态分布来表征负荷预测结果[22-23]，第i级负荷可表示为

式中：PiL表示负荷的实际值；μi表示负荷均值；σi2表示标准差；下标i表示负荷的级数。

3 分散抽样蒙特卡洛方法

3.1 常规蒙特卡洛方法

蒙特卡洛方法一般也被称为状态抽样法，被广泛用于电力系统风险评估中，其基本原理是：每个元件的状态可以由该状态出现的概率确定，所有元件状态的组合构成整个系统的状态。

对于系统中任一个元件m，设其停运率为λm，对于某次抽样得到的[0，1]区间的随机数Rm，元件的状态可表示为

根据式（8），对系统中所有元件进行抽样确定其状态，则包含M个元件的系统抽样状态可表示为

当系统状态在抽样中被选定后，可对系统进行分析和判断，若为失效状态，则对该状态的可靠性指标函数进行估计和计算。

当抽样的数量足够大时，系统状态S的抽样频率可作为其概率的无偏估计，如式（10）所示。

式中∶NS为抽样次数；n（S）为状态S出现次数。

当每个系统状态概率通过抽样估计出来后，便可计算系统可靠性指标的均值，表达式为

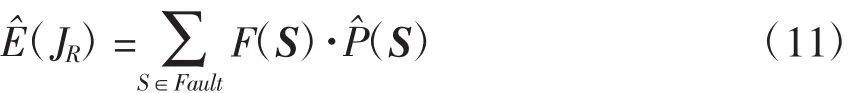
式中：JR为可靠性指标的实际值；F（S）为状态S的后果函数；）代表状态S出现的概率。

用式（11）估计可靠性指标的不确定性可用样本均值的方差进行量度，其定义为

蒙特卡洛模拟达到的精度水平可用方差系数来量度，其可表示为

3.2 分散抽样蒙特卡洛方法

由式（13）可以看出，用蒙特卡洛抽样法计算出来的可靠性指标的精度与抽样样本的方差成正比，因此减小样本方差就可减小抽样误差，从而提高抽样精度。

分散抽样方法是通过减小样本方差的办法来提高蒙特卡洛抽样的效率，其具体思路如下所述。

把[0，1]区间分成H个等长度子区间，且满足：

式中：λ为元件的停运率；下标M代表系统中元件的个数。

式中：Sh代表第h个子区间内元件的状态；H表示子区间数；Um表示随机抽样值；λm表示元件的停运率；Sm表示元件在整个区间的状态。

对应第h个子区间，定义系统的后果函数为F（Sm），对于整个区间，系统后果函数可表示为

式中，F（Sm）代表整个区间内系统的后果函数。

4 基于分散抽样法的发电系统可靠性评估

4.1 风力发电机组状态抽样

根据式（4）和式（5）可求出风力发电机组的停运率和降额率，在[0，1]区间抽取均匀分布的随机数Uwind，根据蒙特卡洛抽样的原理，可得风力发电机在每次抽样的状态为

式中：Swind代表发电机组的状态；Pfo代表发电机组停运状态的概率；Pdo为降额状态的概率。

4.2 常规发电机组状态抽样

根据式（6）可以求出常规机组的停运率，在[0，1]区间抽取均匀分布的随机数，则常规发电机在每次抽样时的状态为

式中：ST代表发电机组的状态；PfoT代表发电机组停运的概率。

4.3 风速和负荷概率抽样

一般情况下可以采用逆函数法[19]确定服从一定分布随机变量的抽样值，但由于正态累积概率分布函数的逆函数不存在解析表达式，可使用下面的近似表达式来计算风速和负荷的抽样值[22]。

标准正态分布下的随机变量为

式中：X为标准正态分布下的随机变量；U为[0，1]区间分布的随机数；ci和di为变换参数。

对于风力发电机组，设其抽样值为Uwind，则对应的风速为

式中：vwind表示风速的实际值；μwind表示风速预测的均值；σwind表示风速预测标准差。

对于常规机组，设其抽样值为UT，则其对应的负荷可表示为

式中：PL表示负荷的实际值；μT表示负荷均值；σT表示标准差。

4.4 发电系统可靠性评估

在发电系统可靠性指标体系中主要以切负荷指标度量系统的可靠性，其中充裕性指标包括缺电时间概率LOLP（loss of load probability）、期望停电功率EPNS（expected power not supplied）、期望停电电量EENS（expected electric not supplied）等，本文重点计算指标LOLP和EPNS。

缺电时间概率LOLP在指给定时间区间内系统不能满足负荷需求的概率，即：

式中：Pi表示系统处于状态的概率；S表示给定时间区间内不能满足负荷需求的系统状态的全集。

期望停电功率EPNS指系统在给定时间区间内因发电容量短缺造成负荷需求削减的期望值，即：

式中：Pi表示系统处于状态i的概率；Fi是在状态i下削减的负荷功率；S是给定时间区间内造成系统负荷削减的状态全集；期望缺供电力用MW表示。

为了提高蒙特卡洛方法的抽样效率，把[0，1]区间等分成H个子区间，每个区间的长度为1/H，对于第h个子区间，抽样得到的发电系统状态可定义为

其中：Sh表示第k次抽样下系统的状态；Gh表示在第h个区间中抽样所得的总发电容量；Lh表示在第h个区间中抽样所得的总负荷量。

对于每次抽样，系统缺电概率可表示为

式中：Prk表示第k次抽样系统缺电概率；Sk表示第k次抽样系统的状态。

当抽样次数足够多时，缺电概率可以用样本均值来近似表示，把式（26）代入式（23），整理可得：

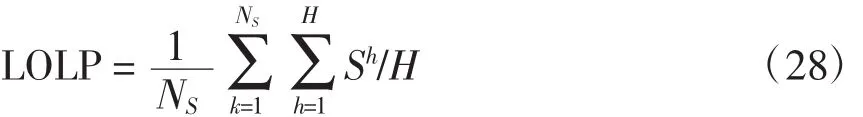
对于第h个子区间，抽样得到的发电系统的电力削减可表示为

式中：Fk表示在第k次抽样中发电系统电力不足的后果；Fh表示第h个子区间内电力不足的后果；Lh和Gh分别表示第h个区间中抽样所得的总负荷量和总发电量。

期望缺供电力可用样本中所有切负荷的均值表示，把式（27）和式（30）代入式（24），整理得：

发电系统可靠性评估的流程如图2所示，可靠性评估的基本步骤为：

1）输入电力系统原始数据：包括火电机组停运率；风电机组停运率和降额率，风速和负荷预测均值和方差；最大采样次数及最小方差系数。

2）随机抽样：在[0，1]区间内随机抽取M+N个随机数，根据式（18）和式（19）判断发电机组的状态；抽取2个随机数，分别根据式（21）和式（22）计算风电场的风速和系统的负荷。

3）根据式（26）判断发电系统的状态，并根据式（28）和式（31）计算可靠性指标。

4）根据式（13）计算方差系数，若满足精度要求，则采样结束，否则检查采样次数，若达到最大值，则采样结束，否则，令

转入步骤2）。

5）输出电力可靠性指标。

图2 可靠性评估流程图Fig.2Flow chart of reliability assessment

5 算例分析

5.1 算例描述

采用10机系统进行计算分析[15-17]，该系统含有10台燃煤机组和1个风电场组成，其中风电场由200台1.5 MW的风电机组组成。燃煤机组和风电机组的参数分别如表1和表2所示。考虑风速和负荷预测的随机性和不确定性，用两参数正态分布来模拟风速和负荷，某时刻风速和负荷预测的参数如表3所示。

5.2 评估结果分析

在MATLAB中编写了10机系统的可靠性指标计算程序，其中采样次数为50000，H=3，指标LOLP和EPNS的计算结果如表4所示。

表1 燃煤机组参数Tab.1Parameters of the thermal generators

表2 风电机组参数Tab.2Parameters of the wind turbines

表3 风速和负荷的参数Tab.3Parameters of wind speed and load

表4 10机系统的可靠性指标Tab.4Reliability index of 10 machines system

从表4可看出，采用分散抽样蒙特卡洛法对系统进行可靠性评估能够满足精度要求。

5.3 收敛速度仿真

为了比较两种方法的收敛速度，蒙特卡洛法和分散抽样蒙特卡洛法的抽样次数都设为50 000次，LOLP和EPNS的仿真结果如图3～6所示。

图3 指标LOLP的收敛过程Fig.3Convergence process of Index LOLP

图3为指标LOLP的收敛过程，图4为LOLP的计算精度，图5为指标EPNS的收敛过程，图6 为EPNS的计算精度。从中可以看出采用分散抽样蒙特卡洛法，系统的可靠性指标收敛速度明显高于蒙特卡洛法，而且在相同抽样次数下前者的计算精度也高于后者。

5.4 抽样效率仿真

为了验证分散抽样蒙特卡洛法具有较高的抽样效率，对于相同的计算精度0.01，需要的抽样次数如表5所示。

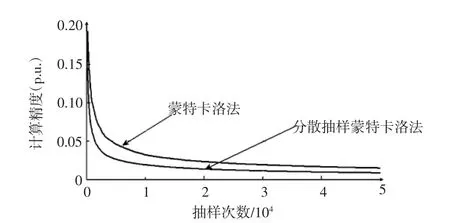
图4 指标LOLP的计算精度Fig.4Calculation precision of Index LOLP

图5 指标EPNS的收敛过程Fig.5Convergence process of Index EPNS

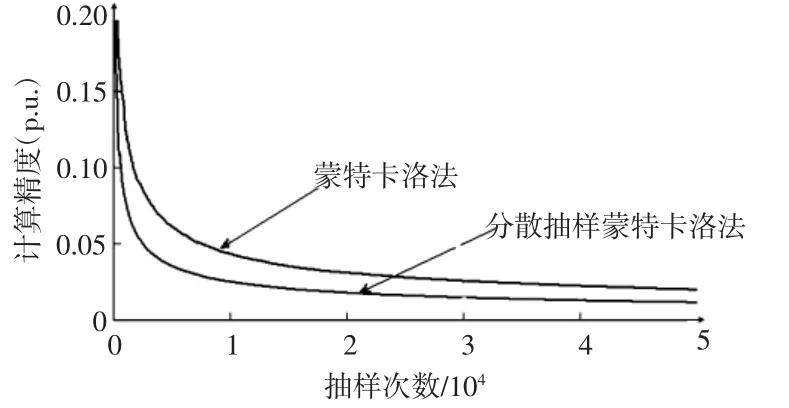
图6 指标EPNS的计算精度Fig.6Calculation precision of Index EPNS

表5 相同计算精度下抽样次数Tab.5Sampling times in the same calculation precision

从表5中可看出，对于相同的计算精度，分散抽样蒙特卡洛法比蒙特卡洛法需要较少的抽样次数，从而前者比后者具有较高的抽样效率；可靠性指标EPNS比LOLP收敛得慢，在相同精度下，指标EPNS需要更多的抽样次数。

5.5 不同子区间个数仿真

为了研究不同分区数H对可靠性指标的影响，H分别取3、4、5，抽样次数均为30 000次，系统可靠性指标的计算结果如表6所示。

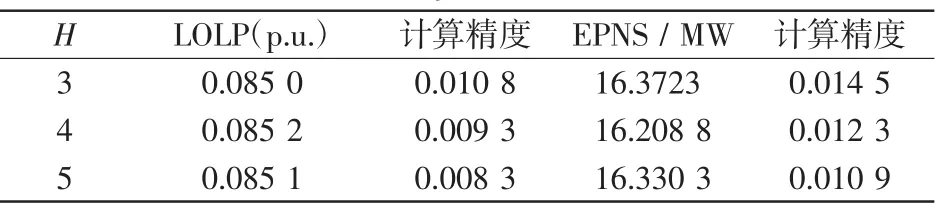
表6 不同H下系统的可靠性指标Tab.6Reliability index in different H

从表6可看出，在相同抽样次数下，随着H增加系统的可靠性指标更精确，其计算精度更高。

6 结论

通过对含1个风电场的10机发电系统进行分仿真分析，得到如下结论：1）在计算可靠性指标时，基于分散抽样的蒙特卡洛法与蒙特卡洛法相比具有更快收敛速度；2）对于相同的抽样次数时，分散蒙特卡洛法比蒙特卡洛法具有更高计算精度；发动系统的可靠性指标LOLP比指标EPNS收敛的快；3）分散抽样蒙特卡洛法中H取不同的值，对可靠性指标有较大的影响，主要表现在：随着分区数量增加，即H的增大，可靠性指标的计算精度提高。

[1]郭永基.电力系统可靠性分析[M].北京：清华大学出版社，2003.

[2]Ummels Bart C，Gibescu Madeleine，Pelgrum Engbert，et al．Impacts of wind power on thermal generation unit commitment and dispatch[J]．IEEE Trans on Energy Conversion，2007，22（1）：44-51．

[3]周明，冉瑞江，李庚银，等（Zhou Ming，Ran Ruijiang，Li Gengyin，et al）.风电并网系统可用输电能力的评估（Assessment on available transfer capability of wind farm incorporated system）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（22）：14-21.

[4]黄学良，刘志仁，祝瑞金，等（Huang Xueliang，Liu Zhiren，Zhu Ruijin，et al）.大容量变速恒频风电机组接入对电网运行的影响分析（Impact of power system integrated with large capacity of variable speed constant frequency wind turbines）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（4）：142-149.

[5]刘若溪，张建华，刘文霞，等（Liu Ruoxi，Zhang Jianhua，Liu Wenxia，et al）.发电系统运行风险的评估算法（Method of operational risk assessment for generating system）[J]．中国电机工程学报（Proceedings of the CSEE），2011，31（31）：134-141.

[6]李大字，冯园园，刘展，等（Li Dazi，Feng Yuanyuan，Liu Zhan，et al）．风力发电机组可靠性建模与维修策略优化（Reliability modeling and maintenance strategy optimization for wind power generation sets）[J]．电网技术（Power System Technology），2011，35（9）：122-127.

[7]吴义纯，丁明（Wu Yichun，Ding Ming）．基于蒙特卡罗仿真的风力发电系统可靠性评价（Reliability assessment of wind power generation system based on Monte-Carlo simulation）[J]．电力自动化设备（Electric Power Automation Equipment），2004，24（12）：70-73.

[8]Bowden G J，Barker P R，Shestopal V O，et al．The Weibull distribution function and wind power statistics[J]. Wind Engineering，1983，7（2）：85-98.

[9]杨明明（Yang Mingming）.大型风电机组故障模式统计分析及故障诊断（Fault Mode Statistic&Analysis and Failure Diagnosis of Large-scale Wind Turbines）[D].北京：华北电力大学电气与电子工程学院（Beijing：College of Electrical&Electronic Engineering of North China Electric Power University），2009.

[10]段玉兵，龚宇雷，谭兴国，等（Duan Yubing，Gong Yulei，Tan Xingguo，et al）．基于蒙特卡罗模拟的微电网随机潮流计算方法（Probabilistic power flow calculation in microgrid based on Monte-Carlo simulation）[J]．电工技术学报（Transactions of China Electrotechnical Society），2011，26（S1）：274-278.

[11]吴变桃，肖登明（Wu Biantao，Xiao Dengming）．用改进的蒙特卡罗法模拟SF_6和CO_2混合气体电子崩参数（An improved Monte-Carlo method for simulation of electron swarm parameters of SF_6 and CO_2 gas mixtures）[J]．电工技术学报（Transactions of China Electrotechnical Society），2007，22（1）：13-16．

[12]黄殿勋，张文，郭萍，等（Huang Dianxun，Zhang Wen，Guo Ping，et al）．发输电系统可靠性评估的蒙特卡洛改进算法（The Monte-Carlo improved method for reliability evaluation of generation and transmission systems）[J]．电力系统保护与控制（Power System Protection and Control），2010，38（21）：179-183.

[13]宋宇，孙富春，李庆玲（Song Yu，Sun Fuchun，Li Qingling）．移动机器人的改进无迹粒子滤波蒙特卡罗定位算法（Mobile robot Monte-Carlo localization based on improved unscented particle filter）[J]．自动化学报（Acta Automatica Sinica），2010，36（6）：851-857．

[14]别朝红，王建华，王锡凡（Bie Chaohong，Wang Jianhua，Wang Xifan）．一种减小蒙特卡洛模拟方差的新方法（A new method for reducing Monte-Carlo simulation variants）[J]．中国电力（Electric Power），1999，32（12）：41-44．

[15]郑开逸，李臣贵，黄莉，等（Zheng Kaiyi，Li Chengui，Huang Li，et al）．蒙特卡罗模拟-重要抽样法评估三七含铅的健康风险（Assessment of the health risk of lead in Panax Notoginseng with Monte-Carlo simulation and important sampling）[J]．计算机与应用化学（Computers and Applied Chemistry），2010，27（5）：649-653．

[16]马俊海，杨非（Ma Junhai，Yang Fei）．可转换债券蒙特卡罗模拟定价的控制变量改进方法（Improved control variable methods of Monte-Carlo simulation for pricing convertible bonds）[J]．系统工程理论与实践（Systems Engineering-Theory&Practice），2009，29（6）：77-85．

[17]罗文，王莉娜（Luo Wen，Wang Lina）．风场短期风速预测研究（Short-Term wind speed forecasting for wind farm）[J]．电工技术学报（Transactions of China Electrotechnical Society），2011，26（7）：68-74．

[18]张国强，张伯明（Zhang Guoqiang，Zhang Boming）.考虑风电接入后二次备用需求的优化潮流算法（Optimal power flow approach considering secondary reserve demand with wind power integration）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（8）：25-28.

[19]Hetzer J，Yu D C，Bhattarai K．An economic dispatch model incorporating wind power[J].IEEE Trans on Energy Conversion，2008，23（2）：603-611．

[20]李文沅．电力系统风险评估-模型、方法和应用[M]．北京：科学出版社，2006.

[21]黄银华，彭建春，李常春，等（Huang Yinhua，Peng Jianchun，Li Changchun，et al）．马尔科夫理论在中长期负荷预测中的应用（Application of Markov theory in mid-long term load forecasting）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：131-136．

[22]王成山，柴华，谢小荣，等（Wang Chengshan，Chai Hua，Xie Xiaorong，et al）．综合负荷模型动静负荷比例的在线辨识（Online identification of percentage of dynamic component in composite load model）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（3）：14-19．

[23]赵希人，李大为，李国斌，等（Zhao Xiren，Li Dawei，Li Guobin，et al）．电力系统负荷预报误差的概率密度函数建模（Probability density function modeling for power system load forecasting errors）[J]．自动化学报（Acta Automatica Sinica），1993，19（5）：562-568．

Reliability Assessment of Power Generation System Considering Wind Power Penetration

JIANG Cheng1，LIU Wen-xia1，YU Lei1，WANG Xin-wei1，LIU Xian-zheng2，LIU Jun3
（1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources，North China Electric Power University，Beijing 102206，China；2.Sinovel Wind Group Co.，Ltd.，Beijing 102206，China；3.China Electric Power Research Institute，Beijing 100192，China）

The reliability of power generation system with Wind Power Penetration is evaluated based on Monte-Carlo simulation.In the reliability assessment，the prediction error randomness of wind speed and power load，failure rate of wind turbine generator and conventional generator are taken into account.Monte-Carlo simulation used in power generation system needs large sample size and has low efficiency.So the scattered sampling technique which divides the interval[0，1]into several sub-interval is applied to Monte-Carlo simulation.In each sub-interval，the system status need to be judged and indexed respectively.The scattered sampling technique is able to reduce sample times and enhance sampling efficiency.A simulation for power generation system with 10 conventional generators and 1 wind farm is carried out.The result verifies the adaptability and feasibility of the proposed evaluation strategy in generation system.

Monte-Carlo simulation；reliability assessment；power generation system；scattered sampling technique；wind farm

TM732

A

1003-8930（2013）04-0007-07

蒋程（1986—），男，博士研究生，研究方向为电力系统分析与控制、电力系统安全和可靠性分析。Email：jc_2002@ 163.com

2012-07-23；

2012-08-20

国家高技术研究发展计划（863计划）项目（2012AA050201）

刘文霞（1967—），女，博士，副教授，研究方向为电力系统自动化智能规划、电力系统通信等。Email：liuwenxia001@163. com

于雷（1976—），男，博士研究生，研究方向为电力系统分析与控制、电力系统安全和可靠性分析。Email：yulei@163. com