布莱克窗函数频域插值电力谐波计算

唐轶，陈奎，韩智强，陈雷，杨洛

（中国矿业大学信息与电气工程学院，徐州 221008）

布莱克窗函数频域插值电力谐波计算

唐轶，陈奎，韩智强，陈雷，杨洛

（中国矿业大学信息与电气工程学院，徐州 221008）

提出了一种电力谐波高精度估计的新方法。首先使用CZT（Chirp Z变换）从含有谐波的电力信号中高精度提取基波相量，并从中减去基波信号；然后加布莱克（Blackman）窗截断电力信号，用快速傅里叶变换（FFT）计算出剩余信号的频谱；再依据基波频率精确估计出各谐波的频率；最后依据各谐波频率对Blackman窗函数在频域插值，精确计算出各电力谐波的参数。仿真试验表明，该方法与加窗双谱线插值FFT分析电力谐波方法有基本同等的估值精度，但计算量约为1/2。

线性调频Z变换；快速傅里叶变换；谐波分析；布莱克窗；频域内插

电力电子技术的发展，非线性负荷在电力系统中的应用的增加，电力系统谐波污染日益严重，谐波已成为影响电能质量的主要问题[1]。快速傅里叶变换FFT（fast Fourier transform）是谐波分析最快捷的工具[2]。FFT精确分析频谱的前提是信号的同步采样和整周期截断，而实际电网频率通常在工频附近波动的，虽然从理论上说通过锁相环技术可解决同步采样和整周期截断问题[3，4]。电网频率并非恒定值，锁相环响应需要时间，因而难以保证完全同步采样。普遍采用的思路是通过选择谱能量主要集中在主瓣的窗函数，以减小谱间干扰[5～12]；通过双谱线间插值拟合修正，以减小栅栏效应，进而提高谐波估计精度[6～13]。加窗插值拟合法有效地提高了谐波估计的精度，但随着插值修正曲线拟合函数的阶次增高及谐波含有次数的增多，谐波估计精度提高的同时计算量大量增加。本文将提出谐波高精度估计的另一思路，直接对窗函数连续频谱内插精确计算谐波相量。

1 CZT简介

设x（n）为信号采样序列，其长度为N，n= 0，1，…，n，…N-1，其Z变换为

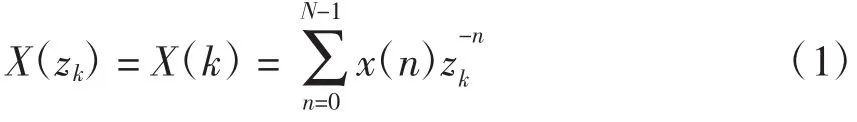
式中，zk为z平面抽样点，k=0，1，…，M-1。

如果沿z平面上一段螺线作等分角抽样，如图1所示，抽样点为

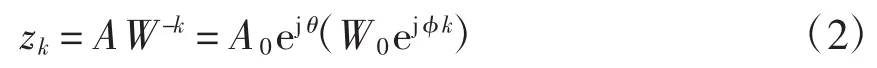
式中：A0是起始抽样半径；θ为起始抽样点的角频率；W0是螺线的伸展率，W0〉1向外延伸，W0〈1向内收缩；φ为相邻两抽样点之间的角频率差，φ〉0表示抽样路径逆时针旋转，φ〈0表示抽样路径顺时针旋转。

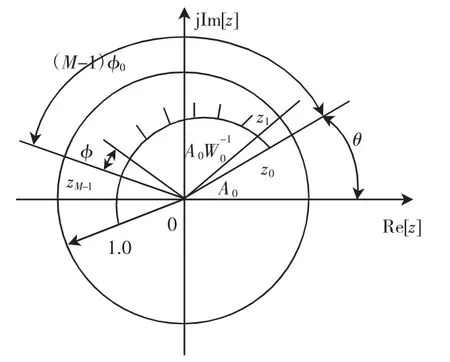
图1 CZT在z平面上的螺旋抽样Fig.1CZT screw slag sampling in z-plane

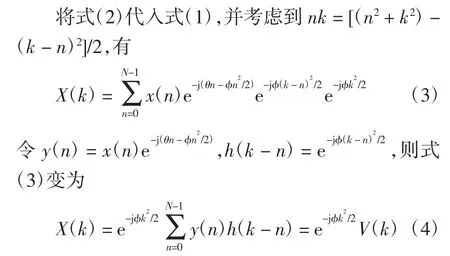
式中，V（k）=y（k）h（k）可以看成是一个数字网络的单位脉冲响应的输出，可用FFT快速求得：V（k）= IFFT[FFT[y（k）]FFT[h（k）]]。由于式（4）的单位脉冲响应h（n）的频率随时间成线性增加的线性调频信号相似，因此这种变换就称为线性调Z变换（Chirp-Z transform）或CZT[14]。

考察式（4）可见：其一，可以计算单位圆上任意一段线段上的频率样本，而且可以任意给定起始频率θ，终止频率θ+（M-1）φ；其二，频率样本的点数M可以任意给定，而频率抽样间隔φ随着M的增大而缩小，这一特点可达到细化频率、密集谱线、减小栅栏效应的目的。这两个特点显然具有精确地从含有谐波的电力信号中提取基波参数的优势。根据标准[15]，电网最大允许频率偏差为±0.5Hz，因此，可设待分析频段的起始频率为θ=2π×49.5，终止频率为θ+（M-1）φ=2π×50.5，即分析带宽为1 Hz。如果信号采样频率为fs=6 400 Hz，若取M=1 280（10个周波），则频率抽样间隔φ=2π/ 127 9=2π×7.818 61×10-4。若取模最大值所对应的频率作为基波频率估计值f1，频率测量的误差为|Δf|=（φ/2π）/2≤3.909 30×10-4Hz。因此，按图2计算流程可计算得基波信号的频谱X（k），进而分别计算得基波的幅值A1、频率f1和相位φ1分别为

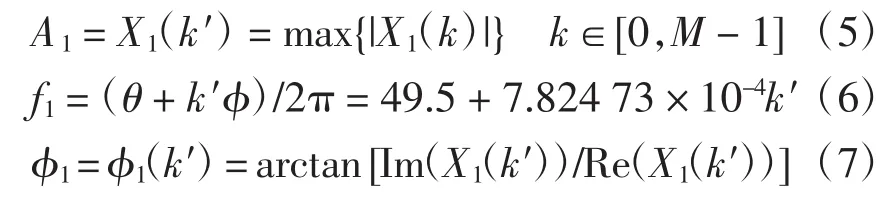
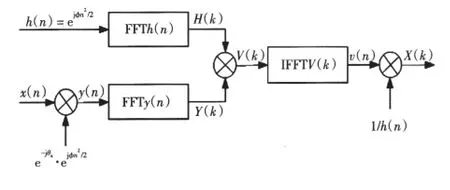
图2 快速CZT算法流程Fig.2Fast CZT algorithm process

2 窗函数频域插值谐波相量的计算

单频电力谐波信号为

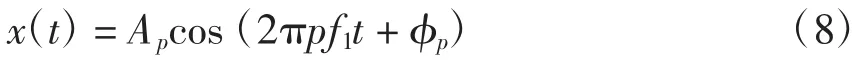
式中：p∈[0，P]，p为谐波次数，是正整数，P为最高谐波次数；Ap为第p次谐波幅值；f1为电力信号基波角频率；φp为第p次谐波初相角。

以采样频率fs=1/Ts对式（8）离散化，得数字序列为

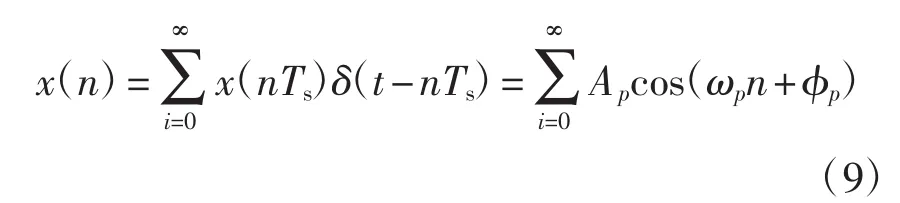
式中：Ts为采样周期；ωp=2πpf1Ts为p次谐波数字角频率。x（n）经Fourier变换后的连续频谱为

Blackman窗函数[13]为

可预定以电网的基波额定频率f1′=50 Hz的2i倍（i=1，2，…）采样，即采样频率fs=1/Ts=50× 2i。这样，电网基波和谐波的额定频率是与Blackman窗函数同步采样并能整周期截断的。则ωp′=2πpf1′Ts是p次电力谐波信号与Blackman窗函数同步采样并整周期截断的数字角频率，以角频率ωp′在Blackman窗函数连续频谱上在频域内抽样，必然有WBla（ωp-ωp′）=1，如图3所示（仅示出正频段）。

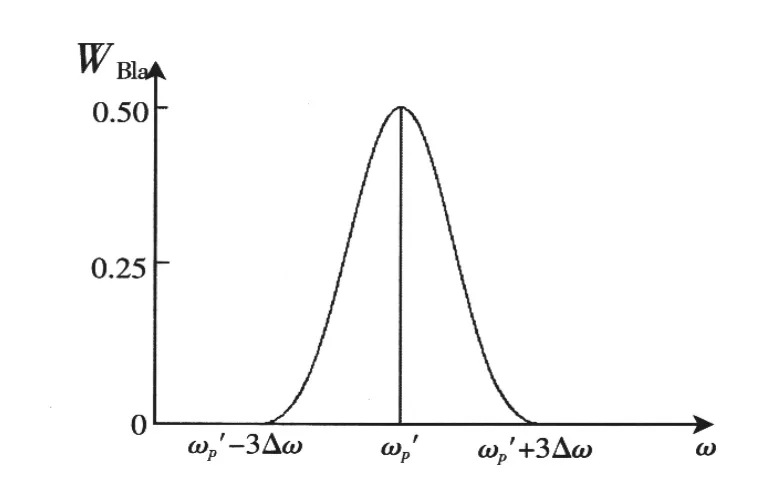
图3 同步采样和正周期截断后的频谱Fig.3Spectrum with synchronous sampling and integral period truncation

同时p次谐波信号的实际数字角频率ωp= 2πpf1Ts也在同一Blackman窗函数连续频谱上在频域内抽样求得WBla（ωp-ωp′），如图4所示（仅示出正频段）。

由此可求得p次电力谐波。

幅值校正系数为

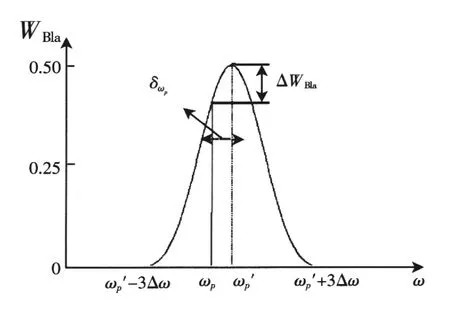
图4 非同步采样和非整周期截断后的频谱Fig.4Spectrum with nonsynch ronous sampling or non-integral period truncating

对xBla（n）的FFT实际上就是以Δω=2π/N等间隔对XBla（ω）进行抽样的结果，即

-0.5Δω≤δωp≤0.5Δω，将式（18）代入式（13）和式（14）得p次谐波，则p次谐波的幅值和相位分别为

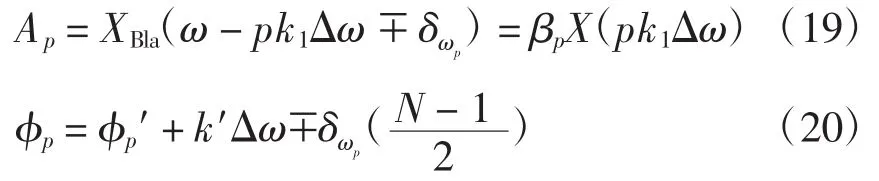
式中，φp′为电力p次谐波信号的FFT离散频谱的主谱XBla（kpΔω）的相位。

3 仿真实验

本文采用的仿真软件为Matlab7.7.0（R2008b）。仿真采用的信号模型为

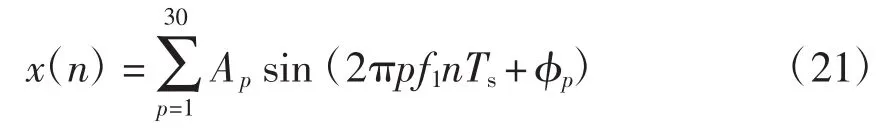
式中：基波频率f1为50.4Hz；采样频率fs为6400Hz，截断信号的数据长度N为1 280点；电力信号的参数如表1所示。

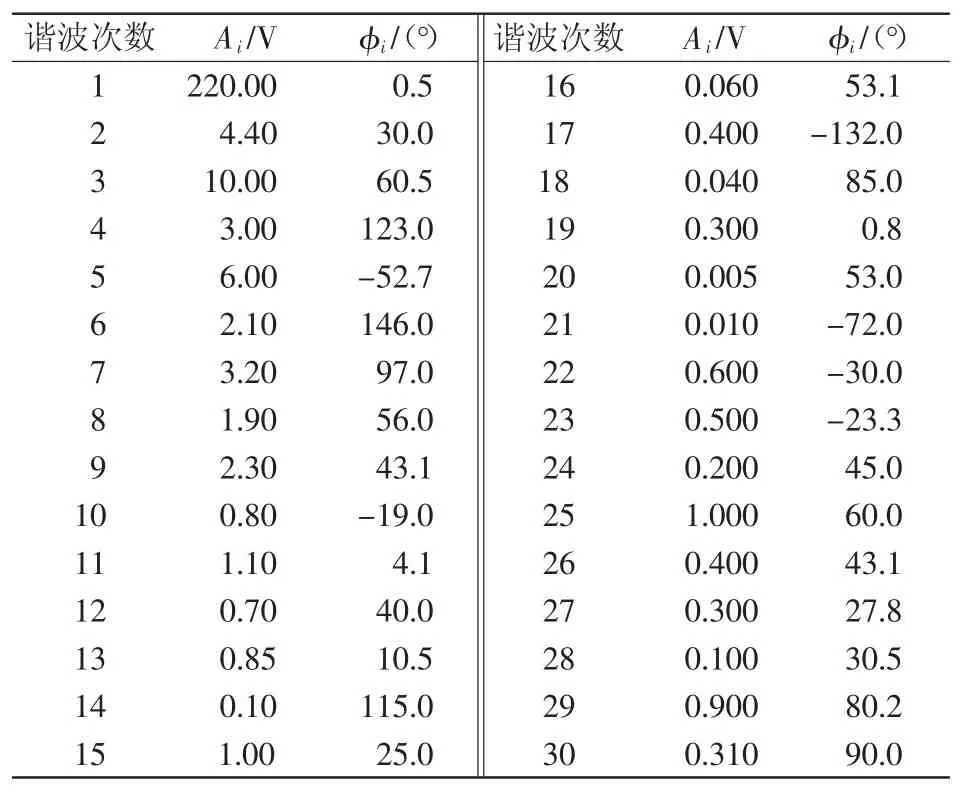
表1 仿真信号的基波及谐波成分Tab.1Components of the simulated harmonic signal

利用CZT，取M=N=1 280，高精度估计出基波频率、幅值和相位分别为f1=50.400 000 Hz，A1= 220.004 3 V，φ1=0.499 3°。

如图5所示，本文提出的分析方法与基于Blackman窗的双谱线插值拟合法具有基本同等的分析精度。用同一台计算机和同一个仿真软件进行计算，两种方法计算耗时分别为7.889 ms和15.830 ms，本文所提方法计算时间减少了一半。

图5 幅值与相位绝对误差对比Fig.5Comparisons of absolute errors in calculating amplitude and phase

4 结语

本文提出了一种电力谐波分析的新思路，即先高精度地估计出含有谐波的电力信号中的基波相量，进而，通过窗函数频域内插值的方法精确计算出各次谐波的校正系数，分别计算出各次谐波的参数。通过同一电力信号的仿真试验证明，它与加Blackman窗双谱线插值拟合估计电力谐波的分析方法有基本等同的估计精度，而这种算法在计算速度上有明显的优势，是一种很有实用价值的电力谐波进行高精度估计的方法。

[1]Mahmoud Aly A.Effects of power system harmonics on power system equipment and loads[J].IEEE Trans on Power Apparatus and Systems，1985，104（9）：2555-2563.

[2]Heydt G T，Fjeld P S，Liu C C，et al.Applications of the windowed FFT to electric power quality assessment[J]. IEEE Trans on Power Delivery，1999，14（4）：1411-1416.

[3]Hidalgo R M，Fernandez J G，Rivera R R，et al.A simple adjustable window algorithm to improve FFT measurements[J].IEEE Trans on Instrumentation and Measurement，2002，51（1）：31-36.

[4]门长有，王荣华，谭年熊（Men Changyou，Wang Rong hua，Tan Nianxiong）.一种用于谐波测量的全数字同步采样算法（An entire digital synchronous sampling algorithm for harmonic measurements）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（22）：83-86.

[5]吴静，赵伟（Wu Jing，Zhao Wei）.一种用于分析电网谐波的多谱线插值算法（An algorithm of MICA for analyzing harmonics in power system）[J].中国电机工程学报（Proceedings of the CSEE），2006，26（8）：55-60.

[6]Offelli C，Petri D.Interpolation techniques for real-time multifrequency waveform analysis[J].IEEE Trans on Instrumentation and Measurement，1990，39（1）：106-111.

[7]Agrez D.Weighted multipoint interpolated DFT to improve amplitude estimation of multifrequency signal[J].IEEE Trans on Instrumentation and Measurement，2002，51（2）：287-292.

[8]Xue H，Yang R.Optimal interpolating windowed discrete Fourier transform algorithms for harmonic analysis in power systems[J].IEE Proceedings of Generation，Transmission and Distribution，2003，150（5）：583-587.

[9]曾博，滕召胜，高云鹏，等（Zeng Bo，Teng Zhaosheng，Gao Yunpeng，et al）.基于Rife-Vincent窗的高准确度电力谐波相量计算方法（An accurate approach for power harmonic phasor calculation based on Rife-Vincent window）[J].电工技术学报（Transactions of China Electrotechnical Society），2009，24（8）：154-158.

[10]曾博，滕召胜，温和，等（Zeng Bo，Teng Zhaosheng，Wen He，et al）.莱夫-文森特窗插值FFT谐波分析方法（An approach for harmonic analysis based on Rife-Vincent window interpolation FFT）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（10）：115-120.

[11]卿柏元，滕召胜，高云鹏，等（Qing Baiyuan，Teng Zhaosheng，Gao Yunpeng，et al）.基于Nuttall窗双谱线插值FFT的电力谐波分析方法（An approach for electrical harmonic analysis based on Nuttall window doublespectrum-line interpolation FFT）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（25）：153-158.

[12]Reljin I S，Reljin B D，Papic V D.Extremely flat-top windows for harmonic analysis[J].IEEE Trans on Instrumentation and Measurement，2007，56（3）：1025-1041.

[13]庞浩，李东霞，俎云霄，等（Pang Hao，Li Dongxia，Zu Yunxiao，et al）.应用FFT进行电力系统谐波分析的改进算法（An improved algorithm for harmonic analysis of power system using FFT technique）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（6）：50-54.

[14]Rabiner L R，Schafer R W，Rader C M.The Chirp Z-transform algorithm[J].IEEE Trans on Audio and Electro-acoustics，1969，17（2）：86-92.

[15]GB/T 15945 2008，电能质量电力系统频率允许偏差[S].

New Calculation Method of Electric Power Harmonic in Frequency Domain Interpolation of Blackman Windows

TANG Yi，CHEN Kui，HAN Zhi-qiang，CHEN Lei，YANG Luo
（School of Information and Electrical Engineering，China University of Mining and Technology，Xuzhou 221008，China）

In this paper，a new method with high accuracy for electric harmonic estimation is presented.First，the CZT（Chirp Z-transform）is used to extract the parameters（amplitude，frequency and phase）of fundamental frequecy signals precisely from the multifrequency signals of power system.Second，after subtracting the fundamental frequency signal from the multifrequency signals，the harmonic signals are truncated with the Blackman window and their spectrums are calculated by fast Fourier transform（FFT）.Then，according to the fundamental frequency，each frequency harmonic is calculated.At last，interpolating on the frequency domain of the Blackman window，the parameters（amplitude and phase）of each frequency harmonic signals can be calculated precisely.The simulation results show that the proposed method almost has the same estimation accuracy with the method which is based on double-spectrum-line interpolation FFT，but the new method only costs about half computation times.

Chirp Z transform；fast Fourier transform（FFT）；harmonic analysis；Blackman window；interpolation on frequency domain

TM935-470.40

A

1003-8930（2013）03-0142-05

唐轶（1957—），男，博士，教授，博士生导师，从事电力系统自动化和电能质量控制领域的教学、研究工作。Email：tangyi@cumt.edu.cn

2011-06-14；

2011-08-17

江苏省科技支撑计划（工业）资助项目（BE2012042）

陈奎（1973—），男，博士，副教授，从事电力系统自动化方面的教学和研究工作。Email：chenkui73@cumt.edu.cn

韩智强（1987—），男，硕士研究生，从事电能质量的监测与控制的研究。E-mail：hzqiang87@163.com