小波包变换在风电场谐波分析中的应用

解胜民，杨秀媛

（北京信息科技大学自动化学院，北京 100192）

小波包变换在风电场谐波分析中的应用

解胜民，杨秀媛

（北京信息科技大学自动化学院，北京 100192）

含有变频器的风力发电机组在并网发电时会给电力系统注入时变谐波。快速傅里叶变换（FFT）是目前谐波分析的主要方法，但是它不适合处理非平稳时变信号。提出利用小波包变换（WPT）的方法对电流信号进行分析。基于Daubechies小波，采用适当的采集频率和小波包分解树，使谐波频率落在小波包频带并利用其小波包系数重构出各次谐波。可以实现信号频带的均匀划分，能够更好地提取信号的时频特性，还具有分辨非平稳时变谐波的能力。仿真结果显示小波包变换的谐波分析能力更好，能根据要求分离任意次谐波。关键词：双馈风力发电机组；傅里叶变换；小波包变换；谐波分析；频率

随着我国经济的快速发展，对能源的需求越发强烈。但是传统的化石能源日益枯竭，并且由于大量的使用化石能源对自然环境造成了严重的污染。当前大力开发新的绿色替代能源显得尤为迫切，风力发电作为新能源产业的杰出代表得到快速的发展。近几年我国风力发电事业迅猛发展，装机容量不断扩大。大多数风机为变速恒频的双馈风力发电机组，其含有变频装置，部分输出功率通过交直交变频输出至电网。整流逆变给电网带来谐波污染，大量的谐波会对风电机组和风电场升压站的相关工作设备产生损害，如造成风电机组发电机、电容器、电缆等过热，降低运行寿命，严重的甚至会使风电场主变压器过热，甚至造成损坏[1，2]。谐波严重时还会导致风电机组的继电保护装置误动作，造成风机停机故障。

1 风电场谐波检测

1.1 谐波检测标准

目前对风电场内风机并网时的谐波检测的测试标准主要是IEC 61400-21。该标准主要是对含有电力电子变换装置机组的谐波进行检测，要求测量频率在50倍电网基准频率以内的各次谐波电流和最大谐波电流畸变率。标准规定总谐波畸变率THD（total harmonic distortion），计算公式为

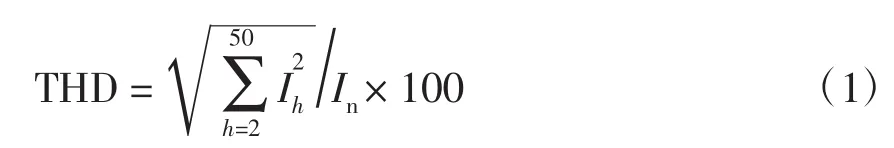
式中：Ih为风电机组h次谐波电流有效值；In为风电机组额定电流。

标准还规定了连接到公共连接点上的多台风电机组引起的谐波电流的计算公式为

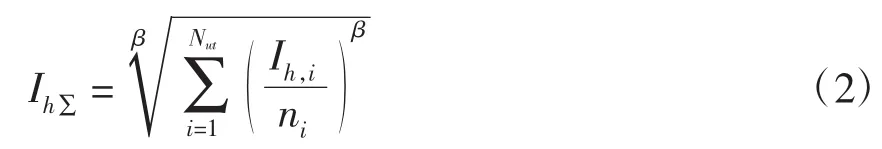
式中：IhΣ为公共连接点上的h次谐波电流畸变；Nwt为连接到公共连接点上的风电机组的数目；ni为第i台风电机组变压器的变比；Ih，i为第i台风电机组h次谐波电流畸变；指数β的规定如表1所示。

表1 指数β的规定Tab.1Specification of exponentβ

利用式（2）能够由各台风机处的电流谐波计算出公共连接点处的谐波情况，保证注入公共连接点处的谐波电流不超过国家规定的限值[3]。

1.2 谐波分析现状及面临的问题

目前谐波分析主要是利用傅里叶变换进行分析。对于确定信号和平稳信号，傅里叶变换是信号分析的理论基础，有着非凡的意义，起着重大的作用。傅里叶变换的正变换公式定义为

傅里叶变换把时间域与频率域联系起来，通过研究f（ω）来研究f（t），在时域内难以看清的问题，在频域中往往表现得非常清楚。

由于傅里叶变换只有频域局部性，不具有时域局部性，如果信号中含有突变的、非平稳的扰动信号，傅里叶变换的结果不能反映扰动信号的时域细节，而且此时使用傅里叶变换还会产生频谱混叠效应和栅栏效应，使测量精度变低[4，5]。

风速和风向的随机性会造成风机输出功率的波动，风电机组含有的变流器一直处于工作状态，就会产生谐波电流，并且谐波电流中可能含有突变谐波。利用傅里叶变换进行分析不能反映实际电流中各次谐波的时域情况，并且由于频谱混叠和栅栏效应的存在，测试精度会受到影响。小波包变换因具有良好的时频局部性，不仅能够有效地提取谐波信号的时域情况，而且能够对突变谐波分量进行有效地提取，是一种良好时频分析工具，非常适合风力发电的谐波检测[6]。

2 小波包变换

2.1 小波包变换的定义

小波包变换WPT（wavelet package transform）在信号的低频和高频部分均进行了细分，能够将信号频带进行均匀地划分，能够更好地提取信号的时频特性。由于小波包变换对信号的高频部分也进行了细分，故对信号的分析能力更强，小波包变换是一种更广泛、更精细的分解方法。

小波包定义为设{hn}n∈z是正交尺度函数φ（t）对应的正交低通实系数滤波器，{gn}n∈z是正交小波函数ψ（t）对应的高通滤波器，其中gn=（-1）nh1-n。它们满足两尺度方程和小波方程，即

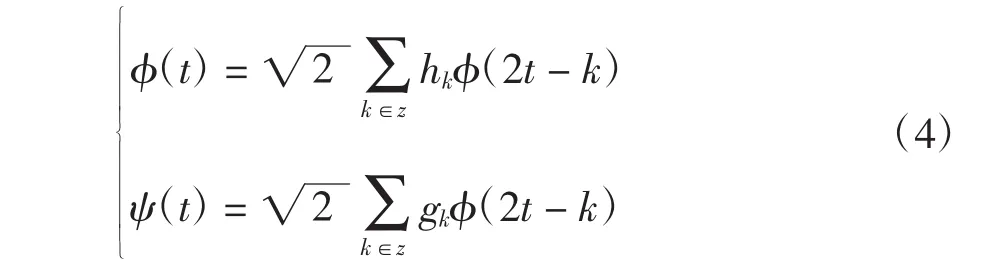
令μ0（t）=φ（t），μ1（t）=ψ（t），则式（4）为

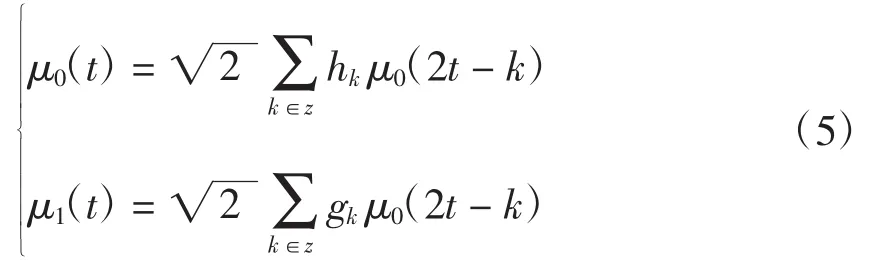
在固定尺度下通过μ0、μ1、h、g定义一组小波包函数为

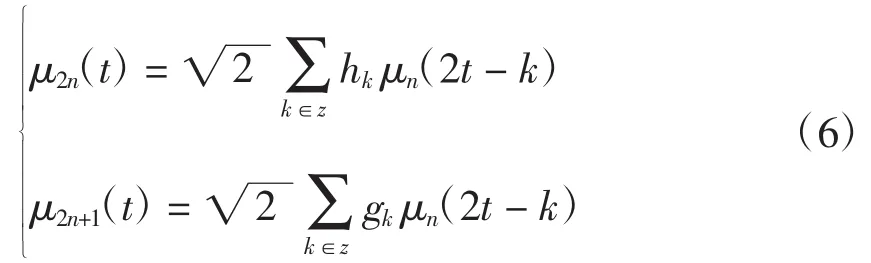
递归定义的函数μn（n=0，1，2，…），称为由正交尺度函数μ0=φ确定的小波包[7]。

通过离散小波变换的滤波器组来计算出小波包系数，图1为小波包分解树形结构，图2为小波包重构树形结构[8]。

2.2 小波包变换的频带

小波包变换后的频带次序并不是按照频率递增的规律来排序的，其频带排序规则是低频系数的分解对应着先低后高的排序次序，高频系数的分解对应着先高后低的排序次序。若用0表示L，1表示H，4层小波包变换结果[9]如图3所示。

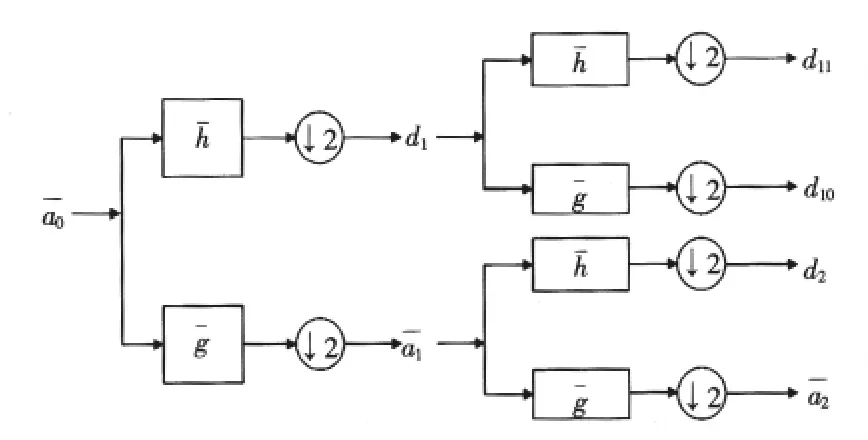
图1 小波包分解树形结构Fig.1Structure of the WPT decomposition tree

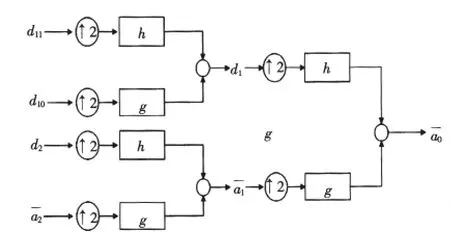
图2 小波包重构树形结构Fig.2Structure of the WPT reconstruction tree

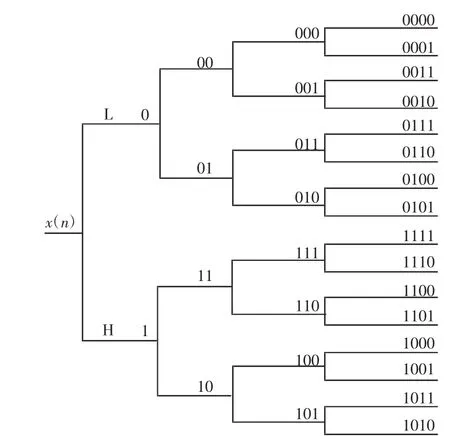
图3 4层小波包分解Fig.3Four level WPT decomposition

3 算例仿真实验分析

待分析的信号为风电场内某双馈风电机组并网点处实际采集的电流信号（电流信号的采集位置位于风机出口处，设备的采集频率为4 kHz）。待分析的实际电流信号波形如图4所示。

利用傅里叶变换、小波包变换分别进行各次电流谐波分析，具体分析结果如下。

3.1 傅里叶变换分析

利用Matlab编程对实际电流信号进行FFT变换，变换后得到的频谱如图5所示。将100～450Hz频率范围曲线放大得图6。

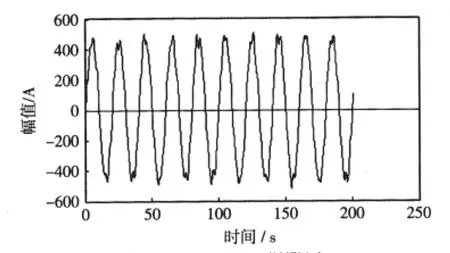
图4 实际电流信号波形Fig.4Actual current signal waveform

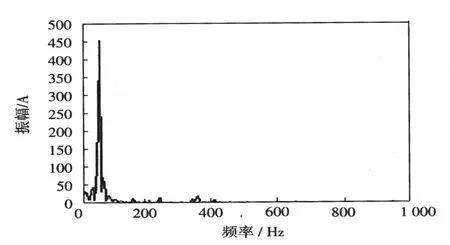
图5 FFT变换频谱Fig.5FFT transform spectrum

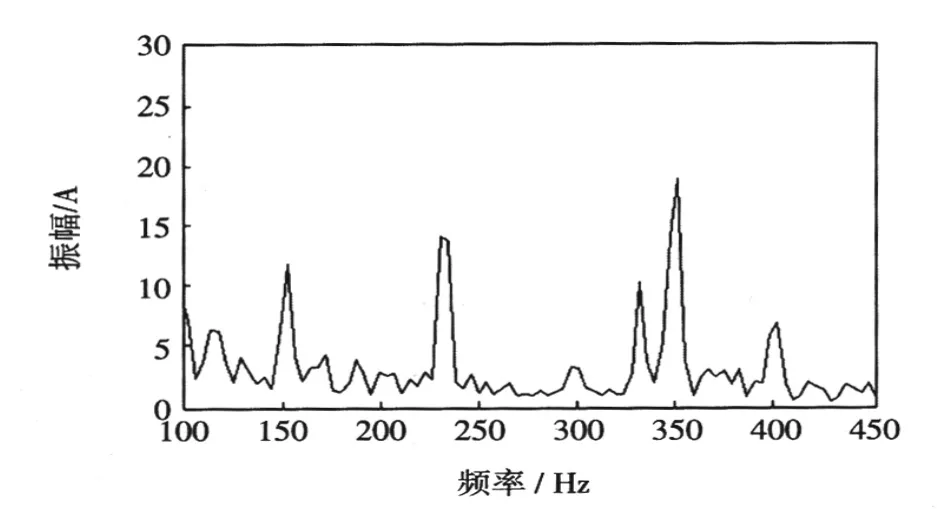
图6 放大频谱Fig.6Amplification spectrum

由图5可以看出，原始信号经过傅里叶变换后转换成纯频域信号。通过对频谱的研究可知，在50 Hz处有较强的信号，其信号幅值为453.7 A，可以得出原始信号中含有的主要成分为基波。通过局部放大图6可知在100、150、250、350、400 Hz处有较弱信号，其各次谐波电流对应的幅值见表2。

由表2可得3次、5次、7次谐波较大，其中7次谐波最大，2次谐波可能受到频率泄露的影响显示偏大。原始信号中含少量上述频率的谐波，根据各频率处谐波幅值的大小可以确定各次谐波的有效值，并可求出各次谐波的谐波畸变。综合可知，傅里叶变换具有良好的频域局部性，但是不再具有时域分辨能力。信号中含有的突变频率成分无法通过傅里叶变换表现出来，这是由于傅里叶变化的积分作用平滑了非稳定的突变成分。

表2 谐波电流幅值Tab.2Harmonic current amplitude

3.2 小波包变换实验分析

采用db30小波进行6层小波包变换，原始信号中可能包含较高次数的谐波。表2所覆盖的频带范围已包含原始信号的基波到8次谐波。小波包变换的各层所占的频带和包含的谐波信息如表3所示。从分解系数所对应的频带范围可以看到分解系数所对应的频带并没有按照大小顺序依次排序的。其排序规则，如前面所介绍的一样是低频系数的分解对应着先低后高的排序次序，高频系数的分解对应着先高后低的排序次序。

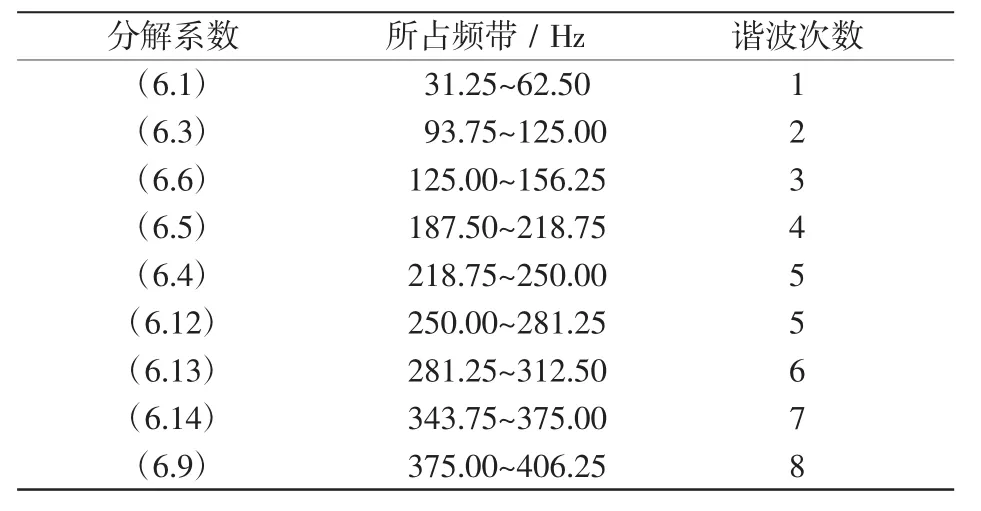
表3 小波包变换各层所占频带和包含的谐波信息Tab.3WPT layers occupy bands and contain the harmonic information

小波包分解后重构的各次谐波信号如图7～图14所示。

由图7可得基波分量在时域内被准确的提取出来。基波仿真分析曲线无异常波动表明风电机组运行平稳，风机出力无较大变化。小波包变换结果中2次谐波较FFT变换结果大，这可能是由于频谱混叠造成的。由3～8次谐波的仿真可得风电机组中的奇次谐波3、5、7次谐波较大，尤以5、7次谐波分量大。偶数次谐波均较小，4、6、8次谐波中4次谐波最大，8次谐波最小，偶数次谐波随着次数的增加逐渐变小。通过小波包变换结果可得并网运行的风电机组产生的电流谐波主要为奇次谐波。

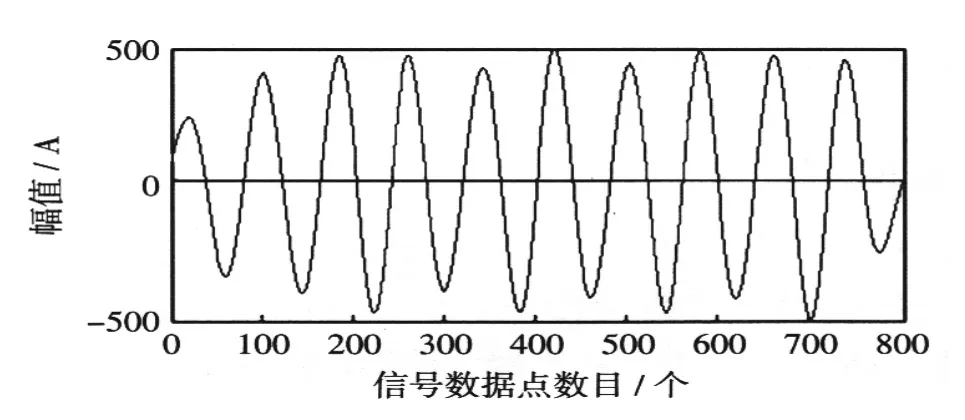
图7 基波Fig.7Fundamental

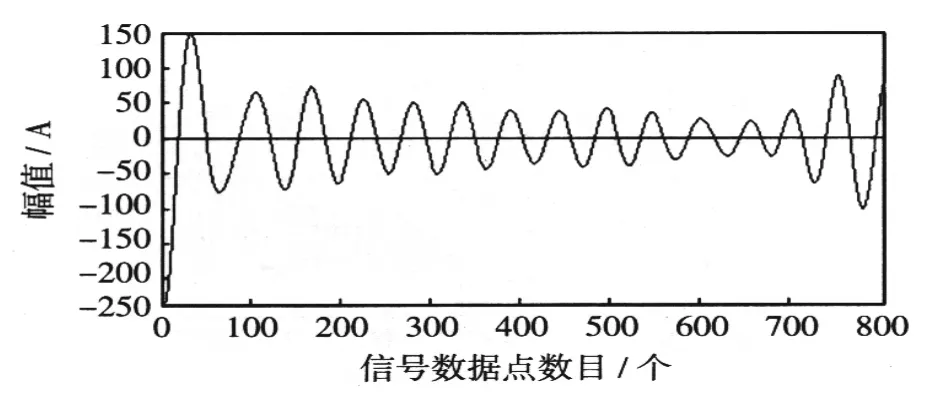
图8 2次谐波Fig.8Second frequency harmonic

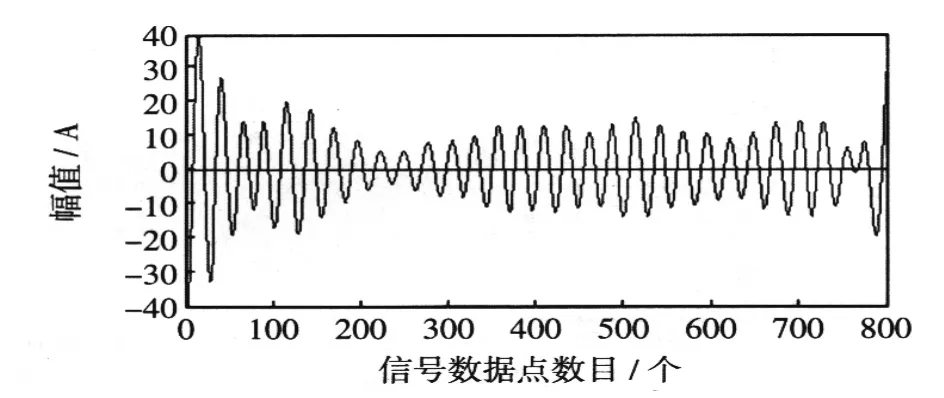
图9 3次谐波Fig.9Third frequency harmonic

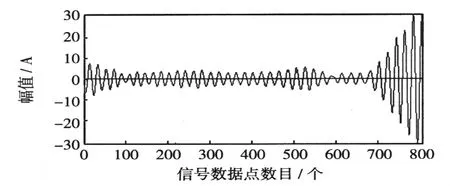
图10 4次谐波Fig.10Fourth frequency harmonic

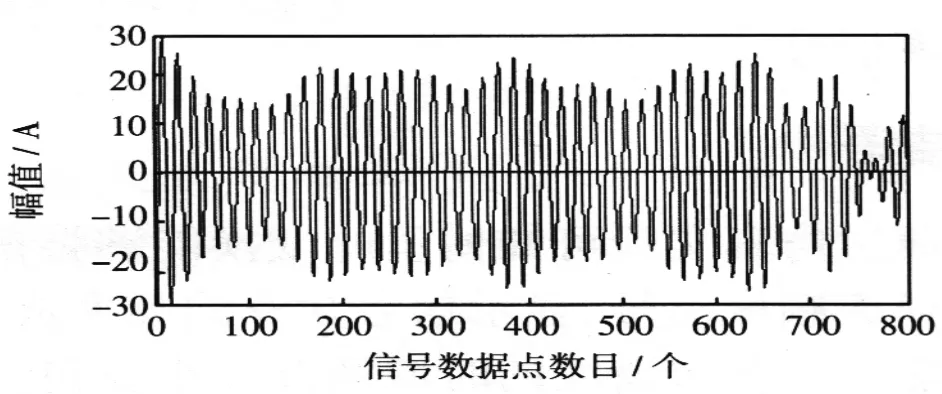
图11 5次谐波Fig.11Fifth frequency harmonic

图12 6次谐波Fig.12Sixth frequency harmonic

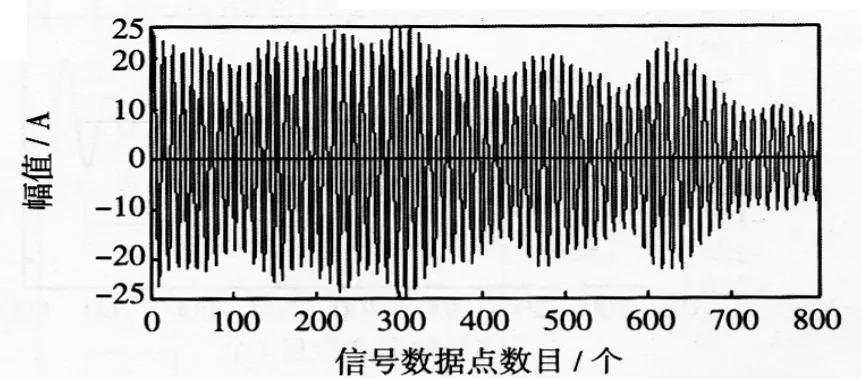
图13 7次谐波Fig.13Seventh frequency harmonic

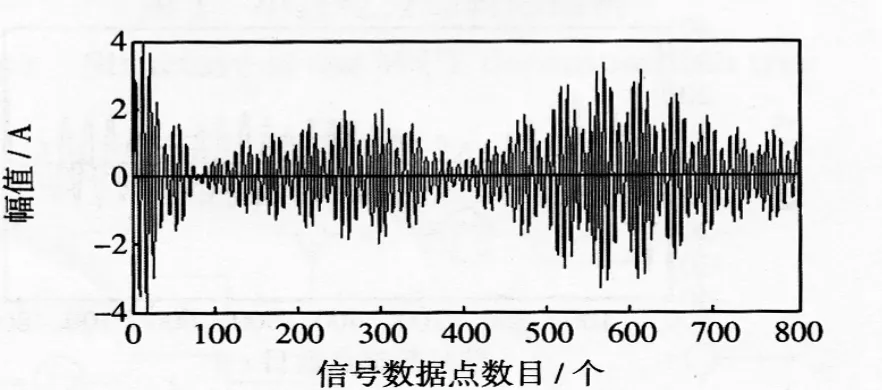
图14 8次谐波Fig.14Eighth frequency harmonic

由各次谐波仿真图像对比FFT变换的结果可以看出两者都有效地提取了信号中的各次谐波，但是小波包变换能够在时域内显示各次谐波的情况，这是其重大优点。小波包变换分析结果不仅具有频域的局部化能力，还能够准确地提取各次谐波的时域信息，非常适合分析具有突变成分的实际电流信号。

4 结语

通过仿真实验可知傅里叶变换能够将信号完全转换成频域信号，显示信号含有的频率成分，但是不能显示各次谐波的时域情况。小波包变换弥补了傅里叶变换的不足，不仅能够精确地提取基波分量和各次谐波分量，并且能够将在时域内显示各次谐波。实际信号中某些分量发生突变时，利用傅里叶变换并不能确定突变的具体起始时刻，而利用小波包变换则能有效地提取各次分量的时域信息，确定分量发生突变的具体时间。通过对风电机组并网电流分别进行傅里叶变换和小波包变换，可得风电机组电流谐波主要为次数较低的奇次谐波，偶数次谐波通常较小。这也为以后的谐波补偿和抑制打下基础。

[1]林永，劳伟筹（Lin Yong，Lao Weichou）.风电场对电网的电能质量影响研究（The research of the impact of wind farm integratio n on power grid）[J].电气应用（Electrotechnical Application），2009，28（21）：42-45.

[2]李瑜，范高峰，李庆，等（Li Yu，Fan Gaofeng，Li Qing，et al）.达坂城风电接入系统对新疆电网电能质量的影响（The impact of Dabancheng wind farm integration on power quality of Xinjiang power grid）[J].电网技术（Power System Technology），2007，31（6）：88-92.

[3]IEC 61400-21，Measurement and assessment of power quality characteristics of grid connected wind turbines[S]．

[4]忻黎敏，许维胜，余有灵（Xin Limin，Xu Weisheng，Yu Youling）.基于递推离散傅里叶变换和同步采样的谐波电流实时检测方法（A real-time harmonic current detection method based on recursive discrete Fourier transform and synchronous sampling）[J].电网技术（Power System Technology），2008，32（6）：14-18.

[5]庞浩，李东霞，俎云霄，等（Pang Hao，Li Dongxia，Zu Yunxiao，et al）.应用FFT进行电力系统谐波分析的改进算法（An improved algorithm for harmonic analysis of power system using FFT technique）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（6）：50-54.

[6]陈建军，龚南斌（Chen Jianjun，Gong Nanbin）．风力发电并网对电力系统电能质量的影响分析（Analysis on influence of wind power integration on power quality）[J].华北电力技术（North China Electric Power），2010，12（5）：10-13.

[7]黄文清，戴瑜兴，全慧敏（Huang Wenqing，Dai Yuxing，Quan Huimin）.基于Daubechies小波的谐波分析算法（Harmonic estimation method basedonDaubechies wavelet）[J].电工技术学报（Transactions of China Electrotechnical Society），2006，21（6）：45～48，53.

[8]刘平英，刘国海（Liu Pingying，Liu Guohai）.基于小波包变换的电力系统谐波分析（The harmonic analysis in power system based on wavelet transform）[J]．微计算机信息（Microcomputer Information），2008，24（2-1）：276-278.

[9]薛蕙，杨仁刚，郭永芳（Xue Hui，Yang Rengang，Guo Yongfang）.小波包变换（WPT）频带划分特性的分析（Frequency division character of wavelet packet transform）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（2）：5-8.

Application of Wavelet Packet in Harmonic Analysis for Wind Power Plants

XIE Sheng-min，YANG Xiu-yuan
（AutomationCollege，BeijingInformationScienceandTechnologyUniversity，Beijing，100192，China）

The wind turbine containing the inverter under grid connected mode will inject time-varying harmonic current into the power system.The fast Fourier transform（FFT）is currently the main method for the electrical harmonic analysis while it is not suitable for analyzing time-varying signals.A novel method for analyzing the current signal based on the wavelet packet transform is proposed.Based on the db wavelet，this method makes use of appropriate sampling frequency and the tree of the wavelet packet decomposition.The harmonic frequency tested will locate in the frequency band and the harmonic is reconstructed by using the wavelet packet coefficient.Using wavelet packet transform，the frequency band of signal can be uniformly divided and the signal features in time domain and frequency domain are extracted better.WPT also has the ability to distinguish non-stationary time-varying harmonic possesses for harmonic analysis.The result of the simulation shows that the wavelet packet transform is more effective in the analysis of the harmonic.WPT can even extract any times of harmonics.

doubly-fed wind turbine generator system；Fourier transform；wavelet packet transform；harmonic analysis；frequency

TM714

A

1003-8930（2013）03-0162-05

解胜民（1985—），男，硕士研究生，研究方向为大型双馈异步风电机组谐波分析与控制。Email：xsm1985@163.com

2011-11-21；

2011-12-16

杨秀媛（1962—），女，副教授，研究方向为新能源系统与控制。Email：yangxy0912@sohu.com