含风电机组的配电网电容器投切

王威，韩学山，李保银

（1．山东科技大学机电工程系，泰安 271019；2．山东大学电气工程学院，济南 250061）

含风电机组的配电网电容器投切

王威1，韩学山2，李保银1

（1．山东科技大学机电工程系，泰安 271019；2．山东大学电气工程学院，济南 250061）

针对含出力不确定的风电机组配电网电容器投切问题，提出基于多场景技术的电容器投切方法。将网络划分为多棵局部树，在回推潮流计算后增加局部树的电容器投切，优化模型为凸二次整数规划，采用分支定界法快速求解。根据风机功率只有变化到一定程度时，电容器投切组数才改变的特点，给出快速获得Monte-Carlo模拟的每个场景优化方案算法，不必一一优化每个场景。这样，每个方案包含多个场景，取场景乘以其发生概率后求和所得值最大的方案为投切方案。算例结果验证了算法的有效性。

配电网络；电容器投切；局部树；风电机组；多场景技术

分组、分级的电容器是配电网无功补偿的重要组成部分。在实时运行中，根据实际负荷水平，在一定目标下，确定电容器投切的最优方案[1～5]，可以有效地降低网损，提高电力企业的效益。但近年来随着风电机组并入配电网，其发电量的不确定性，传统的确定性条件下的方法不能完全适用，电容器投切就转化为在不确定条件下的优化决策问题。

文献[6，7]研究了含分布式电源的配电网电容器投切问题，但把DG看作并网节点上的功率值为负值的负荷，没有考虑其输出功率的随机性。

风速的随机性导致风机出力的不确定，需结合不确定性理论研究含风电机组的配电网电容器投切。场景分析法[8]是解决该问题的一种有效方法。文献[9]提出基于场景发生概率的无功优化模型，给出3个典型场景及其发生概率，取优化方案使所有场景发生概率与该场景下目标函数乘积之和达到最优，对风电机组输出功率的随机变化具有较好的适用性，但是其目标函数决定了算法是一种平均意义上的最优。文献[10]提出的全场景下所得的无功优化方案，虽然并不满足各场景下的最优，但该方案满足各场景的运行约束，是整体最优的方案。

本文在结合多场景技术并考虑计算效率的前提下，研究了含风电机组的配电网电容器投切问题。

1 基于前推回推算法的配电网电容器投切

1.1 局部树

前推回推算法参见文献[11]。根节点或电容器节点与其相邻的下游电容器节点之间的所有节点和支路构成它们的局部树，对于电容器节点下游没有电容器的情况，则该电容器与其下游的节点和支路构成局部树。

根据以上局部树的定义，给出图1简单配电网络几个局部树，根节点的局部树包含节点1、2、3、14、15，支路1、2、13、14；电容器节点3的局部树包含的节点3、4、5、10、11，支路3、4、9、10；电容器节点7包含的节点7、8、9，支路7、8。

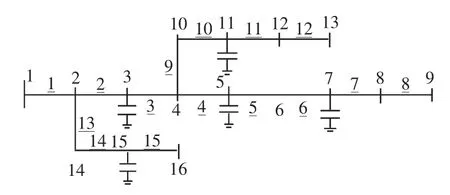
图1 简单的配电网络Fig.1Simple distribution network

局部树的形成方法：广度优先搜索[12]网络重新编号节点和支路的过程中，根据定义从根节点开始逐个取出局部树。优点是按局部树的逆序对每个局部树进行回推计算就是对整个网络的回推计算，为后面的基于前推回推潮流的电容器优化投切算法提供了实现的可能。

1.2 局部树的电容器优化投切分析

如图2所示局部树，有n+1个电容器。

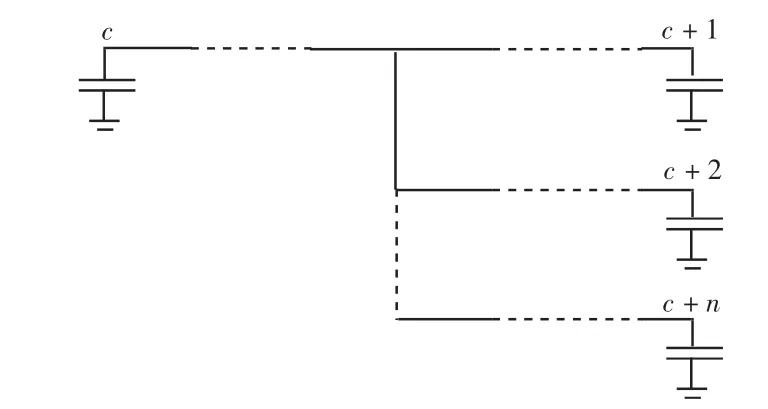
图2 局部树示意Fig.2Sketch of a local tree

由于第c个电容器在根节点上，电容器投切问题就是求电容器c+1，c+2，…，c+n投入组数，使局部树网损达到最小。

设第c+k（k=1，2，…，n）个电容器所在节点电压是ec+k，i+j fc+k，i，i是第c+k个电容器所在节点；第c+k个电容器投入的容量Qc+k=Kc+kQc+k，0，Qc+k，0是第c+k个电容器的单组容量，Kc+k是投入组数。则该电容器向网络中补偿的电流为

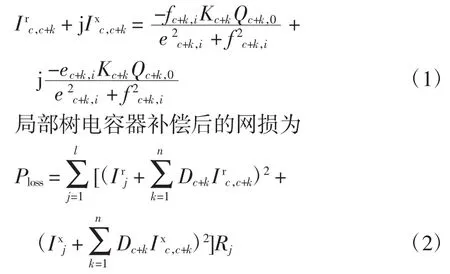
式中：l是支路数；Irj、Ixj是支路j电流的有功分量和无功分量；若第c+k个电容器所在节点到第c个电容器所在节点的路径上有支路j，Dc+k=1；否则，Dc+k=0；Rj是支路j的电阻。

将式（1）代入式（2），同时考虑电容器投入组数的上限约束，得电容器投切的目标函数为

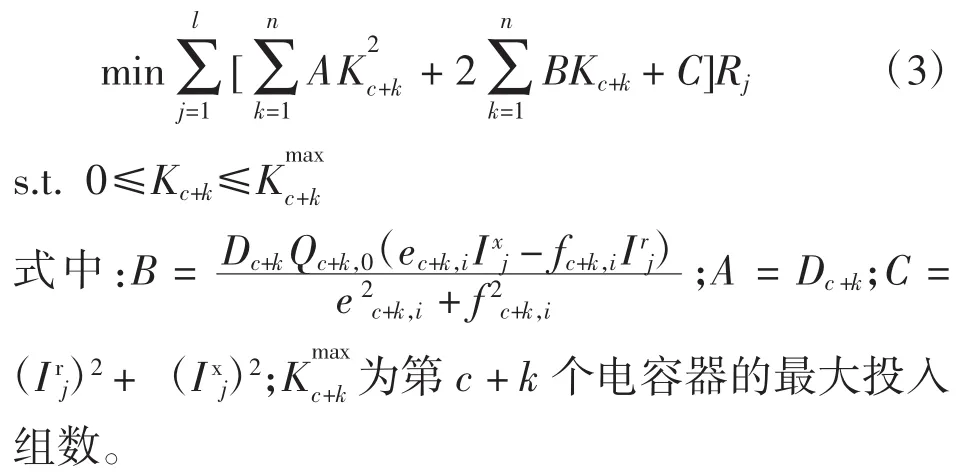
若式（3）中的节点电压已知，由于A=1，二次项海森矩阵正定，为凸二次整数规划，可采用文献[13]的分支定界算法计算。由于实际网络中每棵局部树上电容器个数n通常很小，考虑到电容器投入组数约束，分支定界法的计算效率高。

当计算完第c+1，c+2，…，c+n个电容器投入组数后，根据无功功率平衡的原则，第c个电容器向下游补偿的无功功率Qc是局部树总的无功负荷与无功网损之和再减去电容器c+1，c+2，…，c+n补偿的无功功率。

1.3 基于前推回推的电容器投切算法

基于前推回推算法的电容器投切算法的思想是：在回推计算后，根据节点电压不变的条件，对局部树按照第1.1节生成顺序的逆序按照式（3）逐个优化，当前推回推算法收敛后即可得到电容器的投入组数。

下面以图1中节点7上电容器投入组数计算为例，说明计算过程中需要注意的问题。首先计算节点7向下游投入的容量，而这个容量并不一定是电容器单组容量的整数倍，得到的电容器投入组数是小数；再根据第1.2节优化节点5上电容器对应的局部树，得节点7上电容器向上游投入的组数，这样节点7上电容器投入组数为向下游和上游投入组数之和。由于向下游投入组数是小数，仍然需归整，影响解的精度，为此，在得到节点7上电容器的向下游投入组数后归整，方法是整数部分加1。这样多余的无功补偿节点7上游就近的无功负荷，符合电容器就地补偿负荷的特点，同时根据节点7的电压计算多余的无功功率，计算后的有功电流分量和无功电流分量叠加到节点5的电容器对应的局部树的支路上。这样节点7上电容器向下游投入的组数是整数，向上游投入的组数也是整数，二者相加为节点7上电容器的投入组数。

下面给出基于前推回推算法的电容器投切算法步骤。

步骤1广度优先搜索重新编号节点和支路，并取出逐个局部树；

步骤2设各节点电压为1，不考虑电容器补偿的条件下，回推计算支路电流；

步骤3按取出的局部树逆序逐个优化局部树，具体步骤如下：

（1）将第c+1，c+2，…，c+n个电容器向下游补偿的投入组数取整加1，并将多出的无功功率计算成补偿电流叠加到局部树根节点到第c+k个电容器所在节点之间的路径上；

（2）按式（3）优化局部树得电容器c+1，c+2，…，c+n向上游的投入组数，再加上其向下游归整后的投入组数得总的投入组数，并计算电容器投入后各支路的电流；

（3）根据无功功率平衡的原则计算电容器c向下游投入的组数；

（4）前推电压计算，若满足潮流收敛条件结束；否则，返回步骤3。

算法的优点是前推回推潮流和式（3）凸二次整数规划保证了算法的准确性和良好收敛性。

电容器的投切组数是整数，负荷的变化并不一定引起投切组数的改变，对于多个负荷值电容器优化投切后的投切组数是相同的。也就是说，同一个优化方案对应多个场景。

2 多场景技术的含风电机组配电网电容器投切

2.1 基于Monte-Carlo模拟法的场景预测

与负荷变化相比，风电机组输出功率的变化更加频繁，且目前风速还很难精确预测[14]，为了突出风电机组对配电网电容器投切的影响，不考虑负荷变化，只考虑风电机组输出功率的随机变化。

目前风速的概率预测通常采用Weibull分布[15，16]，Weibull分布是对风速长期预测，但电容器投切是在线进行的，短时预测最好根据当地天气预报的风速预测结果。但为了研究方便，假定风速服从正态分布N（μ，δ2），μ是服从正态分布的随机变量风速的均值，δ是此随机变量的方差。

在风速服从正态分布的条件下，基于Monte-Carlo模拟法[17]的场景预测过程如下：

（1）应用非序贯Monte-Carlo模拟法可产生个服从正态分布N（μ，δ2）的风速，进而计算出该风速下风机输出功率，即得到n个场景；

（2）对第i（i=1，2，…，n）个场景，应用第1.3节基于前推回推的电容器投切算法计算该场景的电容器投切组数。

2.2 每个场景的优化方案的确定

由于场景个数过多，若采用第1.1节的方法逐个优化场景计算效率低，根据第1.2节的分析，只有在风机输出功率变化到一定值时电容器投切方案才改变，给出快速确定每个场景的优化方案的算法如下。

步骤1对Monte-Carlo模拟得到的场景，按风机出力由小到大排序，分别记作S1，S2，…，Sn，n为场景数。

步骤2分别优化S1、Sn得到电容器投切方案A1、An。

步骤3若A1=An，结束，即所有场景的优化方案相同。

步骤4若S1、Sn对应的风机出力之差的绝对值小于给定的ε（ε〉0），结束；若A1≠An，取风机出力为场景S1和Sn的风机出力中间的场景S1（n〉i〉1），优化Si得到电容器投切方案Ai。

步骤5若Ai≠A1且Ai=An，则场景Si与Sn之间的优化方案都相同，对风机出力在场景Si与Sn的之间的场景不再优化，取An，An代替Ai转向步骤4。

步骤6若Ai≠An且Ai=A1，则认为场景Si与S1之间的优化方案相同，对风机出力在场景Si与S1的之间的场景不再优化，取A1，A1代替Ai转向步骤4。

步骤7若Ai≠An≠A1，在Ai与An之间，A1代替Ai转向步骤4；在A1与Ai之间，An代替Ai转向步骤4。

若多个风电机组由同一风电场接入配电网，考虑到同一风电场的风速差异不大，可以假定各风电机组的风速分布相同。若同一个风电场内每个风机的参数、转速特性曲线和风速功率特性曲线相同，可把风电场看作是一台风机，应用以上算法快速计算；反之，若同一风电场内各风机参不同，必须考虑它们之间的相关性，即考虑到在相同风速条件下各个风机出力之间的差异及对电容器投切结果的影响，应对模拟的每个场景分别计算电容器投切结果，在这种条件下，为了提高计算速度，可以根据实际运行经验尽量减少模拟场景的个数。

2.3 配电网优化方案的确定

场景概率发生最大的方案，对应运行方式出现的概率及其运行时间是最大的，在风速服从正态分布的情况下，模拟的风速越接近给定的均值，认为该风速下对应的场景发生的概率越大。同样，优化方案包含的场景个数越多说明对风速的变化的适应度越高，优化结果更趋向于合理。

基于上述，应选择包含的场景个数多且场景发生的概率大的优化方案，同时考虑到若某个场景发生的概率很小，甚至不发生，若对其进行电容器投切意义不大。因此，给出选定优化方案的目标函数为

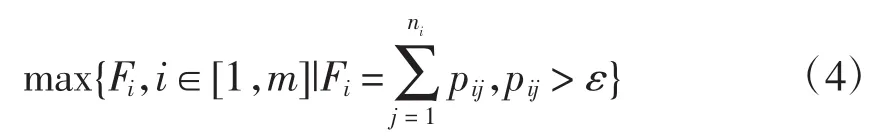
式中：Fi为第i个优化方案；m为方案数；ni为第i个方案的场景数；pij为第i个方案中第j个场景发生的概率；ε为预先给定的很小的概率值。

3 算例及分析

本文算法用c++语言编程，在Intel Pentium（D）CPU 2.80 MHz计算机实现，以图3的IEEE 69节点[16]网络为例。

3.1 电容器投切算例

在不考虑风机接入网络的条件下，采用第1.1节的方法得到投切组数如表1所示。

结果与文献[5，18]一致，由于本文采用数学规划方法求解，计算效率高于文献[5]的智能算法，相对文献[18]的在局部数组的优化过程中每次计算取减小值与单组容量比值最大的电容器增加投入一组容量的计算方法，本文的分支定界法直接求得电容器投切组数的整数解更加准确。

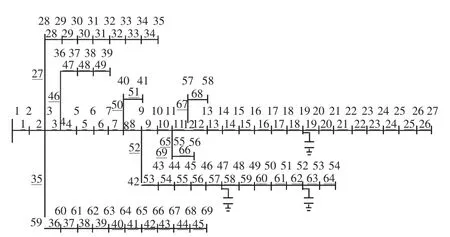
图3 IEEE 69节点系统Fig.3IEEE 69 nodes system

表1 电容器投切结果Tab.1Results of capacitor switching for 69 nodes

3.2 含风电机组的电容器投切算例

通常双馈异步发电机接在负荷处，目的是就地平衡负荷，该网络的50节点上负荷最大，因此假定在该节点上接入一个双馈异步发电机，其额定容量是1500kW，rs=0.001692Ω，rr=0.002423Ω，xs=0.036 92 Ω，xr=0.037 59 Ω，xm=1.456 8 Ω，同步转速是1000r/min。在风速服从正态分布N（10，4）的情况下，对风速进行了1 000次Monte-Carlo模拟，对模拟的风速，根据风机的转速特性曲线和风速功率特性曲线求得转差率S和发出功率Pe，再根据文献[19]的方法计算双馈异步发电机注入网络的有功功率和无功功率。

根据第2.2节的算法，只需21次而不是1 000次电容器投切计算就可得到如表2所示的电容器投切方案，计算时间11.7 s，基本可满足在线运行要求。

表2给出每个方案包含的场景个数，根据式（4）选择方案7作为最后的方案。

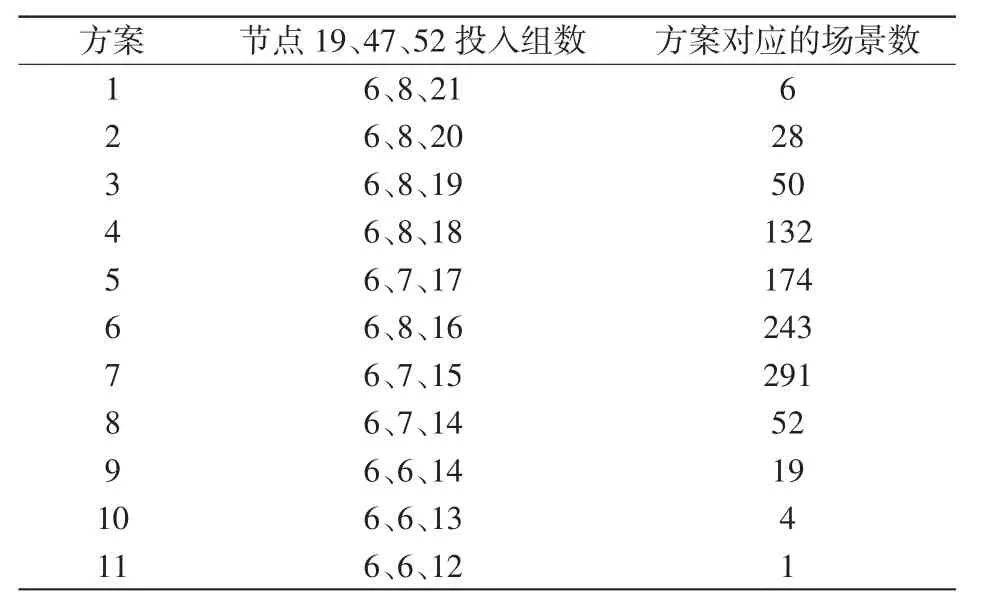
表2 Monte-Carlo模拟后的电容器投切结果Tab.2Capacitor switching results after Monte-Carlo simulation

4 结语

结合前推回推潮流算法和局部树优化的电容器投切算法，不仅收敛性好而且精度高。在基于前推回推算法的电容器投切算法基础上，给出的基于多场景技术的含风机条件下的电容器投切算法。最后选择包含场景最多且场景发生概率大的优化方案对风速的适应度更高。

[1]刘学平，刘天琪，李兴源（Liu Xueping，Liu Tianqi，Li Xingyuan）.含风电机组的配电网无功优化补偿（Optimal reactive power planning in distribution system with wind power generators）[J].电力系统保护与控制（Power System Protection and Control），2010，38（20）：130-135.

[2]刘伟量，黄纯，向为（Liu Weiliang，Huang Chun，Xiang Wei）.基于线性内点法的高中压配电网电压无功优化（Linear interior-point programming based voltage/reactive power optimization for high-medium voltage distribution networks）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（6）：82-87.

[3]王威，韩学山，王勇，等（Wang Wei，Han Xueshan，Wang Yong，et al）.配电网络电容器优化投切的作用范围法（Action scope algorithm for optimal capacitor switching in distribution network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（6）：36-40，69.

[4]杨洪，罗滇生，霍明（Yang Hong，Luo Diansheng，Huo Ming）.基于SA-PSO的配电网电容器优化配置（Optimal configuration of capacitors for radial distribution network based on simulated annealing particle swarm optimization algorithm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（3）：111-114.

[5]郝文波，汤奕，于继来（Hao Wenbo，Tang Yi，Yu Jilai）.基于交流支路电气剖分思想的配电网电容器优化投切方法（An optimal capacitor switching method of distribution network based on electrical dissection of AC branches）[J].电网技术（Power System Technology），2007，31（17）：41-46.

[6]Golshan M E H，Arefifar S A.Distributed generation，reactive sources and network-configuration planning for power and energy-loss reduction[J].IEE Proceeding-Generation，Transmission and Distribution，2006，153（2）：127-136.

[7]Singh D，Singh D，Verma K S.Multiobjective optimization for DG planning with load models[J].IEEE Trans on Power Systems，2009，24（1）：427-436.

[8]高赐威，程浩忠，王旭（Gao Ciwei，Cheng Haozhong，Wang Xu）.考虑场景发生概率的柔性约束电网规划模型（Electric power network flexible planning model based on the probability of scene occurrence）[J].中国电机工程学报（Proceedings of the CSEE），2004，24（11）：34-38.

[9]陈海炎，陈金富，段献忠（Chen Haiyan，Chen Jinfu，Duan Xianzhong）.含风电机组的配网无功优化（Reactive power optimization in distribution system with wind power generators）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（7）：40-45.

[10]何禹清，彭建春，毛丽林，等（He Yuqing，Peng Jianchun，Mao Lilin，et al）.含多个风电机组的配电网无功优化（Reactive power optimization in distribution system with multiple wind power generators）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（19）：37-41.

[11]车仁飞（Che Renfei）.配电网潮流计算及重构算法的研究（Studies on Power Flow and Network Reconfiguration for Distribution Systems）[D].济南：山东大学电气工程学院（Jinan：School of Electrical Engineering，Shandong U－niversity），2003.

[12]卢开澄，卢华明.图论及其应用[M].北京：清华大学出版社，1995.

[13]方述诚，普森普拉S.线性优化及扩展理论与算法[M].汪定伟，王梦光译.北京：科学出版社，1994.

[14]陈国初，杨维，张延迟，等（Chen Guochu，Yang Wei，Zhang Yanchi，et al）.风电场风速概率分布参数计算新方法（New computation method of wind speed probability distribution parameters in wind farm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：46-51.

[15]Feijoo A E，Cidras J.Modeling of wind farms in the load flow analysis[J].IEEE Trans on Power Systems，2000，15（1）：110-115.

[16]Baran M E，Wu F F.Optimal sizing of capacitors placed on radial distribution systems[J].IEEE Trans on Power Delivery，1989，4（1）：735-743.

[17]麻常辉，薛禹胜，王小英，等（Ma Changhui，Xue Yusheng，Wang Xiaoying，et al）．基于静态和动态安全风险的输电规划（二）计及注入功率的不确定性（Optimal transmission planning based on both static and dynamic risks part two with uncertain injection power）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（14）：10-13，61．

[18]任永峰，李含善，李建林，等（RenYongfeng，Li Hanshan，Li Jianlin，et al）.并网型双馈电机风力发电系统建模与仿真（Modeling and simulation of gird-connected DFIG wind power generation system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（5）：24-29.

[19]王威，韩学山，车仁飞，等（Wang Wei，Han Xueshan，Che Renfei，et al）.快速实用的配电网电容器优化投切算法（An efficient algorithm for capacitor switching in distribution network）[J].电网技术（Power System Technology），2010，34（5）：99-103.

Capacitor Switching of Distribution Network with Wind Turbines

WANG Wei1，HAN Xue-shan2，LI Bao-yin1
（1.School of Machine and Electric Engineering，Shandong Science and Technology University，Taian 271019，China；
2.School of Electric Engineering，Shandong University，Jinan 250061，China）

For capacitor switching in distribution network with uncertain output of wind turbines，this paper proposes a capacitor switching method based on multi-scenario technique.The network is divided into many local trees.The capacitor switching is performed for local trees after the process of backward/forward sweep algorithm.The capacitor switching mathematical model of local tree is twice integer.The capacitor switching need not to be performed when the power of wind turbine changes less.Based on the above conclusion the optimal solution for each scenario obtained by Monte-Carlo simulation can be fast determined.Thus it needs not to calculate each scenario.Thus each solution has many scenarios.The solution is the max value that is the sum of probability for each scenery.The calculation results verify the feasibility of the proposed algorithm.

distribution network；capacitor switching；local tree；wind turbines；multi-scenario technique

TM73；F123.9

A

1003-8930（2013）03-0077-05

王威（1974―），男，博士，讲师，从事配电网优化理论方面的研究。Email：wangwei-dongfang@163.com

2012-04-20；

2012-05-10

山东省优秀中青年科学家科研奖励基金项目（2011BSB01212）

韩学山（1959―），男，教授，博士生导师，从事电力系统调度与运行及电力市场运营的研究。Email：xshan@sdu.edu.cn

李保银（1974―），男，助理实验师，从事电气控制方面的研究。Email：13468002062@163.com