分区支持向量回归及其在负荷预测中的应用

谷云东，胡芳芳

（华北电力大学数理学院，北京 102206）

分区支持向量回归及其在负荷预测中的应用

谷云东，胡芳芳

（华北电力大学数理学院，北京 102206）

为解决局地短期电力负荷预测问题，给出了一种基于自适应聚类分区和支持向量机回归的多模型变结构负荷预测新方法。首先根据局地电力负荷的特点，使用模糊C均值聚类方法给出预测时间点的自适应分区；然后利用支持向量回归方法对不同分区分别构建预测子模型；最后提出一种基于仿真分析的模型评估和参数优化方法，在测试评估的基础上优化确定各子模型的参数，并适当调整各分区的结构。实验表明该预测方法比常用的神经网络预测方法具有更高的准确率和更强的鲁棒性。

负荷预测；分区支持向量回归；模糊C均值聚类；自适应分区；变结构；模型评估

作为电力系统规划的重要组成部分，电力负荷预测是电力系统经济运行的基础[1]。早期负荷预测主要依赖以回归技术和时间序列分析为代表的统计分析方法。这类方法的优点是模型计算量小且运行速度较快[2]，但这些模型的预测精度难以满足实际工程的要求，且由于模型不具备自适应学习能力，预测系统的鲁棒性没有保障。20世纪80年代，专家系统在负荷预测中得到了成功的应用[3]。20世纪90年代，以人工神经网络、模糊推理系统和支持向量机SVM（support vector machine）为代表的机器学习方法，因其具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力等方面的优势，被广泛应用于电力系统负荷预测[4～8]。2000年以来，多种预测方法的结合或者预测方法和优化技术的结合等综合优化预测渐渐成为主流[9～13]，滚动预测也得到越来越广泛的应用[14，15]。但由于影响电力负荷的因素众多、电力负荷的发展变化规律存在多样性和不确定性等特点，采用具有固定结构的单一模型难以给出准确的电力负荷预测，因此，多模型或变结构负荷预测渐渐引起关注。本文提出一种基于分区支持向量回归SVR（support vector regression）的变结构电力负荷预测方法。该方法首先利用模糊聚类实现预测时间点的自适应分区；然后对各分区分别用支持向量机方法构建预测子模型，使得预测达到较高的精度；借助测试分析优化各分区子模型的结构及多模型之间的衔接，形成整体协调的变结构负荷预测模型；最后借助实验分析验证了方法的有效性。

1 基于自适应聚类分区和支持向量机的多模型变结构负荷预测方法

1.1 自适应分区变结构负荷预测的主要思想

传统意义上的分区负荷预测通常是指直接按行政区域、地理位置或社会发展特点等划分预测区域，在不同的区域可以选择不同的参数构建各异的模型。这种方法能够更好地适应不同区域的负荷特点，显著改善模型的负荷预测的准确性。事实上，电力负荷模式除了具有空间分布上的差异之外，同样具有时间点上和时段上的差异。以局地日负荷为例，不仅工作日和节假日的负荷模式常常会有显著性差别，而且在同一日的24小时内，早晨、上午、中午、下午等不同的时段也往往具有不同的负荷模式。同样地，不同日期的同一时间点负荷也存在差异（如图1所示）。

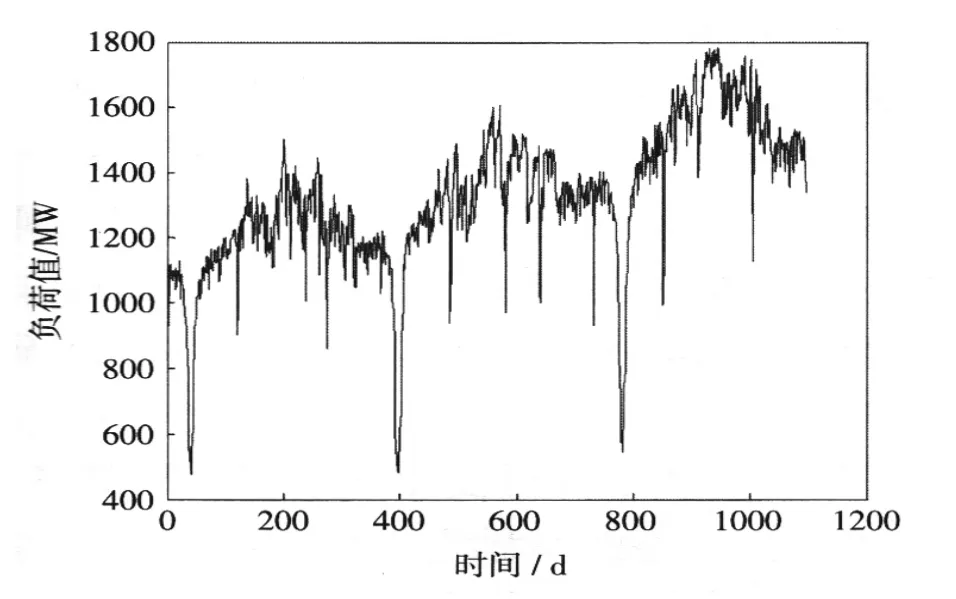
图1 某市连续3年上午8∶00的负荷波动曲线Fig.1Load wave curve at 8∶00 am of one city for three consecutive years

电力负荷模式的这种差异为分区变结构多模型预测提供了可能。对于不同日期同一时间点而言，利用单一的预测方法，可能在某些时间点呈现出拟合不理想、预测精度较差等结果，若根据数据本身存在的特点划分成不同的分区，对不同分区采用不同的模型拟合预测，预测精度将会大大提高。例如，A模型可能在某一分区预测比较准确，而B模型可能在另一分区的预测比较准确。这样通过聚类选用相似度较高的训练样本作为预测输入，分区域应用多个模型，既可以保证数据特征的一致性，又可以更好地反映不同分区各异的负荷变化规律，从而获得更高的预测精度。因此，本文提出一种多模型分区变结构预测方法，其具体流程如图2所示。

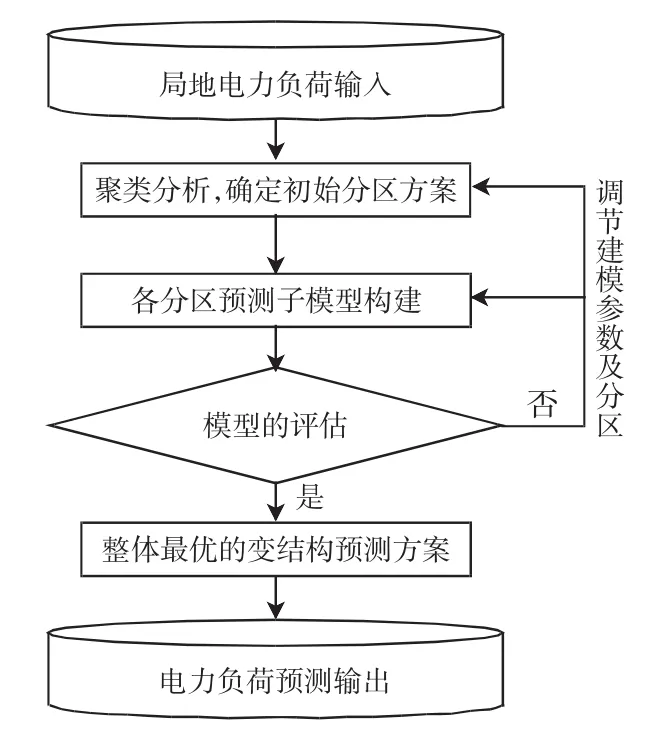
图2 基于支持向量回归的分区变结构负荷预测流程Fig.2Flow chart of variable structure load forecasting based on partitioned support vector regression

1.2 基于模糊C均值聚类的预测时段分区算法

分区时使用的数据包含：（1）被预测点前3个记录时刻点的负荷数据；（2）被预测点的前一日同一时刻及其前后各一个时间点的负荷数据。

选择模糊C均值聚类法FCM（fuzzy C-mean clustering）进行预测时段分区。模糊划分，使得每个给定的数值点用值在0～1间的隶属度uij来确定其属于各个组的程度。FCM把n个向量xi（i=1，2，…，n）分为C个模糊组，求出每组的聚类中心Ci（i= 1，2，…，C），使得非相似性指标的价值函数J（U，C1，2，…，Cc）达到最小。其中

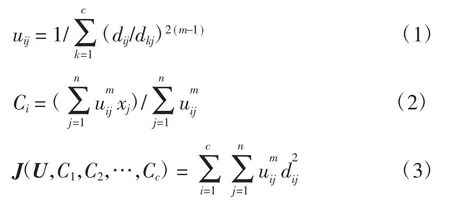
具体算法如下。

步骤1用值在0～1间的随机数初始化隶属矩阵U，使其都满足各列相加等于1；给定聚类数C和初始阈值ε0；

步骤2利用式（2）计算聚类中心Ci（i=1，2，…，C）。

步骤3利用式（3）计算价值函数J（U，C1，C2，…，Cc），如果相对上次价值函数值的改变量ΔJ小于阈值ε0，则算法停止；否则，转步骤4。

步骤4利用式（1）计算新的隶属矩阵U，返回步骤2，直到取到最小的价值函数。

模糊参数m可以取大于等于1的任何值。根据经验，当m=2时，聚类结果最满意，所以在本文实验中取m=2。

1.3 基于支持向量机的各分区预测子模型建立

支持向量机SVM能够实现结构风险最小化，且有较好的泛化能力。目前SVM已经成为计算机学习、模式识别和预测预报等领域的热点技术，并在负荷预测方面取得了很多成功的应用[7～11，16～17]。本文采用SVM方法构建各分区的预测子模型，并选择径向核函数RBF（radial kernel function）函数为SVM的核函数。各子模型具体建立过程如下。

（1）针对给定的分区方案，获取训练数据集

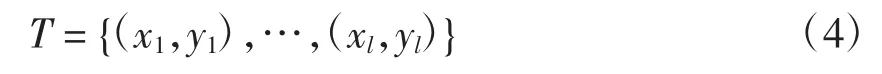
其中：xi∈Rn；yi∈R（i=1，2，…，l）。

（2）选取核函数和SVM参数，求解最优化问题，得解

关于模型参数的确定和优化，给出一种基于仿真评估的确定方法。

1.4 基于预测仿真的模型评估、参数优化和时段分区结构调整

在支持向量回归分析过程中，参数ε取值的变化对模型的预测效果影响不大，故在实验中ε可取为定值0.001。但惩罚参数D和核函数参数σ对模型结构及性能具有重要影响。对于这些参数的取值，本文给出一种基于模型评估的参数确定方法。该方法首先设计系列仿真实验，经训练和测试，得到测试模型的预测结果；然后，根据实验结果评估模型性能的优劣；最后，参考满意度指标选择可行的参数取值。定义衡量满意度的指标为

式中：N为预测点数；Nk（k=1，2，…，s）为测试中误差率小于δ（根据实验δ可做适当调整，本实验中将δ取为2%）的预测点数。

参数选择与时段分区调整的具体算法如下。

步骤1输入参考向量C和m，利用模糊C均值聚类算法进行聚类分析，获取初始分区方案P0。

步骤2给定初始参数范围，D为[10，1 000]，σ为[1，50]，且分别以步长为10和5对分区进行训练与测试，记录输出测试结果中最大误差不超过3%的参数。

步骤3缩小选取的参数范围。缩小D和σ的步长分别为1和0.1进行训练和测试，利用输出结果计算r。若r〉95%，则认为达到满意度，算法合理，输出可行参数；否则扩大参数D的范围为[10，10 000]，转步骤2。

步骤4若调整参数范围后依然达不到满意度，增加聚类数C，转步骤1调整分区方案。

步骤5若上述操作都达不到满意度，则取平均相对误差最小的，输出可行参数D和σ。

步骤6每一分区均重复实验3次，得到可行参数D和σ。

1.5 基于SVR的分区变结构负荷预测算法

在以上讨论的基础上，可给出基于支持向量回归的分区变结构负荷预测算法如下。

步骤1选择特征属性组成局地电力负荷输入数据。

步骤2利用模糊C均值聚类法对输入数据进行聚类分析，得到初始分区方案P0。

步骤3给定初始参数范围，按照各分区预测子模型构建过程建构各分区预测子模型。

步骤4利用参数选择与分区调整策略，适当调整参数取值范围和时段分区结构，给出整体可行的变结构预测方案。

步骤5选择被测数据特征属性组成测试数据，根据与各类中心的距离判断所属分区。

步骤6对局地电力负荷进行预测，给出预测结果。

2 仿真实验分析

2.1 数据选择与实验设计

本文采用某地区2005年1月1日至2007年12月31日之间，每半个小时记录一次当地历史负荷数据，主要针对预测难度较大、精度较低的上午8∶00时负荷进行验证分析。模型的输入向量为各时间点分区的参考向量，模型输出为8∶00的负荷值。这样，模型的输入变量个数为6，由历史数据组成的输入输出样本数据个数为1 087个（剔除部分数据缺失的样本）。由于核函数依赖于输入样本向量的内积，而在本实验中属性的取值范围很大，这样容易造成计算复杂，训练时间较长。为避免以上情况的发生，将属性值归一化为

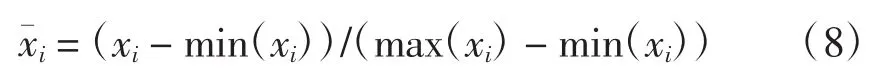
对输入变量进行归一化处理后，先进行分区，然后随机选择训练样本和测试样本，构建各分区子模型。其中训练样本共727个，测试样本共360个。

为了说明该模型的优越性，本文选取神经网络预测方法作为对比方案。选取相对误差（RE）、最小相对误差、平均相对误差为两预测方案的比较参数，其中

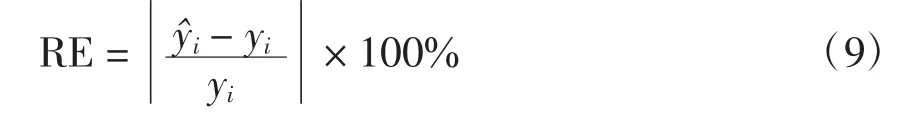
2.2 实验结果及分析

利用本文所述模型对2008年1月1日至2月29日的8∶00（共59个，2月20日实际值缺失，没有给出结果）进行预测。所预测的时期属于节假日较多、波动较大的阶段，而且上午8∶00的负荷值也是预测精度较难把握的一个时间点。利用本文所建立的模型和BP神经网络分别进行预测，结果如图3、图4和表1所示。

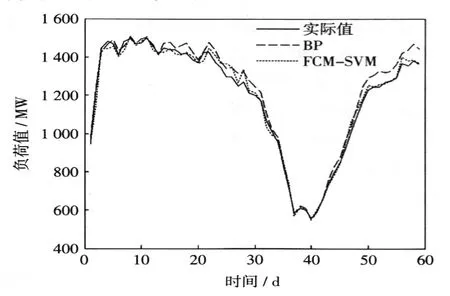
图3 两种方案负荷预测值和实际值曲线Fig.3Actual and forecasting load curves of two methods

由图3可以很显然地看出，基于支持向量回归的分区变结构负荷预测模型所得结果对实际值的拟合，明显优于传统的BP神经网络的拟合效果，尤其是在2月下旬，基于支持向量回归的分区变结构负荷预测模型拟合效果更为明显。误差较大的区段比较集中地出现在1月末2月初，这段时间处于春节前后，影响因素较多，负荷波动较大。该结果可以证明本文所提模型的有效性，以及相似性较高的时段可以采用同一模型预测的构想。

为进一步比较，对两种预测方案的误差范围进行了统计分析，结果如图4所示。

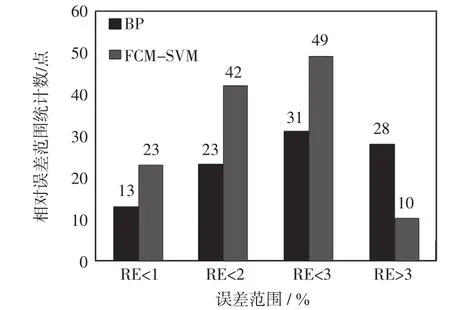
图4 两种方案误差范围比较Fig.4Error range comparison between two methods

从图4可以看出，支持向量回归的分区变结构模型的性能明显优于BP神经网络模型。事实上，以预测结果相对误差不大于3%来衡量，支持向量回归的分区变结构模型有49个点（占预测点总数的83.05%）的相对误差分布在3%以内区域，其中有42个点（占预测点总数的71.19%）分布在小于2%的区域。而BP神经网络模型有接近一半的预测点预测精度都在超过3%的区域，且在每一个误差范围的统计数目，支持向量回归的分区变结构模型都远远大于BP神经网络模型。因此，可以看出本文所建立的模型预测效果较好。

更进一步，表1给出了对两种方案的最小相对误差和平均相对误差的对比结果。

表1 两种预测方案最小相对误差和平均相对误差对比Tab.1Comparison between minimal relative error and average relative error of two methods%

从表1可以看出，FCM-SVM模型的最小相对误差为0.05%，BP神经网络模型为0.15%。可见FCM-SVM模型的最小相对误差预测精度比BP神经网络模型提高了2倍。从平均相对误差来看，FCM-SVM模型和BP神经网络模型预测效果分别为1.70%和2.88%，FCM-SVM模型的预测精度提高了40.97%。

3 结语

本文研究局地电力负荷预测问题，给出一种利用模糊聚类进行预测时段分区，借助支持向量机方法构建时段预测模型的变结构多模型负荷预测方法，建立了一种基于仿真分析的模型评估和优化方法框架，并借助实验分析验证了方法的有效性。

[1]牛东晓，曹树华，卢建昌，等.电力负荷预测技术及其应用[M]．北京：中国电力出版社，2009．

[2]康重庆，夏清，张伯明（Kang Chongqing，Xia Qing，Zhang Boming）.电力系统负荷预测研究综述与发展方向的探讨（Review of power system load forecasting and its development）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（17）：1-11．

[3]Kandil M S，El-Debeiky S M，Hasanien N E.Long-term load forecasting for fast-developing utility using a knowledge-based expert system[J].IEEE Trans on Power Systems，2002，17（2）：491-496．

[4]Ferreira V H，Alves da Silva A P.Toward estimating autonomous neural network-based electric load forecasters [J].IEEE Trans on Power Systems，2007，22（4）：1554-1562．

[5]赵菁，许克明（Zhao Jing，Xu Keming）.神经网络和模糊理论在短期负荷预测中的应用（Application of neural and fuzzy theory in short-term load forecasting）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（3）：129-133.

[6]霍明，罗滇生，何井龙（Huo Ming，Luo Diansheng，He Jinglong）.短期负荷预测中SVM参数选取的混沌优化方法（Chaos optimization method of SVM parameters selection for short-term load forecasting）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（5）：124-128.

[7]陈柔伊，张尧，武志刚，等（Chen Rouyi，Zhang Yao，Wu Zhigang，et al）.改进的模糊聚类算法在负荷预测中的应用（Application of improving fuzzy clustering algorithm to power load forecasting）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（3）：73-77.

[8]Elattar E E，Goulermas J，Wu Q H.Electric load forecasting based on locally weighted support vector regression[J]. IEEE Trans on Systems，Man and Cybernetics，2010，40（4）：438-447．

[9]Sapankevych N，Sankar R.Time series prediction using support vector machines：a survey[J].IEEE Computational Intelligence Magazine，2009，4（2）：24-38．

[10]Wang Jingmin，Zhou Yamin，Chen Xiaoyu.Electricity load forecasting based on support vector machines and simulated annealing particle swarm optimization algorithm[C]// IEEE International Conference on Automation and Logistics.Jinan，China：2007．

[11]Lu Ning，Zhou Jianzhong，He Yaoyao，et al.Simulated annealing theory based particle swarm optimization for support vector machine model in short-term load forecasting [C]//International Conference on Information Engineering and Computer Science.Wuhan，China：2009．

[12]Amjady N，Daraeepour A.Midterm demand prediction of electrical power systems using a new hybrid forecast technique[J].IEEE Trans on Power Systems，2011，26（2）：755-765．

[13]耿伟华，孙衢，张翠霞，等（Geng Weihua，Sun Qu，Zhang Cuixia，et al）.基于改进的模糊神经网络的短期负荷预测（Short-term load forecasting based on improved fuzzy neural network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（5）：29-32.

[14]牛东晓，刘达，陈广娟，等（Niu Dongxiao，Liu Da，Chen Guangjuan，et al）.基于遗传优化的支持向量机小时负荷滚动预测（Support vector machine models optimized by genetic algorithm for hourly load rolling forecasting）[J].电工技术学报（Transactions of China Electrotechnical Society），2007，22（6）：148-153．

[15]王娟，刘明治（Wang Juan，Liu Mingzhi）.蚁群算法滚动优化的LS-SVM预测控制研究（Study of LS-SVM predictive control using ant colony algorithm rolling optimization）[J].控制与决策（Control and Decision），2009，24（7）：1087-1091．

[16]李云飞，黄彦全，蒋功连（Li Yunfei，Huang Yanquan，Jiang Gonglian）.基于PCA-SVM的电力系统短期负荷预测（Short-term load forecasting based on PCA-SVM）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（5）：66-70.

[17]张智晟，马龙，孙雅明（Zhang Zhisheng，Ma Long，Sun Yaming）.混沌理论和支持向量机结合的负荷预测模型（Load forecasting model using chaos theory and support vector machine）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（6）：31-35.

Partitioned Support Vector Regression and Its Application on Load Forecasting

GU Yun-dong，HU Fang-fang
（School of Mathematics and Physics，North China Electric Power University，Beijing 102206，China）

A multi-model based variable structure forecasting method for local short term electric load is proposed based on fuzzy clustering and support vector regression（SVR）.Firstly，the main idea of this method is introduced. Then，prediction time was partitioned into several sections adaptively by means of fuzzy C-means clustering，according to the characteristics of local power load pattern.Sub-models for each section were constructed based on support vector regression in the following.A simulation analysis based model evaluation and optimization method was proposed for the selection of model parameters and the regulation of section structure.The results of contrasting tests show that the proposed method has higher accuracy and stronger robust than neural network.

load forecasting；partitioned support vector regression（PSVR）；fuzzy C-mean clustering（FCM）；adaptive partition；variable structure；model evaluation

TM744

A

1003-8930（2013）03-0020-05

谷云东（1976—），男，副教授，硕士生导师，研究方向为模糊系统建模、评估优化与控制。Email：guyund@126.com

2012-04-18；

2012-05-17

国家自然科学基金项目（71171080）；国家重点基础研究发展计划（973计划）项目（2009CB-320602）；中央高校基本科研业务费专项资金资助项目（12MS84）

胡芳芳（1987—），女，硕士研究生，研究方向为电力系统负荷预测。Email：huff626@163.com