考虑电动汽车充电站选址定容的配电网规划

陈婷，卫志农，吴霜，孙国强，韦延方，许晓慧

（1．河海大学能源与电气学院，南京 210098；2．中国电力科学研究院，南京 210003）

考虑电动汽车充电站选址定容的配电网规划

陈婷1，卫志农1，吴霜1，孙国强1，韦延方1，许晓慧2

（1．河海大学能源与电气学院，南京 210098；2．中国电力科学研究院，南京 210003）

针对电动汽车充电站选址定容的配电网规划问题，建立了以配电网投资及运行成本、电动汽车充电站投资及运行成本最小为优化目标的模型。采用带精英策略的改进树形结构编码单亲遗传算法ITSE-PGA（improved tree structure encoding partheno-genetic algorithm），在配电网规划的同时进行了电动汽车充电站位置和容量的优化。不同于用于传统的配电网规划的树形结构编码单亲遗传算法，该方法在含电动汽车充电站的优化过程中，配电网络不一定连通，所以要对不可行解做特殊处理。通过算例仿真，验证了该方法的可行性和有效性。

电动汽车充电站；配电网规划；单亲遗传算法；树形结构编码

近年来，随着全球环境的日益恶化以及石油资源的日趋紧张，电动汽车作为新型能源交通工具越来越受到关注，其发展前景广阔[1]。充电站、充电桩及电池等充电设施，是发展电动汽车的重要配套基础设施[2，3]。电动汽车充电站的接入将会引起配电网负荷的增长，以及配电网投资与运行成本的提高。为以较低成本满足电动汽车的充电需求，亟需研究考虑充电站位置和容量优化的配电网规划问题[4]。全面地规划优化配电网架结构，能够有效地缩小容量要求、降低网络损耗、减少施工投入，提高电力公司人力物力资源的利用率，有效降低建设投资和维护费用，为国家和电力公司带来可观的经济效益。

目前已有文献对电动汽车充电站的规划问题进行了研究[5～11]。文献[5]提出用2步筛选法来确定充电站的候选站址，构造了电动汽车充电站最优规划的数学模型，并采用改进的原对偶内点法来求解。文献[6]分析了影响电动汽车充电站规划的诸多因素，并就充电站的布局规划问题，提出了应满足充电半径要求，与电动汽车交通密度、充电需求分布、城市总体规划相配合等的原则性建议。文献[7]应用区域交通流量守恒定理，将小区内的电动汽车总量视为充电站的负荷点，在此基础上做出电动汽车的总量和分布预测，提出了充电站的年最小费用模型，并运用遗传算法对实例进行求解。文献[8]运用动态交通网络思想建立了基于硬时间窗约束下的充电站布局及最佳规模确定的多目标优化模型，该模型将充电者充电成本和充电站投资者成本最小化作为优化目标。综上所述，对于电动汽车充电站的选址定容研究，主要考虑了影响充电站本身经济运行的诸多因素，而充电站与配电网结合进行规划的文献目前较少。文献[4]考虑了电动汽车用户的方便性和充电站接入电网的成本，文中提出的辐射状约束可以保证规划方案的辐射状结构。文献[9]针对集中型充电站接入的电网规划问题，综合考虑电力网络和交通网络因素，建立了集中型充电站的定址分容模型。电动汽车充电站作为电网的一部分，它的接入必然对电网的规划造成影响，比如网络投资和网损的增加，线路和变压器过载，带来新的负荷高峰，恶化电能质量等。如何使充电站成本和电网建设及运行成本最小是本文研究的问题。

在配电网规划的求解算法中，简单遗传算法、禁忌搜索、蚁群算法、粒子群算法等随机优化算法在生成个体时会产生大量的不可行解，导致计算速度慢，因此需要构造合理的编码及进化策略，以提高算法效率[12～18]。树形结构编码单亲遗传算法应用于一般的配电网规划中产生的解均是可行解[17]，本文采用改进的树形结构编码单亲遗传算法ITSE-PGA（improved tree structure encoding partheno-genetic algorithm），在配电网规划的同时进行了电动汽车充电站位置和容量的优化，在优化过程中产生的解不全是可行解，但只需在解码过程中做出简单的判断，计算速度快，具有良好的寻优效果。

1 数学模型

1.1 问题描述

本文的研究对象为一个包含供电首端、充电站备选站址节点和传统负荷节点的配电网络。另外为了规划充电站备选站址的容量，本文引入了单位容量节点，使其与所有的充电站备选站址虚拟相连。

1.2 目标函数

以配电网中线路的投资费用f1、运行费用（主要指网损）f2以及电动汽车充电站的投资及运行费用f3总和最小为目标建立模型，其模型为

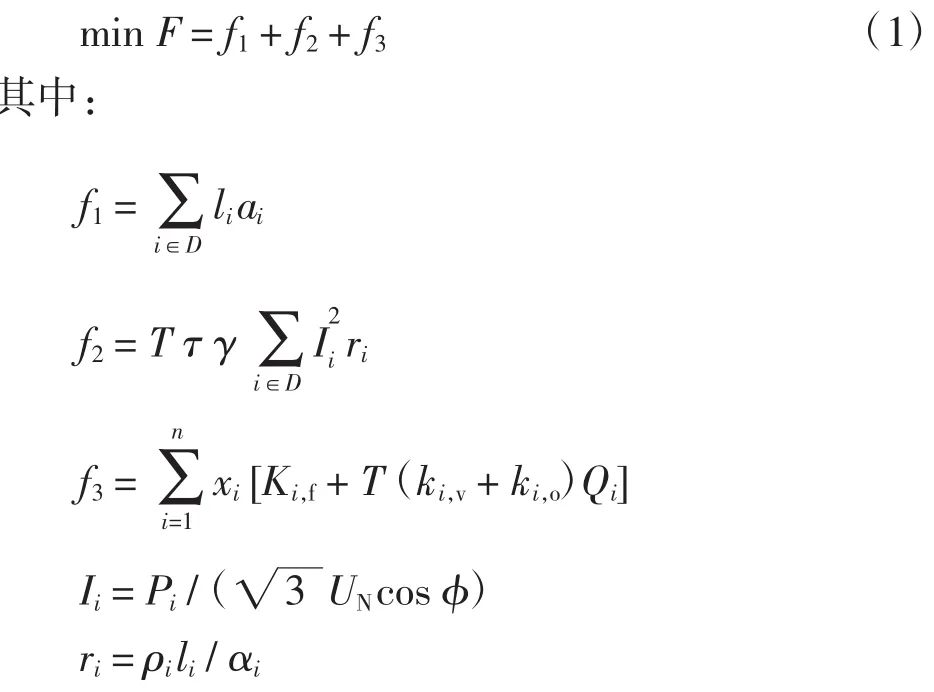
式中：f1为线路投资费用，万元；f2为规划年限内的网络损耗（主要指线损）费用，万元；f3为在规划年限内充电站付出的总成本，万元；D为新建线路集合；li为第i条线路的长度，km；αi为第i条线路单位长度的建设费用，万元/km；T为规划年限，a；τ为年最大负荷利用小时数，h；γ为单位电量的费用系数，元/（kW·h）；Ii为流过第i条线路的电流，A；ri为第i条线路的电阻，Ω；n为充电站备选站址的个数；Ki，f为充电站备选站址i新建的固定成本，万元；xi为充电站i是否建设的二元决策变量，取值为1表示该待选站址将建设充电站，取值为0表示不在该待选站址建设充电站；ki，v为折算到一年，单位容量对应的平均可变投资，万元/MW；ki，o为折算到一年，单位容量对应的平均运行成本，万元/ MW；Qi为充电站备选站址i的容量，MW；Pi为顶点i的年最大负荷平均值，kW；UN为配电网的额定电压，kV；cos φ为功率因数；ρi为电阻率，Ω·mm2/ km；αi为截面积，mm2。

1.3 约束条件

1）辐射状结构和连通性约束

网架结构规划首先要解决的就是网络的连通性和辐射性约束问题，即避免通常所说的“孤岛”与“环岛”情形。

2）功率平衡约束

本文采用直流潮流作为网络功率平衡的约束条件[9]，负荷节点有功功率平衡约束为

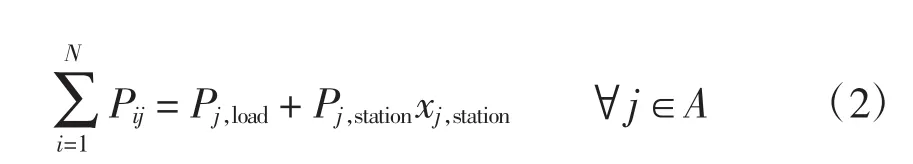
式中：Pij为线路ij的有功传输功率；Pj，load为节点j处除充电站外的负荷；Pj，station为充电站的负荷；xj，station为节点j处是否建设充电站的二元决策变量；A为负荷节点集合；N为网络总结点数。

3）不等式约束

1.4 约束条件的处理

本文辐射性约束自动满足。由于充电站单位容量节点的加入，在随机优化过程中，可能会将充电站单位容量节点当作交叉节点进行规划，从而破坏网络的连通性。本文在编写程序时将此种情况予以排除，保证了网络的连通性。线路功率约束在选线型时加以约束，线路中流过的电流不超过线路能承受的最大电流。

2 树形结构编码单亲遗传算法及其改进

2.1 染色体表达方式

本文中单亲遗传算法采用树形结构编码，将配电网中各负荷点及电源点之间的连接关系和充电站单位容量节点与充电站备选站址节点之间的连接关系用多个树形结构（森林）表示。用一个节点类的对象数组Node代表染色体，采用节点类对象的属性变量保存各节点及其父节点、子节点的编号，据此保存图的树形结构信息。并通过改变各节点的父节点及对应子节点，来达到改变图的拓扑结构的目的。线路的修建与否、充电站单位容量节点与充电站备选站址节点之间连接与否由各节点间是否存在父子关系来决定。若两节点间存在父子关系，则修建对应的线路或连接对应的充电站单位容量节点与充电站节点，否则不修建或不连接。

2.2 单亲遗传操作及其优点

单亲遗传算法PGA（partheno genetic algorithm）与传统遗传算法TGA（traditional genetic algorithm）类似，也是一种采用随机搜索方式的种群算法。其基本原理[17]是：通过遗传算子作用于父代种群，从而产生适应性更强的后代种群；通过反复上述过程，进而达到种群进化的目的。由于本文采用树形结构编码的单亲遗传算法，考虑到改变树的结构所产生的效果主要是改变了某个或某些节点的父节点，故本文的单亲遗传算子采用移位算子和重分配算子[17]。这两种算子的优点在于它们在对个体进行随机优化时不改变网络的辐射性和连通性结构。

2.3 适应度计算

适应度函数由数据模型中的目标函数所决定的，数据优化模型中的目标函数是以经济效益为参考的。在种群产生之后，通过译码操作，将种群中每个个体的染色体转化为可行解对应的数据变量，然后代入求解模型的目标函数中，获得每组解所对应的经济效益。经济效益即为每个个体对应的适应度，经济效益差的个体被淘汰，经济效益好的个体优先生存，通过交叉、变异，最终产生最优解。

算法搜索到的最优解要使目标函数值F尽量小，而适应度作为评价优劣的标准总是寻求最大解，且适应度大于零。因此本文取适应度

式中，M为足够大的常数，以保证适应度恒为正值。

2.4 精英保留策略

精英保留策略是为了解决由于随机因素导致优化过程中优秀个体丢失的问题。算法开始时随机产生一个初始群体A0，在此基础上采用移位、重分配等遗传操作产生一个新群体B0，A0和B0的群体规模均为N。将At和Bt并入到Ct中（初始时t= 0），针对Ct计算所有个体的适应度并从大到小排序，从中选取前N个个体进入At+1，直到t达到最大迭代次数。

2.5 电动汽车充电站位置和容量的优化

文献[17]将树形结构编码单亲遗传算法应用于单一的配电网规划问题中获得了很好的效果。而本文在配电网规划的同时进行电动汽车充电站位置和容量的优化，以期达到两者经济性最佳。因此本文引入充电站单位容量节点（1 MW）虚拟地与各个充电站备选站址节点相连，将充电站单位容量节点当作负荷节点，一起参与网络拓扑的规划。在个体解码时，首先检查是否将充电站单位容量节点当作中间交叉节点规划到网络拓扑中。当单位充电容量节点5同时与充电站备选站址节点3和节点4相连（如图1所示），此为不可行解。从整体看，网络呈辐射连通状，但去除单位充电容量节点，网络不连通，因此排除这一个体。由充电站备选站址节点连接的单位容量节点数，可以知道充电站备选站址节点容量。如图2所示，充电站备选站址3连接了一个单位容量节点5，故充电站备选站址节点容量为1 MW，充电站备选站址4连接了两个单位容量节点6和节点7，故充电站备选站址节点容量为2 MW。然后去除虚拟连接的充电站单位容量节点，计算目标函数以及适应度。将容量规划的连续问题离散化后，采用改进的树形结构编码单亲遗传算法，快速解决了电动汽车充电站选址定容和配电网规划联合优化问题。

图1 不可行解示例Fig.1One example of infeasible solutions

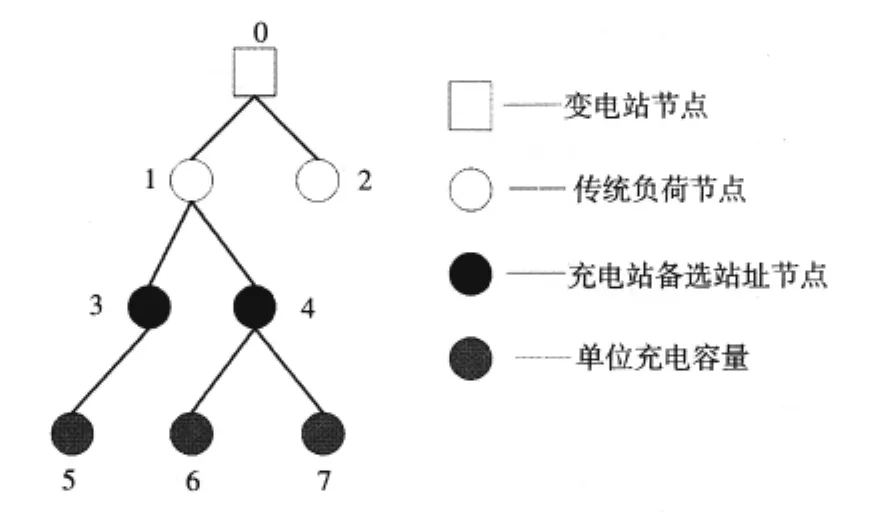
图2 可行解确定容量Fig.2Determining capacity with a feasible solution

2.6 初始方案的产生

本文结合kruskal最小生成树算法产生初始群体，以获得可行（辐射及连通）且相比随机产生的网络较优的初始方案，步骤如下。

步骤1将充电站单位容量节点与充电站备选站址节点之间虚拟支路长度设为一个相同的大值，对所有支路（包括充电站单位容量节点与充电站节点之间虚拟支路）按长度从小到大进行排序，存入一个二维数组Q[n][2]中，Q[i][0]存支路首节点编号，Q[i][1]存支路末节点编号。

步骤2标记各节点标识signal为各节点编号i。

步骤3从Q中取出一条支路加入T[m][2]中，看这条支路的首节点与末节点标识是否相同，如果相同则删除该支路；如果不同，则该边加入T，且遍历已形成的树，将所有与末节点标识相同的节点标识修改为首节点标识。

步骤4检查是否所有的节点都已连接，如果是则遍历整棵树，在Node[]数组中相应对象的属性变量中保存此二节点的父子关系，结束该初始方案，否则转步骤3。

3 算法流程

树形结构编码单亲遗传算法的具体步骤如下：

步骤1产生初始化种群A0，迭代次数t=0；

步骤2解码，适应度值计算，进行个体评价；

步骤3判断t是否大于最大迭代次数，如果是，输出最优解；否则，进入下一步；

步骤4移位、重分配后解码看是否为不可行解，如果是，则去除；否则由充电站备选站址节点连接了几个单位容量节点，则可以知道充电站备选站址节点容量。并计算目标函数以及适应度值。如此循环往复直到得到相应个数的新种群Bt；

步骤5Ct=At∪Bt，针对Ct中的每个个体按适应度值从大到小排序；

步骤6采用精英保留策略，选取前N个个体进入At+1；

步骤7t=t+1，转步骤3。

4 算例分析

算例如图3所示[19]，区域总充电需求为6 MW，数字为各节点编号，充电站备选站址为节点4～6，节点0～9间的虚线为可以架线的走廊，节点4～6与节点10～15间的虚线为虚拟连接的支路，以便确定充电站备选站址节点的容量。表1为网络节点负荷情况，可以架设线路的长度如表2所示，充电站备选站址参数如表3所示，模型求解中采用的单亲遗传操作参数如表4所示。补充如下数据：取单位电量费用系数为0.5元/（kW·h），规划周期为10 a，年最大负荷利用小时数为4 000 h，配电网额定电压为10 kV，各个负荷点的功率因数cos φ为0.85。导线提供LGJ-50，LGJ-70，LGJ-95，LGJ-120，LGJ-150，LGJ-180和LGJ-240等7种型号，且只能单回路架线。

图3 待规划的配电网络Fig.3Initial distribution network to be planned

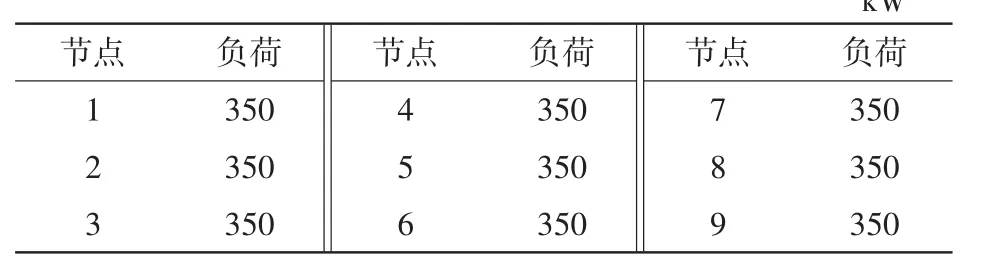
表1 网络节点负荷Tab.1Loads of network nodes

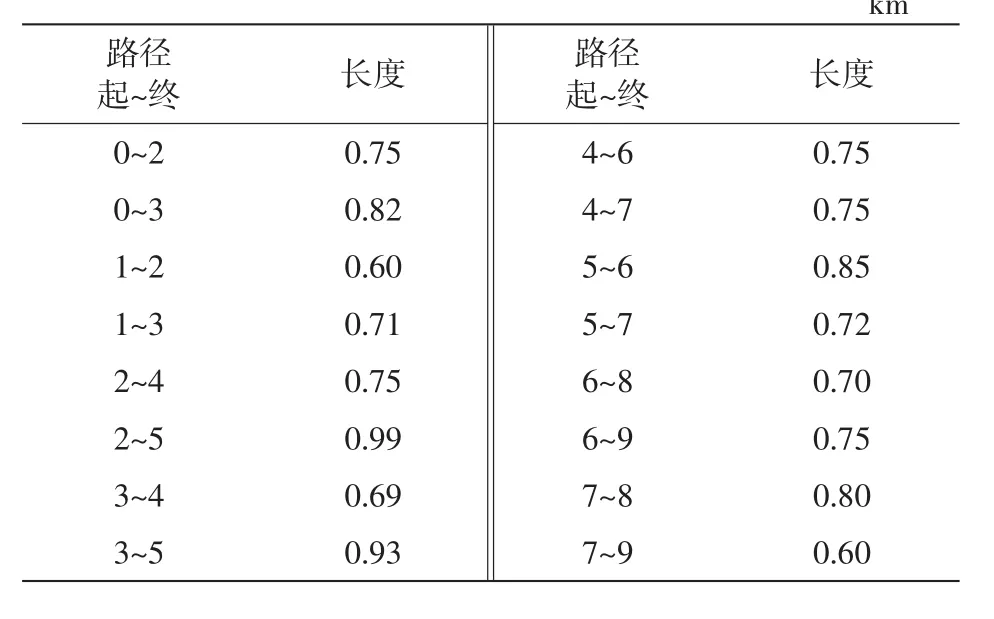
表2 线路长度Tab.2Length of the line

表3 充电站备选站址参数Tab.3Parameters of alternative sites for charging station

表4 单亲遗传算法的操作参数Tab.4Operation parameters of PGA

分2种方案进行优化规划计算。方案1采用表3的参数计算，方案2将充电站备选站址节点4～6的容量设为固定值，分别为2、1、3MW。

在Visual C++环境下，在CPU主频2.00 GHz、操作系统为Windows XP的计算机上上述算例的计算时间均不到1s。

图4为方案1（即本文算法）的规划结果，其中表5为方案1网架规划结果，表6为方案1的充电站定址分容结果。利用改进的树形结构编码单亲遗传算法得出最佳个体生成代数为16，最小费用为1 338.617万元。

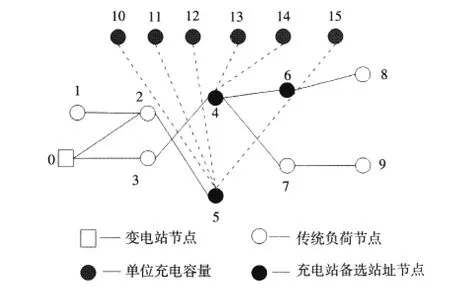
图4 方案1规划结果Fig.4Planning results of scheme 1

图5 方案2规划结果Fig.5Planning results of scheme 2

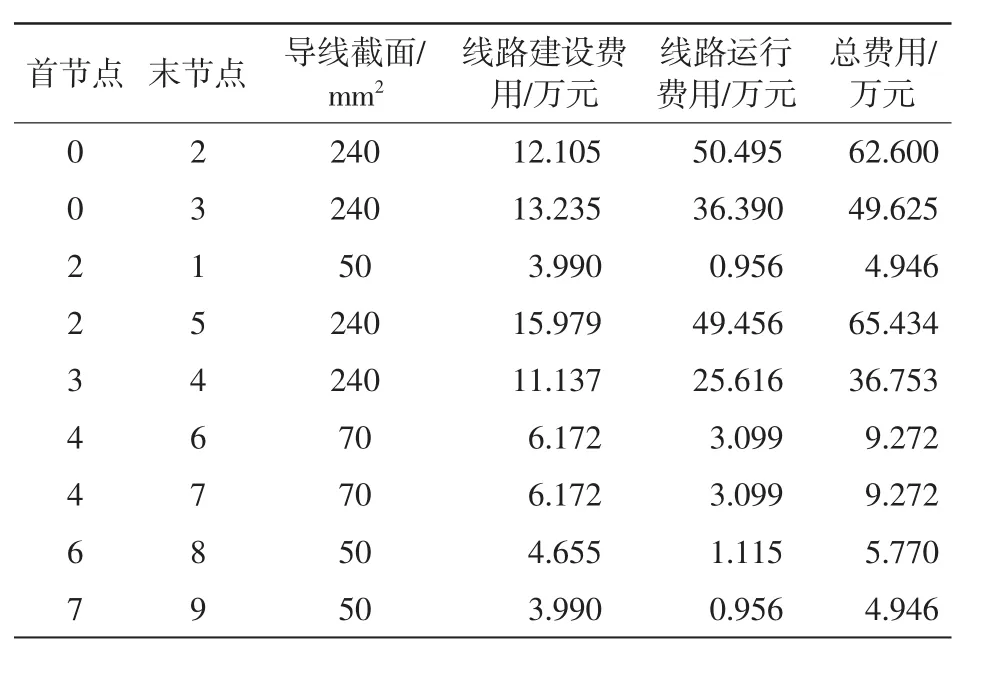
表5 方案1网架规划结果Tab.5 Results of distributionnet work planning of scheme1

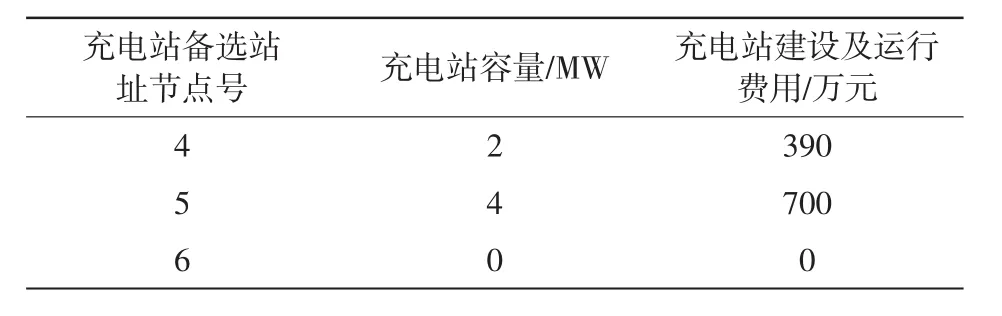
表6 方案1充电站定址分容结果Tab.6 Results of site and capacity of stations of scheme 1

表7 方案2网架规划结果Tab.7 Results of distribution net work planning of scheme2

表8 方案2充电站定址分容结果Tab.8 Results of site and capacity of stations of scheme 2

表92 种方案的成本比较Tab.9Cost comparison between two schemes

图5为方案2的规划结果，其中表7为方案2网架规划结果，表8为方案2的充电站定址分容结果。最小费用为1 482.481万元。

方案2指定各充电站备选站址的容量，而方案1利用改进的树形结构编码单亲遗传算法将电动汽车充电站的选址和定容考虑在配电网规划模型中。由表9可知，方案1的规划结果比方案2的规划方案节省了大约10%的总成本。由规划结果对比可知，将电动汽车充电站的选址和定容考虑到配电网优化模型中可有效减少包含充电站在内的配电网的总投资与运行成本。

本文提出的改进树形结构编码单亲遗传算法应用于配电网规划和电动汽车充电站定址分容的综合，不仅有效地解决了问题，而且能快速找到最优解，计算速度快。

5 结语

本文将改进的树形结构编码单亲遗传算法应用于配电网规划和电动汽车充电站定址分容，有效地解决了电动汽车充电站接入电网的规划问题。该算法在优化过程中配电网络始终自然呈辐射状，无需辐射性检验，提高了求解问题的效率。然而，由于树形结构编码的特殊性，电动汽车充电站容量优化这一连续性问题被离散化，因此，若要得到更精确的结果，所取单位容量需更为缩小。本文中，单位容量取1 MW，所得解为相对最优解。若将单位容量取为0.1 MW甚至更小，这样从理论上来说可提高求解的精度，然而因为大大增大了解空间，对于随机优化的智能算法而言，要想得到最优解将需要比较多的迭代次数，也可能陷入局部最优，所以选取合适的单位容量是比较重要的。

[1]Parks K，Denholm P，Markel T.Costs and emissions associated with plug-in hybrid electric vehicle charging in the Xcel energy Colorado service territory[EB/OL].http：// www.nrel.gov/vehiclesandfuels/pdfs/41410.pdf，2007.

[2]吴春阳，黎灿兵，杜力，等（Wu Chunyang，Li Canbing，Du Li，et al）.电动汽车充电设施规划方法（A method for electric vehicle charging infrastructure planning）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（24）：36-39，45．

[3]陈加盛，张建华，林建业，等（Chen Jiasheng，Zhang Jianhua，Lin Jianye，et al）.以降低电网损耗为目标的电动汽车充电策略（Strategies for electric vehicle charging with aiming at reducing network losses）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（3）：139-144．

[4]杜爱虎，胡泽春，宋永华，等（Du Aihui，Hu Zechun，Song Yonghua，et al）.考虑电动汽车充电站布局优化的配电网规划（Distribution network planning considering layout optimization of electric vehicle charging stations）[J].电网技术（Power System Technology），2011，35（11）：35-42．

[5]刘志鹏，文福栓，薛禹胜，等（Liu Zhipeng，Wen Fushuan，Xue Yusheng，et al）.电动汽车充电站的最优选址和定容（Optimal siting and sizing of electric vehicle charging stations）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（3）：54-59．

[6]徐凡，俞国勤，顾临峰，等（Xu Fan，Yu Guoqin，Gu Lin－feng，et al）.电动汽车充电站布局规划浅析（Tentative analysis of layout of electrical vehicle charging stations）[J].华东电力（East China Electric Power），2009，37（10）：1678-1682．

[7]李菱，李燕青，姚玉海，等（Li Ling，Li Yanqing，Yao Yuhai，et al）.基于遗传算法的电动汽车充电站的布局规划（Layout planning of electric vehicle charging stations based on genetic algorithm）[J].华东电力（East China Electric Power），2011，39（6）：1004-1006．

[8]任玉珑，史乐峰，张谦，等（Ren Yulong，Shi Lefeng，Zhang Qian，et al）.电动汽车充电站最优分布和规模研究（Optimal distribution and scale of charging stations for electric vehicles）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（14）：53-57．

[9]高赐威，张亮，薛飞，等（Gao Ciwei，Zhang Liang，Xue Fei，et al）.考虑集中型充电站定址分容的电网规划研究（Grid planning considering capacity and site of largescale centralized charging stations）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（7）：40-46．

[10]卢艳霞，张秀敏，蒲孝文（Lu Yanxia，Zhang Xiumin，Pu Xiaowen）.电动汽车充电站谐波分析（Harmonic study of electric vehicle chargers）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（3）：51-54．

[11]Wang Hengsong，Huang Qi，Zhang Changhua，et al.A novel approach for the layout of electric vehicle charging station[C]//International Conference on Apperceiving Computing and Intelligence Analysis.Chengdu，China：2010．

[12]孔涛，程浩忠，李钢，等（Kong Tao，Cheng Haozhong，Li Gang，et al）.配电网规划研究综述（Review of power distribution network planning）[J].电网技术（Power System Technology），2009，33（19）：92-99．

[13]王雷，顾洁（Wang Lei，Gu Jie）.中压配电网优化规划的改进单亲遗传算法（Improved partheno-genetic algorithm for medium voltage distribution network optimal planning）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（3）：72-76．

[14]陈根军，李继洸，王磊，等（Chen Genjun，Li Jiguang，Wang Lei，et al）.基于Tabu搜索的配电网络规划（Distribution system planning by Tabu search approach）[J].电力系统自动化（Automation of Electric Power Systems），2001，25（7）：40-44．

[15]王志刚，杨丽徙，陈根永（Wang Zhigang，Yang Lixi，Chen Genyong）.基于蚁群算法的配电网网架优化规划方法（Ant colony algorithm for distribution network planning）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2002，14（6）：73-76．

[16]张宪，宛津莎，杨薛明，等（Zhang Xian，Yuan Jinsha，Yang Xueming，et al）.基于粒子群算法的配电网网架规划（Distribution network planning based on particle swarm optimization）[J].华北电力大学学报（Journal of North China Electric Power University），2006，33（3）：14-17．

[17]章文俊，程浩忠，王一，等（Zhang Wenjun，Cheng Haozhong，Wang Yi，et al）.基于树形结构编码单亲遗传算法的配电网优化规划（Distribution network optimal planning based on tree structure encoding partheno-genetic algorithm）[J].电工技术学报（Transactions of China Electrotechnical Society），2009，24（5）：154-160．

[18]Jonnavithula S，Billinton R.Minimum cost analysis of feeder routing in distribution system planning[J].IEEE Trans on Power Delivery，1996，11（4）：1935-1940．

[19]戈东方，钟大文.电力工程电气设计手册[M].北京：中国电力出版社，1989．

Distribution Network Planning by Considering Siting and Sizing of Electric Vehicle Charging Stations

CHEN Ting1，WEI Zhi-nong1，WU Shuang1，SUN Guo-qiang1，WEI Yan-fang1，XU Xiao-hui2
（1．College of Energy and Electrical Engineering，Hohai University，Nanjing 210098，China；
2．China Electric Power Research Institute（Nanjing），Nanjing 210003，China）

The problem of distribution network planning by considering siting and sizing of electric vehicle charging stations has recently

the increasing research attention.In this paper，an optimal model is proposed，which aims to minimize the investment and operation costs of the distribution network and electric vehicle charging stations. By using the improved tree structure encoding partheno-genetic algorithm（ITSE-PGA）with elitist strategy，the problems of distribution network planning and optimization of the location and capacity of electric vehicle charging stations can be tackled simultaneously.Different from the ITSE-PGA for traditional distribution network planning，the considered distribution network here is not necessarily connected in the optimization process when considering electric vehicle charging stations，so the infeasible solutions should be specially handled.Finally，simulation results are provided to show the feasibility and effectiveness of the proposed method.

electric vehicle charging station；distribution network planning；partheno-genetic algorithm；tree structure encoding

TM71

A

1003-8930（2013）03-0001-07

陈婷（1989—），女，硕士研究生，研究方向为配电网规划、电动汽车。Email：ctjr@163.com

2012-11-29；

2013-01-14

国家自然科学基金项目（51277052，51107032，61104045）；国网公司总部科技项目：智能配用电的技术体系及仿真基础性问题研究

卫志农（1962—），男，教授，博士生导师，研究方向为电力系统运行分析与控制、输配电系统自动化等。Email：wzn_nj@263.net

吴霜（1989—），女，硕士研究生，研究方向为配电网规划与自动化。Email：wushuanghehai@sina.com