基于遗传算法的弹道优化算法

张乐蓉，宋 龙，章惠君

(中国空空导弹研究院，河南 洛阳 471009)

空空导弹弹道优化研究的目的是提高导弹的飞行性能，达到精确、有效的拦截目标。导弹弹道优化问题已成为现代导弹技术的重点发展方向之一，很多学者在弹道优化方面做了大量研究。文献［1］利用序列二次规划法对导弹纵向弹道整体进行优化，文献［2］通过非线性规划的直接方法优化得到最优的初始弹道等。

但在弹道优化问题中大多数解决方法是数值优化的方法，数值优化本质是根据初始条件，终端约束，指标函数可得到特征弹道，即飞行弹道的基本几何形状，故采用一般数值的方法进行优化在很大程度上受初始条件的约束和影响，尤其是当目标有多个极值点时［1］。而遗传算法是一种模拟物种生存进化体制的搜索算法，它并不依赖于问题本身，通过对种群方向性的选择、交叉和复制操作来完成搜索，同时又具有鲁棒性、隐含并行性等的特点，因而该算法成功的运用于许多复杂优化问题的求解。针对空空导弹的数学模型，对给定的模型及气动参数，将弹道倾角作为控制变量，采用遗传算法优化采样点数据求得优化弹道方案。与比例导引方案弹道相比，在相同时间和相同射程的情况下，遗传算法优化弹道的末端速度较大，具有一定优越性。

1 导弹模型

1.1 导弹模型

不考虑地球自转影响，导弹在铅锤平面内运动的质心运动方程组为

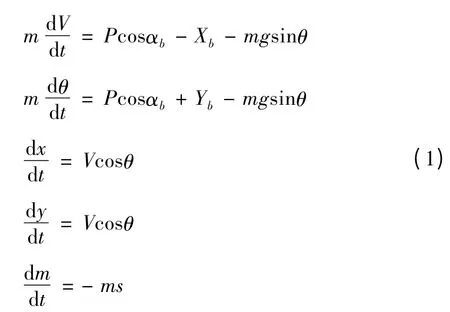
其中m 为导弹质量，P 为发动机推力，X 为阻力，θ 为弹道倾角，Y 为升力，ms 为导弹质量变化率，α 为攻角，V 为导弹速度。

阻力模型:

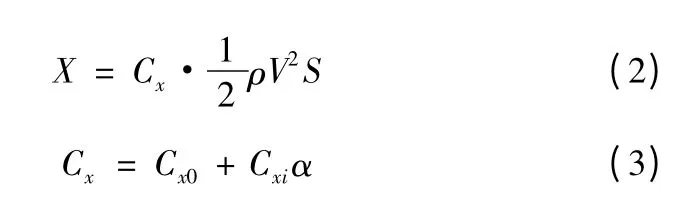
式(3)中，Cx0为零升阻力系数;Cxi为诱导阻力系数。

大气密度模型:

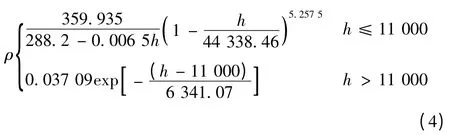
推力模型为:

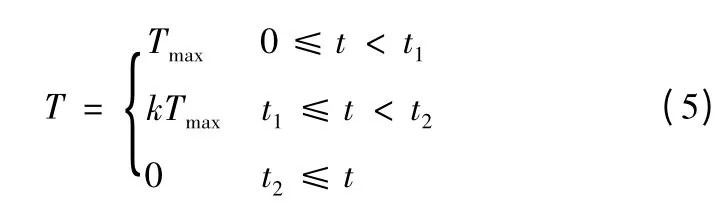
式(5)中，Tmax为发动机所能提供的最大推力;k 为常系数，k∈［0，1］。

1.2 问题描述

本文以末端速度最大值作为性能指标

初始投放条件

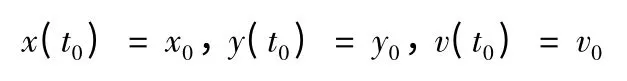
由上可知目标问题为:从已知初始状态(x0，y0，v0)，要求转移到末端时刻t=tf时，脱靶量r≤25 m，v(tf)达到最大。

当导弹模型以及气动力参数都给定时，在给定时间，给定距离的情况下，假定导弹小攻角飞行，则应存在一组优化的弹道倾角，使得导弹能以最大末速度击中目标。而本文就通过寻找这一组优化的弹道倾角从而得到末端速度最大的优化弹道。

2 遗传算法

弹道优化是一种复杂的非线性的多约束(多为隐性约束)问题，现有的传统优化方法均属于局部优化方法，如果目标问题存在多个极值点，通过传统方法是很难得到最优解，因而采用传统优化方法进行弹道优化存在一定的局限性。

遗传算法是一种模拟生物种群进化过程的搜索方法，通过基因编码和种群进化讲复杂的问题简单化，在遗传进化过程中寻找到最优解。遗传算法优化的重点在于基因的编码方式与适应度函数的选取，对优化问题的具体细节要求并不高，因而具有很强的鲁棒性。其寻优是有指导而非盲目的进行搜索，迭代产生的新一代个体总是优越于上一代个体，全局搜索的同时隐含并行性，多点同时进行搜索，使得寻优效率更高。这些优点使得遗传算法对导弹的弹道优化这个复杂的非线性优化问题具有一定的优越性。

3 优化算法设计

3.1 遗传算法方案

3.1.1 编码方案

按照遗传算法优化的设计思想，建立目标优化问题和基因结构之间的关系式遗传算法的关键，即确定算法的编码方式以及解码运算。常用的编码方式有两种:二进制编码与浮点数编码。二进制编码采用固定长度的二进制符号串来表示群体中的个体，其等位基因由{0，1}构成;而所谓浮点数编码则是指个体的每个基因用某一范围内的一个浮点数来表示，这种编码方式直接使用变量的真实值，故不需要解码操作［6］。文中优化的变量为弹道倾角，范围为［0，pi/2］，因而采用二进制编码方式即可满足需求。

3.1.2 基本遗传操作

在遗传算法的进化过程中，起到最关键作用的是选择、交叉和变异操作。因而产生了3 个最基本的遗传操作算子:选择算子、交叉算子和变异算子。通过这3 个算子对进化过程随即性的操作，使得群体在进行n 代后更接近最优解，其接近程度与3 种算子采取的操作形式紧密相关。

1)选择算子。选择算子，也叫做复制算子，它以适应度作为评价的基准，将上一代优秀的个体基因复制遗传到下一代，产生新的群体，使得个体向最优解逐渐靠拢。选择算子是遗传进化过程中的重要环节，其好坏直接影响到算法的优劣。

目前现有的选择算子主要有轮盘赌选择、随机竞争选择、最佳保留选择、确定性选择和无回放随机选择等。

本文采用了最佳保留选择，利用“排名”的思想，从种群众随机的选取K 个个体，然后将这K 个个体按照适应度值得大小进行排序，找出K 个个体中的最优个体，遗传到下一代。

2)交叉算子。在优化过程中，种群是通过基因的交叉操作产生新的个体，从而保证种群的多样性，扩大优化进程寻优的范围。交叉算子直接决定了算法是否收敛，是遗传优化算法的核心操作。

常用的交叉算子有单点交叉、两点交叉、均匀交叉以及算术交叉等。文中采用了两点交叉，使得遗传算法的寻优范围更广搜索能力更强。

3)变异算子。变异操作是模仿生物遗传进化过程中出现的基因突变现象，某些基因位发生突变，产生新的个体，引进变异操作的目的是为了保证种群的多样性，同时使得遗传算法也有了一定的随机搜索能力，防止算法出现早熟收敛。

常见的变异算子有基本位变异、有效基因突变、概率自调整突变、均匀突变以及非均匀突变等。文中采用的是均匀突变，即每一个基因位都以相同概率变动。

3.1.3 适应度函数的选取

适应度是遗传算法用来衡量个体好坏的标准，是寻优过程的评价机制。在每次迭代产生的群体中，适应度高的个体更容易进入下一代，而适应度低的个体进入下一代的几率则相对较低。描述适应度大小的函数则成为适应度函数，指导着遗传优化过程的方向。

文中讨论的导弹最优控制问题以最大末端速度为性能指标，因此这里以末端速度值作为适应度函数。

3.2 算法流程

选用上面介绍的二进制编码方案，选择、交叉和变异算子以及适应度函数构成求解导弹最优化问题的遗传算法，算法流程如图1 所示。

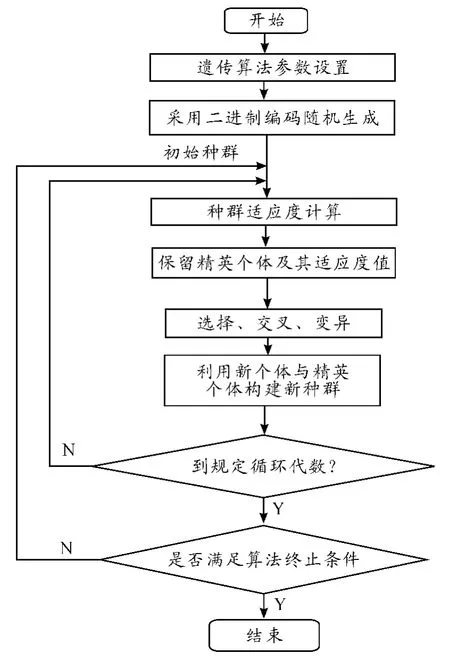
图1 遗传算法设计流程

4 优化算例

给定导弹初始高度为5 000 m，初始速度为300 m/s，目标初始位置为(30 000，5 000)，并以100 m/s 的速度水平向右运动。性能指标是末端速度最大。其他仿真参数如下:

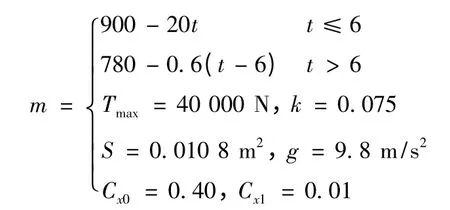
遗传算法种群大小取100，精英个体数目为20，最大迭代次数为100，种群个体范围为［-1.57，1.57］。

利用如上参数采用比例导引仿真得到的弹道，弹道射程为40 km，其末端速度为698.2 m/s，飞行时间为97 s，脱靶量为0。按照根据图1 所示算法，选取20 组采样点数据作为优化变量，利用遗传算法进行计算，在进化100 代后得到了相同飞行时间、射程下的末速度最大弹道，优化得到的弹道的末端速度为730.95 m/s，脱靶量为0.024 0，相比比例导引末端速度是它的1.05 倍。两种方案均用97 s 的飞行时间在(40 000，5 000)点处击中目标，其弹道倾角随时间变化曲线、速度随时间变化曲线以及弹道曲线如图2 ～4 所示。

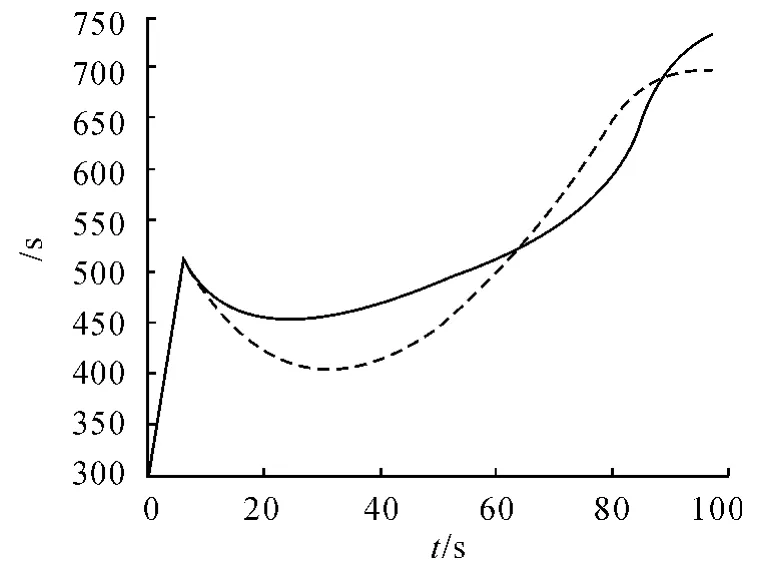
图2 导弹速度随时间变化曲线

图3 弹道倾角随时间变化曲线

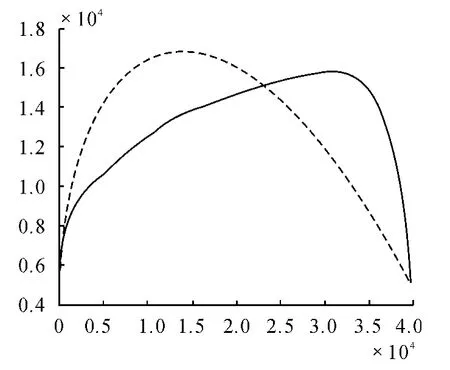
图4 导弹轨迹曲线

5 结束语

遗传算法优化飞行方案先斜向上飞行，然后在下滑段减小导弹轨迹与重力方向的夹角，利用重力和推力的作用来增加优化弹道末段速度，这种飞行方案在同等飞行时间、同等射程情况下，得到的末端速度远大于比例导引飞行方案得到的末端速度。通过比较比例导引方案与遗传优化方案的仿真结果，可以发现基于遗传算法的优化飞行方案在弹道优化方面有一定优越性，为空空导弹标准弹道的设计提供了一种参考。

［1］赵昕，艾飞.地理约束下远程滑翔导弹弹道优化［J］.战术导弹技，2010，6:8-12.

［2］陈罗婧，刘莉，于剑桥.三点法导引导弹初始段弧形弹道优化设计及实现［J］.弹道学报，2009，6:65-69.

［3］熊西军.基于遗传算法的超远程制导火箭弹弹道优化设计［D］.成都:电子科技大学，2009.

［4］耿丽娜，郑志强.基于遗传算法的制导炸弹最优控制律［J］. 中 南 大 学 学 报: 自 然 科 学 版，2007，38（1）: 176-181.

［5］鲜勇，许立军.遗传算法在导弹飞行程序设计中的应用研究［J］.系统仿真学报，2009，21（5）:1502-1504.

［6］肖伟.遗传算法的研究及其在倒立摆中的应用［D］.长沙:中南大学，2011.