伪随机码近炸引信的模糊函数

李红英，杜 军，杨金刚，刘芒龙，王晓霞

(西安机电信息技术研究所，西安 710065)

由于伪码体制引信具有良好的抗干扰性能和距离分辨能力，现已成为引信重要的发展方向之一。国外的“海响尾蛇”导弹便采用伪随机码和脉冲复合调制引信。而国内有关单位伪码引信的研制工作，如文献［1］研究的脉间伪随机二相码脉冲串引信、随机脉位调制与随机二相码调相脉冲串引信。国内在伪码体制引信研制方面已取得很多成绩，对伪码体制引信抗干扰和距离分辨能力的研究，目前大多从伪随机码的相位调制与脉位调制定性描述，推导过程复杂，针对此问题，本文从模糊函数的角度分析了伪随机码近炸引信抗干扰和距离分辨力。

1 伪码近炸引信和模糊函数理论

1.1 伪码近炸引信

伪码体制近炸引信的原理框图如图1 所示，系统主要由发射系统、接收系统、信号处理电路系统与执行机构组成。

图1 伪码体制近炸引信的原理框图

伪码信号由伪码发生器产生，经调制和载波作用后已调信号由天线向外辐射，被目标反射回来的信号由接收天线接收，该信号经过放大、限幅后与伪码延迟器的输出作相关处理。同时按照一定的目标信号识别准则，完成对目标方位的判别。最终根据弹目交会角、交会速度等信息及引战配合的要求，输出启动信号触发执行级产生引爆信号。

1.2 伪码近炸引信工作原理

伪码近炸引信定距原理主要利用收发信号波形的相关性上。伪码探测技术一般要求在引信作用区域的中点处使回码与本地码重合，即此处将出现相关函数峰值。对于一个码元而言，当本地码的前沿与回码的后沿重合时，探测到的最小距离为0;当本地码的后沿与回码的前沿重合时，探测到的最大距离为R，两者之间的状态对应0 ～R 之间的某一距离。

相关器输出归一化幅度与距离延时的关系曲线如图2所示。

图2 相关器输出的归一化幅度与距离延时的关系曲线

图2 中τmin-τmax为引信的预定作用距离区，τ0为作用距离区的中点，此处假设本地码与回码重合，本地码延迟时间τ0等于一个码元宽度(TL);e 为在引信预定作用距离区内所允许的相关器输出幅度下降的大小。显然，近炸引信的距离截止特性、作用距离与引信工作的安全高度都由TL决定。

据图2 得伪码近炸引信作用距离区(ΔR)

由式(1)可知，在所允许的相关度e 一定时，TL越小，ΔR越小。同时，从图2 可见，若TL越大，相关器输出幅度的斜率越小，所对应的截止距离将增大，这样不利于对干扰信号的限制。所以TL应根据引信截止距离和预定作用距离区域的大小综合考虑。

伪码体制引信的发射信号具有多种形式［1-5］，本文为与相位调制与脉位调制研究的结果作对比，采用文献［3］中所提及的发射信号，其数学表示式统一表示为

式中:μ(t)为为单位脉冲;Ci为幅值;Tc为码元宽度;Tp为子脉冲宽度;Tr1为子脉冲重复周期;Tr2为脉冲重复周期。

1.3 模糊函数

模糊函数最初是在研究雷达分辨力问题时提出的，它主要研究2 个不同距离和不同径向速度目标的分辨度。信号s(t)模糊函数定义为其二维互相关函数的模的平方χ，其表达式为

式中τ 与fd分别表示信号的时延和频移，式(3)是模糊函数的一种表达形式，为了计算与分析方便，模糊函数还可写为卷积的形式，即

为方便仿真程序按式(4)计算信号的模糊函数。

2 伪码近炸引信的模糊函数

根据函数定义式(2)～式(4)，可推导出伪码近炸引信的平均模糊函数，由于篇幅有限，这里不再写出推导过程，直接给出结果

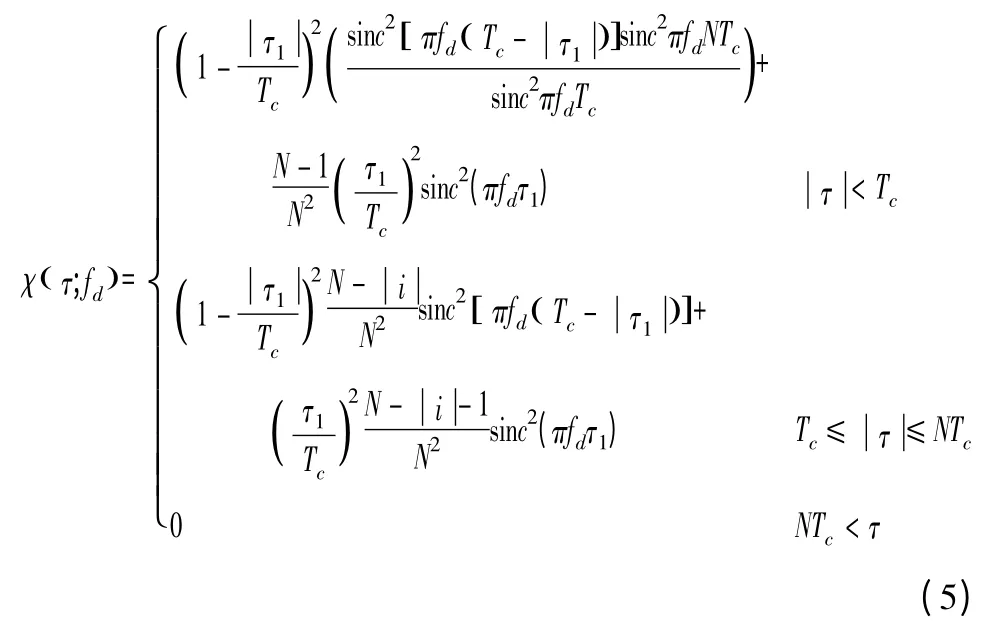
式中令τ=iTc+τ1，i 为整数。若令平均模糊函数中τ=0，则得到速度模糊函数为

若令平均模糊函数中fd=0，则得到距离模糊函数为

模糊函数式(5)～式(7)描述了目标的距离/多普勒平移产生的影响，它可以用来分析波形的一些特征，如目标的距离分别能力，以及对杂波的影响等。

3 以模糊函数对伪码近炸引信仿真与分析

伪码近炸引信信号平均模糊函数与波形观察时间NTc和码元宽度Tc有关，选择参数Tc=0.012 5 μs，参数N 变化时对平均模糊函数、速度模糊函数和距离模糊函数进行仿真与分析。

3.1 平均模糊函数仿真与分析

根据式(4)与式(5)及参数N 变化对应的如图3 ～图5所示。

图3 N=8 时的模糊图

图4 N=10 时的模糊图

图5 N=14 时的模糊图

从图3 ～图5 可以看到，伪码近炸引信这种体制，很好消除了距离模糊，当N(脉冲积累数)较小时，较强的副瓣在距离和多普勒轴上都有，若N 较大时，旁瓣在距离轴上很低，而且在多普勒轴上已经不存在明显副瓣，近视为图钉形，说明它有很好的抗干扰性。

3.2 速度模糊函数仿真与分析

根据式(4)～式(6)及参数N 变化时速度模糊函数的影响如图6 ～图8 所示。

明显看出，N 取值越大，主瓣宽度越窄，分辨力越好。在实际的情况下，码元宽度Tc是一定的，则就应该加大脉冲积累数N 的值，即观察信号的时间T =NTc，加长，但N 值过大就会使信号发射后易被截获.使其抗干扰能力下降。

图6 N=8 时速度模糊图

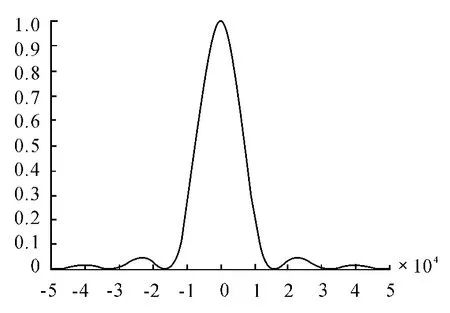
图7 N=10 时的速度模糊图

图8 N=14 时速度模糊图

3.3 距离模糊函数仿真与分析

根据式(4)～式(7)及参数N =8，Tc=0.012 5 μs 得到伪码信号的波形距离模糊图，如图9 所示。

图9 伪码近炸引信信号的波形距离模糊图

4 结束语

本文提出了伪码引信的模糊函数。利用模糊函数对伪码引信信号进行分析，并对平均模糊函数图、速度模糊函数图、距离模糊函数图进行了仿真验证，结果表明，伪码近炸引信具有很好的抗干扰性能和距离分辨力，这与伪码的相位调制和脉位调制研究的结果相同。模糊函数的图钉这一性质有助于伪码近炸引信信号的波形设计，同时为分析伪码近炸引信信号提供了另一种方法。

［1］朱晓华. 脉位调制脉冲串雷达信号理论与应用研究［M］.南京:南京理工大学，2002:7-56.

［2］刘已斌，王李军，赵惠昌.伪码体制引信的抗噪声调频干扰性能分析［J］. 电子信息学报，2004，26（12）: 1925-1932.

［3］曹成茂，张河.伪随机码在近炸引信设计中的应用［J］.弹箭与制导学报，2004，24（4）:342-345.

［4］熊刚，杨小牛，赵惠昌.伪随机码调制脉冲串引信及其抗噪声性能分析［J］. 弹箭与制导学报，2006，26（1）:469-473.

［5］黄光明，赵惠昌.伪随机码调相引信的抗干扰与干扰研究［J］.兵工学报，2004，25（6）:684-688.

［6］刘已斌，赵惠昌.PPM 伪随机码及其应用［J］.现代雷达，2004，26（2）:23-26.

［7］Dr.Ing. Petr Bezucha. Mean acquisition times of serial spread spectrum PN acquisition system in the presence of code Doppler［C］//IEEE 7 Int. Sym. On. Spread—Spectrum Tech.App. Prague:［s.n.］，2002:750-755.

［8］姜丹.信息论与编码［M］.合肥:中国科学技术大学出版社，2009:118-153.

［9］宋耀良.随机多元码PPM 脉冲序列及其平均模糊函数［J］.现代雷达，2001（1）:43-47.

［10］张居正.伪随机码调相引信原理与设计［J］.制导与引信，2000（3）:1-7.

［11］胡辉，袁媛. GPS 现代化L5 信号分析［J］. 重庆理工大学学报:自然科学版，2012（3）:93-98.

［12］熊波，秦钊，路明，等.伪码调相脉冲信号识别［J］.四川兵工学报，2011（9）:73-74.