基于卡尔曼滤波最大似然参数估计的气动参数辨识

李正楠，汪 沛，李国辉，李立新

(空军航空大学 a.军事仿真技术研究所;b.模拟训练中心，长春 130022)

飞行器的参数辨识是根据飞行器的输入及其响应确定出飞机的模型和模型中的各个参数数值。随着现代控制理论、统计数学和电子计算机的迅速发展，飞行器气动参数辨识在飞行试验数据分析中的应用得到了飞跃发展，并在飞行器设计、飞行模拟仿真中起着越来越重要的作用。它可以验证和校正飞行器气动力系数的风涧试验和理论分析结果，为地面和空中仿真系统提供正确的飞行力学模型，为飞行器控制系统的设计和改进提供基本数据，还可以鉴定飞行品质，研究高性能飞行器的飞行品质，进行飞行器失事事故分析。本文将卡尔曼滤波融合于最大似然参数估计中，利用最大似然函数渐进一致性、估计的无偏性、良好的收敛特性的特点，对各实际工作点的气动参数进行辨识。

1 基于卡尔曼滤波最大似然参数估计原理

动力学系统的非线性运动方程组可写成下列通用形式:

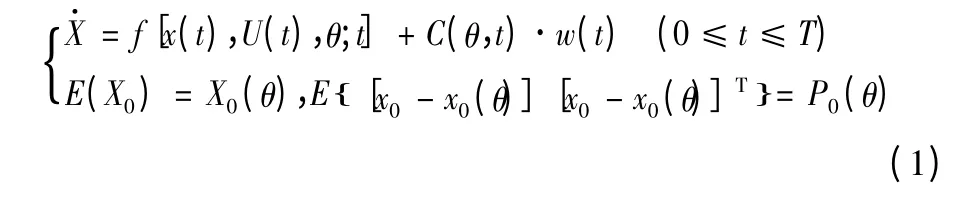
式(1)中，X(t)∈Rn×1，U(t)∈Rr×1，θ∈Rn×1是待估计参数矢量，C∈Rn×q是过程噪声分布矩阵，w(t)∈Rq×1是随机过程噪声矢量，均值为零的白噪声。

数理统计理论证明极大似然估计有如下重要性质:

描述观测矢量与状态矢量关系式的观测方程组取为离散形式:

本文采用j 表示新增的信息，v(tj)∈Ri×1是观侧噪声，是均值为零的高斯随机白噪声，且w(t)和v(tj)独立无关。

对于以上非线性动力学系统，新息v(j)及其方差B(j)是可以根据卡尔曼滤波给出;应用广义卡尔曼滤波。得状态预测方程组:

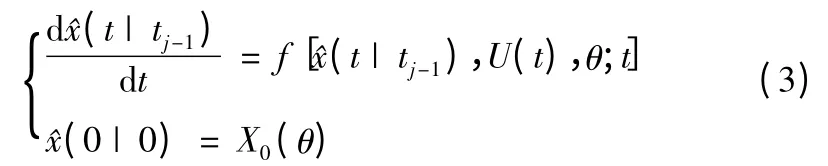
协方差预测方程组:

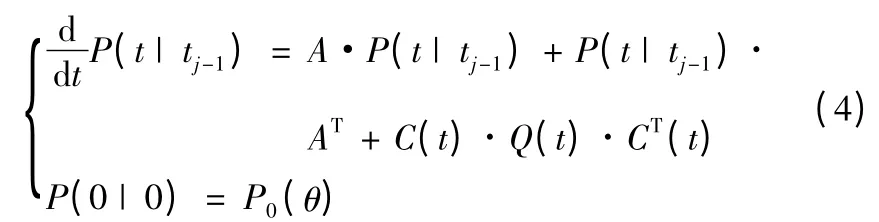
测矩阵和系统矩阵采用线化处理得到:

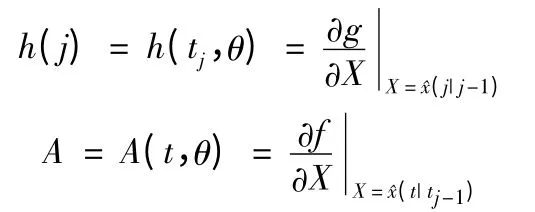
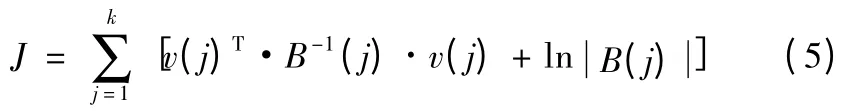
对于j=1 可以根据初始条件直接结合式(3)和式(4)求出预测值(t1|t0)=(1 |0)和预测协方差P(t1| t0)=P(1|0)(这里tj表示从连续方程得到的变量在当时取值，直接用j 表示离散值或固定值)，在下一步向j =2 递推过程中实际上在区间t∈［t2，t3］上求解，需要给出初值(1|1)和P(1|1)，需要求状态校正方程组:

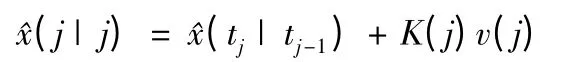
协方差方程组:

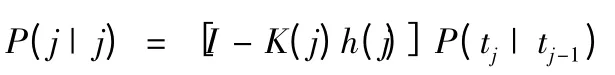
可以看出表达式非常复杂，无法直接给出式(3)的解析解，因此只能迭代求解。泛函极值的迭代求解法已有多种，如梯度法、共扼梯度法、最速下降法、麦夸特法、高斯法等等，实践证明牛顿一拉夫逊法对于动力学系统辨识是最有效的。

2 基于卡尔曼滤波最大似然参数估计算法步骤

极大似然参数辨识用于动力学系统的辨识的计算步骤如图1 所示。

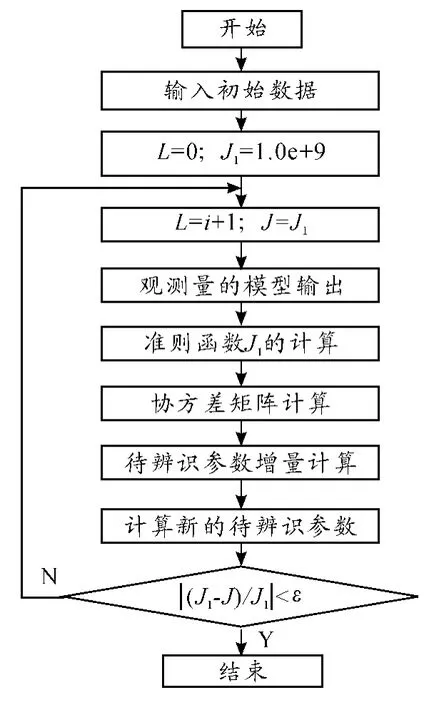
图1 卡尔曼滤波最大似然参数估计步骤

具体过程如下:

1)输入初始数据。参数的初估值θ0，状态初值X0:待估计参数θ 的上限和下限值;动力学系统试验的观测量和控制输入的实测值Zi，Ui(N 个实测数据点)。

3)准则函数J1的计算。利用模型输出Yi和实测数据Zi，求得J1。

4)协方差矩阵计算。利用模型输出Yi和实测数据Zi，求得。

5)待辨识参数增量Δθ 的计算。用中心差分法计算出灵敏度矩阵，利用Zi，Yi，求得Δθ。

6)计算新的θ。θi=θi-1+Δθi检验所得θi中是否有某个元素所给的上、下限。

图1 中状态初值X0可取为t0时刻的实测值，或取由实测值Z(t0)从观测方程算出的状态初值X0。参数初值θ0可取过去试验结果或理论计算结果，θ 上限和θ 下限按待辨识参数的物理意义结合实际情况给定。收敛指标ε 根据辨识精度要求事先给定，一般可取ε≤0.01。

这种改进主要表现在三个方面，即算法的优化、是否考虑过程噪声以及灵敏度的计算等。极大似然法具有集中处理数据的特点，即对一段时间历程上的数据集中分析，直接得到所需的气动参数，此方法也具有较高的精度，其估计具有一致性和无偏性。但是，它也有缺点，主要是计算所需时间较长，易于进行集中处理而不适合在线实时处理。

3 结果与分析

依据上述方法、步骤，通过基于卡尔曼滤波最大似然参数估计方法进行气动数据的辨识，辨识结果与真实固定翼风洞气动参数比较，结果如下:

图2 给出了气动系数Cx、Cy、Cz辨识曲线与参考曲线的比较。可见，通过基于卡尔曼滤波最大似然参数估计的气动参数辨识方法是有效的，辨识结果具有较高可信度，有利于气动参数辨识。

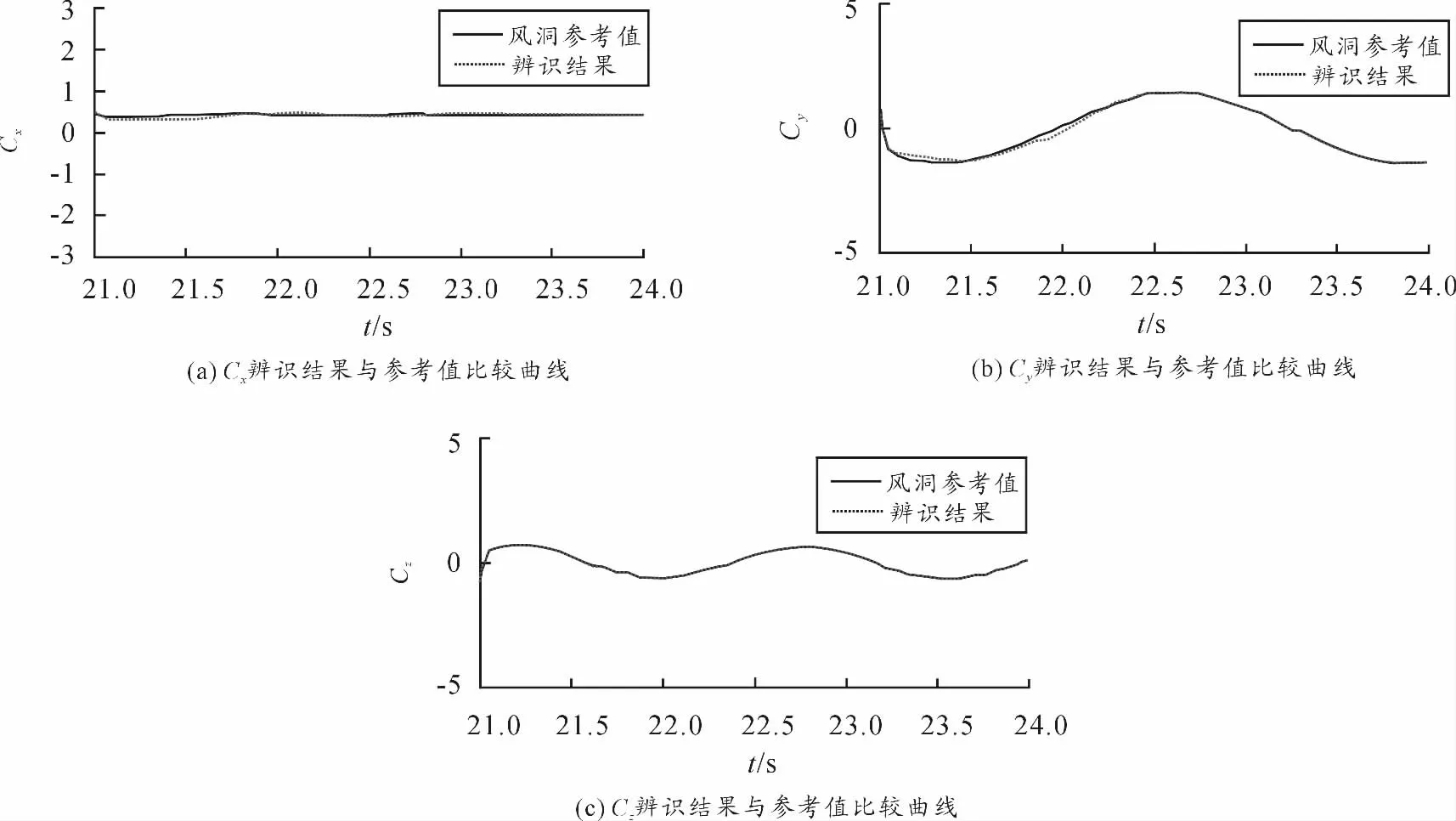
图2 Cx、Cy、Cz 辨识结果与参考值比较曲线

［1］彭晓刚.飞行器气动力系数小波网络建模研究［D］.哈尔滨:哈尔滨工业大学，2006.

［2］汪清，钱炜祺，何开锋.导弹气动参数辨识与优化输入设计［J］.宇航学报，2008，5（6）:12-16.

［3］邹新生，李春文.飞行器参数辨识的一种演化计算力法［J］.电光与控制，2006，13（2）:15-17.

［4］蔡金狮.动力学系统辨识与建模［M］.北京:国防工业出版社，1991.

［5］Dennis J，Robert F. Stengel. Identification of Aerodynamic Coefficients Using Computational Neural Networks［J］.AIAA Journal of Guidance Control and Dynamics.1993，16（6）:101-105.

［6］Hamel P G，Jategaonkar R V. Evolution of flight vehicle system identification［J］.Journal of Aircraft，1996，33（1）:9-28.

［7］WANG X P. Aerodynamic parameter flight vehicles based on adaptive genetic［J］. Journal of Astronautics，2003，12（3）:303-308.