EFP侵彻钢靶板过程的光滑粒子法数值模拟研究
2013-07-03苏文周
苏文周
(第二炮兵工程大学 士官学院,山东 青州 262500)
爆炸成形弹丸(explosively formed projectile,EFP)[1-2]作为反坦克装甲、打击舰艇的有效武器,在现在战争中发挥着重要的作用。EFP 主要是利用聚能原理,通过装药的爆轰作用,高温高压的爆轰产物作用于药罩,使药罩发生极大塑性变形而经过压垮、翻转形成一个较高质心速度和特定结构形状的弹丸,进而动能侵彻目标。目前国内外对于爆炸成形弹丸及其对靶板的侵彻破坏效应的研究主要是通过大量的实验来完成,其中由于药型罩的微小变化会引起EFP 性能的很大变化,靶板厚度的不同对破坏模式同样影响很大,因此这些均属于设计研究的关键。然而经过大量的实践证明,依靠射击试验来选取理想的结构方案是很不经济的,而且周期长。随着计算机及软件技术的发展,利用计算机来进行模拟和仿真逐步变为现实,同时该选取最优方案的方法既省时又经济。因此,对于该过程的数值模拟对于EFP 战斗部的研究与设计具有重要意义。
传统用于计算该过程的方法主要为有限差分法(FDM)、有限元法(FEM)或有限体积法(FVM)等基于网格的数值方法进行离散求解,计算中不可避免的出现网格的扭曲和缠绕(针对Lagrange 网格离散)或界面追踪复杂,精度较低(针对Euler 网格离散)的问题。光滑粒子流体动力学(smoothed particle hydrodynamics,简称SPH)方法作为一种无网格粒子方法,在对爆炸成形弹丸进行弹塑性流体动力学计算,对钢靶板进行大应变、高应变率的变形计算时可避免网格重分及算法耦合,因此非常适合此类问题的求解。最早应用SPH方法模拟爆炸的可追溯到Swegle 等[3],而Libersky[4-5]最先将SPH 方法应用于高速冲击领域,随后等Liu[6-7]应用SPH方法模拟了聚能装药的爆轰过程,Qiang[8]等运用Ott-Schnetter 提出的修正SPH 方法对聚能装药射流过程进行模拟,分析了不同的起爆方式对射流的影响。
本文在Qiang 等[9-10]提出的完全变光滑长度SPH 方法的基础上,与Ott-Schnetter[11]提出的修正SPH 方法结合处理爆炸和冲击过程中密度和光滑长度变化剧烈问题以及多介质界面问题,同时将含损伤的Johnson-Cook[12]本构模型引入到SPH 方法中处理钢靶板在高速冲击作用下的变形损伤问题,对聚能炸药爆炸挤压形成弹丸进而对钢结构靶板进行侵彻整个过程进行了数值模拟,并对侵彻过程中射流头部特定点处的速度变化过程进行了分析,同时为更充分的描述药型罩对于弹丸性能的影响以及钢结构靶板在高速弹丸冲击侵彻作用下的破坏损伤效应,对另外两种不同尺寸药型罩及不同尺寸的靶板进行了设计并进行了数值试验,结果表明SPH方法非常适合模拟诸如高速成型弹丸冲击钢靶板等涉及爆炸与冲击大变形多介质问题。
1 SPH 基本方程
SPH 基本方程通常由两个关键步骤完成构造,一是将场函数利用核函数近似方法进行积分表示,二是将将函数进行粒子近似。对于系统中物理量 f (r) 及其导数▽· f (r )的SPH 粒子离散形式:

式(1)、(2)中m,ρ,r 分别表示粒子的质量,密度和位置矢量,Wij=W( ri-rj, h )为核函数,h 为光滑长度,通常选用三次样条核函数[13]。
本文算例涉及爆炸与冲击、大变形大扭曲等密度和光滑长度变化剧烈问题,为更好地解决这些问题,本文采用完全变光滑长度SPH 方法[9],同时采用Ott-Schnetter[11]提出的修正SPH 方法解决药型罩和爆轰气体间密度梯度较大带来的间断面不稳定性问题,结合后的方程组如下

式(3)中Wij=W ( xi-xj,h),为核函数,它的选取直接影响计算的误差和稳定性,通常选用三次样条核函数;▽iWij表示核函数对i 粒子坐标的空间导数,vij=vi-vj;σ 为总应力张量,σαβ=-Pδαβ+ταβ;Πij为人工粘度;h 是插值核宽度的一种度量,称为光滑长度,表示W 不显著为零的取值范围,控制着SPH 粒子的影响域,通常设定,k=2 时W=0,在这里考虑光滑长度h 为空间和时间的函数,在连续方程中将其对时间求导,即

对于光滑长度变化率dhi/dt 与密度变化率dρi/dt 之间相互耦合而带来的难以显示求解的问题,本文采用参考文献[9]中的迭代的方法求解密度方程和光滑长度。
在计算的工程中,为避免拉伸不稳定的产生,本文采用Monaghan[14]和Gray[15]提出的人工应力方法解决该问题,它的思想即为避免两粒子过于靠近而在其中间施加一排斥力,方法是将在式(3)中动量方程施加下式

式(5)中,fij=W(rij)/W(Δp),Δp 为初始的粒子间距离,rij为粒子i 和j 的距离,n >0。SPH 计算时,通常比率h/Δp 是常数,W(Δp)即为常量。实际计算时,h 决定于密度的变化,由完全变光滑长度方程决定

Ri,Rj分别由相应散射方程求出。在本文算例中仅需要对静水压力进行修正便可满足要求,即当压力Pi<0 时

否则

同理可得Rj。通常,ε 取值为0.3。
2 炸药及药型罩材料模型
本文模拟中,炸药选用TNT,其爆轰速度由试验测得为6 930 m/s。对于波轰气体使用标准的JWL 状态方程来得到气体压力。

式(9)中ρ0为TNT 炸药的初始密度1 630 kg·m-3,v =ρ0/ρ为炸药初始密度和爆轰气体的比值,e 爆轰气体的比内能,A,B,R1,R2,w 为由试验拟合得到的系数,数值分别为A=371.2 GPa,B=3.231 GPa,R1=4.15,R2=0.95,w=0.3。
药型罩选用金属铜材料,状态方程选用Mie-Gruneisen 状态方程

其中
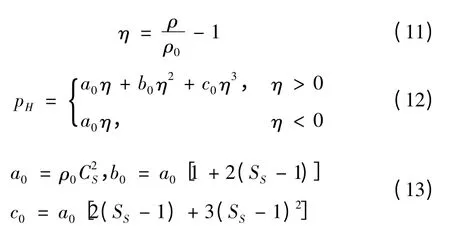
铜的密度为ρ0=8 530 kg/m3,式中各系数为Γ =1.99,CS=3 940,SS=1.489。
3 靶板本构模型及状态方程
3.1 屈服强度模型
钢结构靶板材料在高速弹丸冲击侵彻作用下,会达到材料的屈服极限而产生损伤,为更好地描述材料的屈服应力及损伤演化,本文引入Langseth M[12]等提出的改进Johnson-Cook 强度本构模型(图1),在该模型描述中将屈服强度表示为等效应变、等效应变率、损伤变量及材料温度的函数

式(14)中A,B,C,n,m 为材料常数,无量纲温度T*=(T-T0)/(Tm-T0),T0为室温,Tm为材料熔点。r 为累积损伤塑性应变,r=(1-D)p=(1-D=/,p 为累积塑性应变为用户自定义的参考应变率。D 为损伤变量值,当D=0 表示材料未发生损伤,D=1 表示材料完全失效。而实际当材料出现裂纹时,损伤变量临界值一般小于1,失效准则为D=DC≤1,DC为损伤变量临界值。
3.2 累计损伤模型
文献[12]将损伤变量D 描述为累积塑性应变p 的函数,即

其中,pf为材料断裂塑性应变,与材料的应力三轴度、应变率及温度相关,pd为材料的损伤阈值。pf采用由Johnson 和Cook[16]提出的剪切损伤演化模型描述

σ*=σm/σeq为材料的应力三轴度,σm=(σx+σy+σz)/3 为材料的平均正应力,D1~D5为材料的常数。靶板压强采用式(10)Gruneisen 状态方程计算。
4 爆炸成形弹丸侵彻钢靶板的计算
在算例计算中,采用的靶板材料参数见表1。爆炸成形弹丸侵彻钢结构靶板的过程包括炸药的爆轰、药罩的挤压、弹丸的形成及发展、弹丸高速冲击靶板、靶板损伤破坏等过程。计算采用的装药模型及靶板模型如图2(a)所示,药柱宽度40.00 mm,装药头长11.45 mm,药孔长度32.875 mm,药罩外部圆弧半径为27 mm,内部圆弧半径为23 mm,药型罩厚度4.00 mm,炸高为40 mm,靶板尺寸分100 mm ×10 mm。炸药采用点起爆的方式,起爆点为(0,0.05),具体粒子配置如图2(b),粒子间距均为0.5 mm,其中TNT 炸药为23 806 个粒子,药型罩为2 958 个粒子,靶板为16 000 个粒子。光滑长度取1.5 倍粒子间距,时间积分采用蛙跳格式,时间步长为0.01 μs。

表1 钢结构靶板材料参数
图2 给出了炸药爆轰药罩被挤压(a),弹丸形成(b),弹丸冲击侵彻靶板形成开孔(c)及靶板完全破坏(d)的过程。可以看出药型罩在炸药爆轰波压力作用下,药型罩中心首先开始加速,罩的边缘随后开始加速,除中心外的药罩不仅产生轴向拉伸变形,同时被驱动向对称轴运动,药型罩随后发生翻转,从而形成头部对称,尾部成喇叭型且中空的弹丸,所形成的弹丸重心集中在前段,所以其飞行稳定性较好,且径向压合作用不明显,因此很容易形成有利于穿透装甲目标的侵彻体。由图2(c)(d)可以看出,弹丸在垂直侵彻初期,弹丸变形较小,随着弹丸继续向前侵彻,靶板在压力的作用下向最小抗力方向产生塑性流动,靶板材料向周边产生金属堆积,形成翻起的花瓣形变形。弹丸继续向下侵彻,靶板中部的金属被弹丸挤压而产生横向位移,而靶板同时产生塑性变形。随着弹丸的继续侵入,靶板表面侵彻周边的凸起越来越大,靶后背面形成鼓包,同时靶体由于拉伸塑性变形的作用产生裂纹,直至彻底失效。
通过观察得到,该侵彻主要以前端弹丸为主,因此选取了弹丸中心头部粒子进行分析,图3 为该点的速度随时间变化曲线,可以看出,药型罩在0.005 ms 时受到炸药的挤压开始加速,在0.02 ms 左右时达到速度最大值1 440.976 m/s,射流头部在0.043 ms 后开始与靶板接触,速度降低幅度较大,动能转化为内能,造成靶板的破坏,随着侵彻的深入,动能逐渐减小,直到靶板彻底损伤破坏,速度基本保持不变,约为660 m/s。
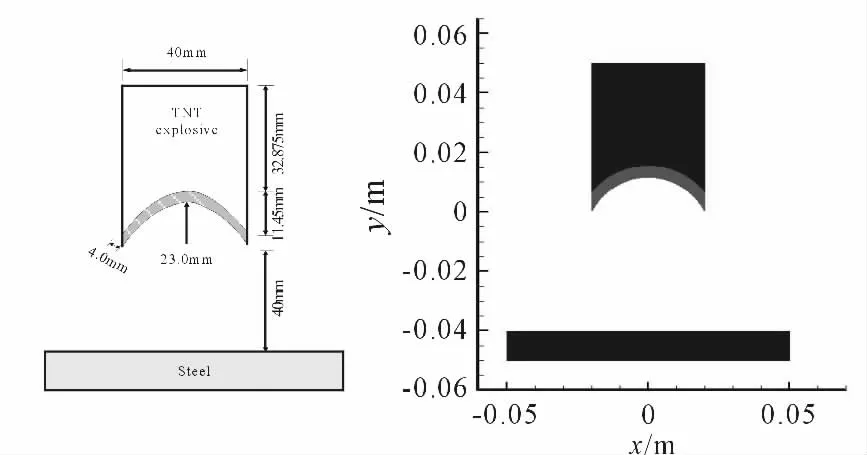
图1 算例模型结构
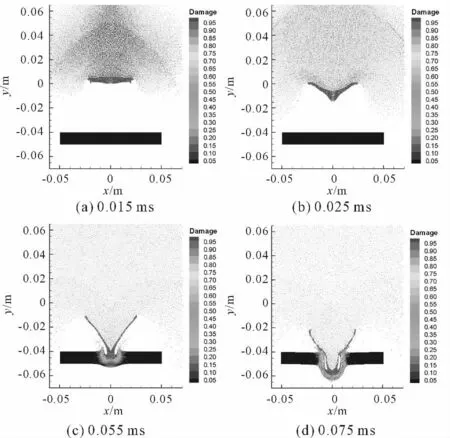
图2 爆炸成形弹丸侵彻钢结构靶板的过程

图3 射流头部特定点处速度时间曲线
文献研究表明[17-18]影响弹丸速度的因素有装药长径比、药型罩壁厚、壳体厚度、药型罩曲率半径、药型罩材料、起爆点位置等等。本文为验证算法的正确性,同时检验药型罩厚度对靶板侵彻的影响,选取另外两种不同厚度药型罩的弹丸侵彻靶板进行了数值试验。药型罩厚度分别为2.16 mm,5.86 mm,粒子数分别为1 562 个和4 234 个。计算结果分别如图4、图5。图6 为选取的弹丸头部特定点进行追踪得到的速度时间曲线,从图6 中可以看出,当药型罩壁厚减小时,形成EFP 的速度将逐渐增加,2.16 mm 厚度药型罩形成的弹丸头部最大速度将达到2 191.46 m/s,因为药型罩壁厚减小将减小推动药型罩做功的炸药的能量,而相同炸药量的情况下使单位质量的药型罩获得的能量增加。而5.86 mm 厚度药型罩形成的弹丸头部速度不但较小,而且在形成弹丸的过程中由于药罩较厚,药罩头部在被挤压的过程中受塑性流动的影响,速度在增加时会出现一个反弹,持续0.01 ms 左右,而后重新回到最大速度点,如图7(b)。同时通过靶板的损伤情形可以看出,随着药型罩厚度的增加,靶板损伤后形成的单碎片的体积更大,弹丸的变形程度较小,而对孔径大小的影响不明显。

图4 2.16 mm 厚度药型罩成形弹丸对靶板侵彻过程
为进一步研究不同尺寸的靶板在高速弹丸的冲击作用下的破坏形式,本文选取了较上文算例更厚的靶板进行数值试验,靶板厚度为20 mm,SPH 粒子离散数目为22 000 个,靶板损伤变形过程如图7,由图可以看出,与前面薄形靶板变形不同的是,靶板在较大的冲击力的作用下,随着弹丸侵彻深度的增加,靶板塑性变形的增大,受压区域的金属材料相对于其余部分运动,在压缩范围的边缘产生强烈的剪切变形,形成剪切带,剪切变形产生的热无法及时向外传播,仅限于该狭窄的区域,该区域的材料强度下降而失稳。此时弹丸前方靶板材料的运动速度与弹丸速度基本相同,产生剪切型充塞破坏,如图7(d)。同时在开孔上部,可以看出明显的被撕裂部位边缘有明显的翻卷,而冲击波到达底部边缘后会发生波的发射,对钢板产生一定的损伤,研究表明冲击波是使钢板变形最终呈倒锥形的原因。因为冲击波到边缘反射后,将保护钢板将正向压力波向上推开,在塞状体中心破坏性较小。

图5 5.86 mm 厚度药型罩成形弹丸对靶板侵彻过程

图6 另外两种不同尺寸的靶板特定节点速度时间曲线
图8 为选取的弹丸头部特定点进行追踪得到的速度时间曲线,点A 为弹丸头部内节点(与炸药粒子直接接触),点B 为弹丸头部外节点(与钢靶板直接接触)。从图可以看出,内节点速度一般低于外节点速度,在冲击侵彻过程中,弹丸外部首先变形速度降低,形成金属堆积,而后弹丸内部开始速度降低,直至内外节点速度相同,靶板形成充塞破坏。

图7 较厚靶板在高速弹丸侵彻下的损伤变形过程

图8 弹丸头部特定节点速度时间曲线
5 结论
本文运用无网格SPH 方法计算得到了爆炸成形弹丸形成、发展、高速冲击钢结构靶板及靶板变形损伤整个过程,由模拟分析可知:
1)SPH 作为一种无网格Lagrangian 粒子法,能有效解决传统网格法在计算爆炸成形弹丸侵彻钢结构靶板时遇到的Euler 网格界面追踪复杂或Lagrange 网格扭曲和缠绕的问题。本文基于完全变光滑长度SPH 方法与Ott-Schnetter 提出的修正SPH 方法相结合的方法,模拟了爆炸成形弹丸侵彻钢靶板的整个过程,结果表明这一处理方法有效解决了爆炸与冲击中光滑长度变化剧烈的问题以及多介质界面上大密度间断带来的计算不稳定问题。
2)本文运用含损伤的JC 本构模型来描述钢结构在高速冲击下的变形损伤特性,从模拟结果来看,不仅得到了破孔的形状,而且对靶板在高速侵彻作用下形成的损伤裂纹、充塞破坏等变形损伤细节描述精确,与实际物理现象符合。
3)通过对三种不同厚度药型罩及不同厚度靶板的冲击破坏试验分析可得:随着药型罩厚度的增大,形成的弹丸前端速度逐渐减小,靶板受侵彻形成的碎片体积更大。随着靶板厚度的增加,靶板破坏的形式将逐渐发生改变,更加倾向于形成大块碎片,甚至产生充塞破坏。
[1]宁俊生.成形装药和爆炸成形弹丸的研究进展[J].兵器材料科学与工程,2004,27(6):65-72.
[2]梁争峰,胡焕性.爆炸成形弹丸技术现状与发展[J].火炸药学报,2004,27(4):21-25.
[3]Swegle J W,Attaway S W. On the feasibility of using smoothed particle hydrodynamics for underwater explosion calculations[J]. Computational Mechanics,1995(17):151-168.
[4]Libersky L D,Petscheck A G.Smoothed particle hydrodynamics with strength of materials,in H.Trease,J.Fritts and W.Crowley(ed.):Proceedings of The Next Free Lagrange Conference[C]//SpringerVerlag,NY,1991,395: 248-257.
[5]Libersky L D,Petscheck A G,Carney T C,Hipp J R,Allahdadi F A.High strain Lagrangian hydrodynamicsa three-dimensional SPH cde for dynamic material response[J].Journal of Computational Physics,1993,109:67-75.
[6]Liu M B,Liu G R,Zong Z,et al. Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology[J].Computers & Fluids,2003,32:305-322.
[7]Liu M B,Liu G R,Lam K Y,et al.Meshfree particle simulation of the detonation process for high explosives in shaped charge unlined cavity configurations[J]. Shock Waves,2003(12):509-520.
[8]Qiang H F,Wang K P,Gao W R.Numerical Simulation of Shaped Charge Jet Using Multi-Phase SPH Method[J].Transactions of Tianjin University,2008(14):495-499.
[9]强洪夫,高巍然.完全变光滑长度SPH 法及其实现[J].计算物理,2008,25:569-575.
[10]强洪夫,王坤鹏,高巍然.基于完全变光滑长度SPH 方法的HE 爆轰过程的数值试验[J].含能材料,2009(17):27-31.
[11]Frank Ott,Erik Schnetter.A modified SPH approach for fluids with large density differences[J].physics/0303112.
[12]Langseth M,Hopperstad O S,et al.Ballistic penetration of steel plates[J]. International Journal of Impact Engineering,1999(22):855-886.
[13]Monaghan J J. Smoothed particle hydrodynamics[J]. Reports on Progress in Physics,2005,68:1703-1759.
[14]Monaghan J J.SPH without a tensile instability[J].Comput Phys,2000,159:290-311.
[15]Gray J P. Monaghan J J,Swift R P. SPH elastic dynamics[J]. Comput Methods Appl Mech Eng,2001,190: 6641-6662.
[16]Johnson G R,Cook W H. Fracture characteristics of three metals subjected to various strains,strain rates,temperatures,and pressures[J]. Engineering Fracture Mechanics,1985,21(1):31-48.
[17]谢文,龙源,岳小兵,等.钢模拟爆炸成形弹丸(EFP) 飞行特性及对大问隔靶的侵彻实验[J].解放军理工大学学报:自然科学版,2002,3(1):66-70.
[18]周翔,龙源,岳小兵.76mm 口径EFP 成形过程数值模拟及影响因素研究[J].弹道学报,2003,15(2):59-63.
[19]陈雪礼,王克印,苌军红,等.某型弹丸侵彻深度的影响因素[J].兵工自动化,2011(3):6-7.
[20]朱峰,朱卫华,颜君来,等.锥头弹弹尖角度对侵彻效果影响问题的数值分析[J].四川兵工学报,2011(3):139-141.
