变桨距系统多变量协调控制策略研究

张宏立，田勇

（新疆大学 电气工程学院，新疆 乌鲁木齐830047）

1 引言

风力发电是在现阶段的新能源开发过程中最具开发前景的技术之一，在世界各国的共同努力下，风力发电机组控制技术也日趋成熟和完善。 为了进一步提高对风能的利用效率，风力发电机控制技术已朝着大型化变桨型方向发展，兆瓦级变桨距风力机已成为国内外风电市场上的主流机型[1]。 相对于传统的中小型风力机，现代大型变桨距风力机的叶片尺寸较大，其叶片长度可达上百米，如何在高风速下对风机叶片实现精确变桨是风力发电机控制技术中的一个关键问题。

近年来，在统一变桨距控制技术的基础上衍生出了独立变桨距控制技术，该技术降低了塔影效应和风切效应对风力机叶片和风力机塔架内部的各种部件产生的疲劳载荷等问题，同时在高风速下还能够保证风力发电机的额定功率输出。

目前国内外的独立变桨距控制技术大多采用与各个叶片配套的独立回路控制系统，通过变桨系统根据实际风速情况来发出变桨指令，由各个独立回路控制系统对叶片桨距角变化进行控制[2]。 由于整个风力机变桨系统为一个多变量的控制系统，这种独立回路控制技术忽略了变桨系统内部各个变量之间的耦合性。 在风力机的运行过程中，作用在风力机各个叶片上的气流大小、 惯性力等载荷均有所不同，独立回路控制技术无法获取除自身以外的桨叶空间位置、 桨叶受力情况等信息，不能实现系统精确变桨，在这种情况下容易造成叶片弹性力不均引起的塔架振动和叶片疲劳载荷的增加。 基于此，本文针对变桨系统中的特点，提出了一种同步协调控制策略致力于对变桨系统的多变量控制技术进行研究。

2 变速变桨距风力机的控制策略

图1中风力机的转矩—速度特性曲线描述了变速变桨距风力发电机的基本控制策略，从图1中可以看出由风力机的输出转矩、 转速以及输出功率的特性曲线所形成的区域为风力发电机的稳定运行区间，即图1中的oABC 所构成的区间范围。 在这个稳定的运行区域内可以采用多种控制方式对风力机进行控制。 对于传统的恒速运行的风力发电机，其工作区间处于图1中的XY 这条直线上，根据恒速运行风力机的运行特性曲线可以看到，它仅有一个工作点运行在最佳风能利用系数曲线Cpmax上。

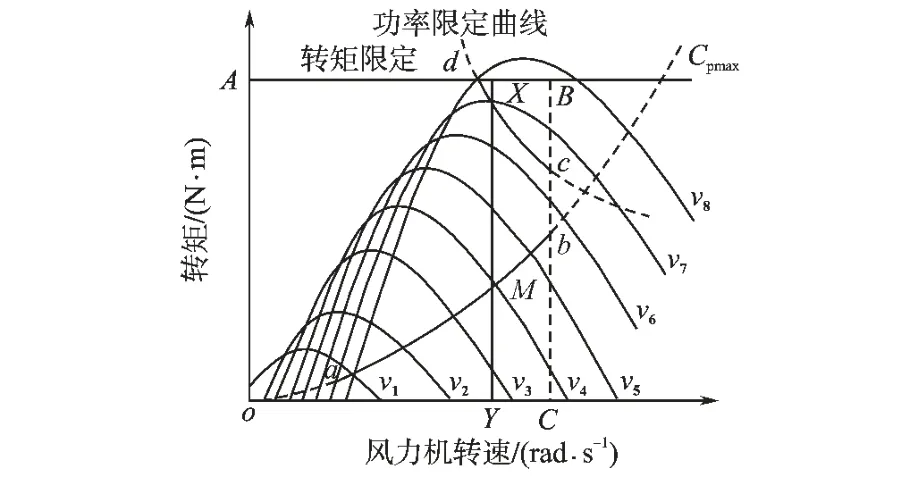
图1 不同风况下的风力机转矩—速度特性曲线Fig.1 Torque-speed characteristic curves of wind turbine under different wind conditions

变桨距风力机的运行方式与恒速运行的风力机不同，变速变桨距风力机的工作区间是由多条曲线组合而成，当风力机在其额定风速以下运行时，变桨系统会调整叶片桨距角使其能够获得最大转矩，此时风力机运行在图1中的最佳风能利用系数曲线的ab 段上，其中a 点和b 点的转速为风力机的变速运行范围。 由于b点的转速已达风力机的极限，从此时到风力机的最大输出功率点的范围内风机转速将维持恒定不变。 当风力机的输出功率到达其极限输出c 点后，若此时风速继续增大，则需进一步调节叶片的桨距角来降低风力机对外界风功率的吸收，保持风力发电机的额定功率输出。

3 变桨距系统与数学模型

3.1 独立电动变桨系统

根据控制方式可将变桨系统分为统一变桨和独立变桨，统一变桨是指系统发出变桨指令并通过唯一的变桨执行机构来调节3 个叶片的桨距角[3]。 独立变桨系统则是通过3 套不同的变桨执行机构来调节叶片的桨距角，通常情况下采用变桨电机作为变桨执行机构的驱动装置。 独立变桨距系统包括连接器、滑环、限位开关、旋转编码器以及变桨电机等装置[4－5]。

图2为变桨系统的内部结构分布，在图2中为其中一个桨叶的电动变桨系统。

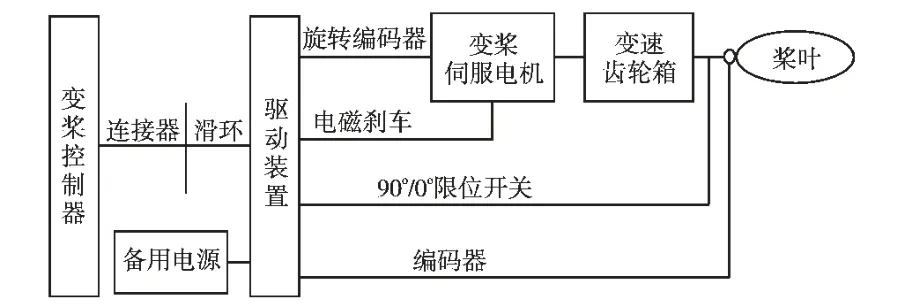
图2 独立电动变桨系统结构Fig.2 Individual electric pitch system structure

3.2 独立电动变桨系统数学模型

在风力发电过程中，力矩的传递主要通过风轮主轴与齿轮箱的配合来实现，整个齿轮箱变速系统即为风机的传动系统[6]。 其主要作用在于将风轮主轴上的角速度ωT通过变速箱的作用使其转换为发电机转子轴的速度ωmec，其表达式可用下式表示：

式（1）反应了风轮主轴与发电机之间的角速度关系，其中KT为齿轮箱的增速比。 在齿轮箱的作用下，使得风轮主轴的转矩TT与风力发电机转子侧的输入转矩Tmec也存在着如下关系：

风轮主轴转动惯量与发电机转子侧转动惯量之间的关系为

式中：Jt为风力发电机转子转动惯量，kg·m2；JT为风力发电机风轮主轴转动惯量，kg·m2。

根据以上推导过程，可以得到风力发电机变桨系统传动系统的数学模型如下：

4 风力机多桨耦合协调控制系统

4.1 变桨系统耦合协调控制策略

桨叶的同步性能主要通过同步误差来反映，通过分析，我们认为同步误差应该有2 种：一种是跟踪误差，即单个桨距调节过程中与期望值的偏差； 另一种是同步动态误差，即桨距调节过程中桨叶间的误差。 为了防止变桨过程不同步引起的风机叶片弹性力不均进而使得塔架振动和叶片疲劳载荷的增加对风机造成的影响，本文采用了交叉耦合协调控制技术来进一步提高风力发电机运行过程中的变桨精度，控制方案如图3所示。

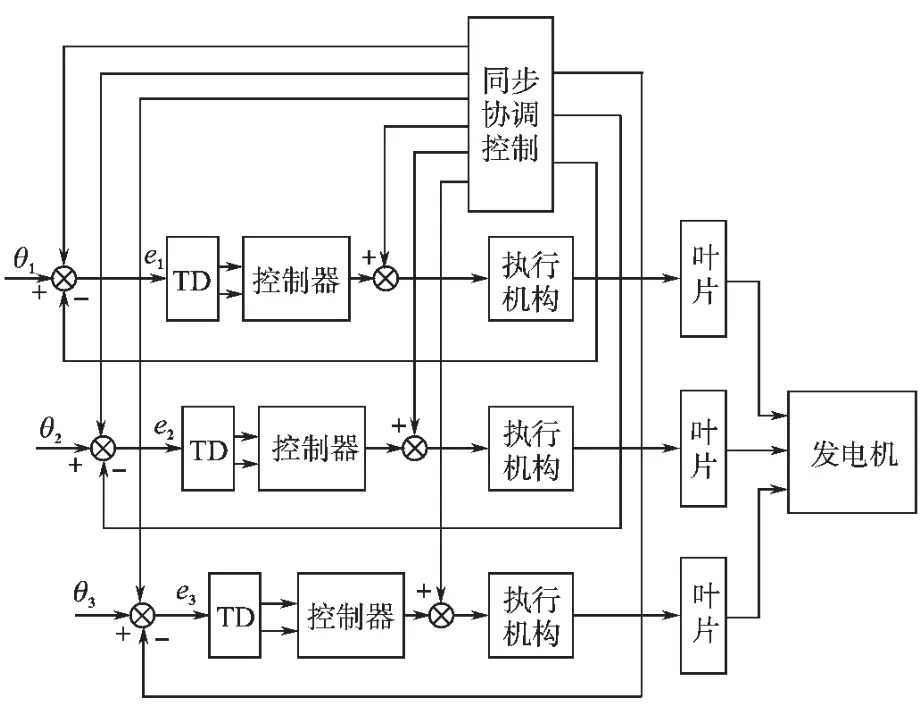
图3 变桨系统交叉耦合协调控制系统Fig.3 Pitch control system of coordination and cross-coupled

在图3所示的控制系统中将从2 方面来提高变桨系统的同步性：一是采用先进的控制策略及补偿技术，提高各桨距系统的控制特性的一致性或增益参数匹配能力，减小各桨叶的跟踪误差，从而间接减小桨叶间的同步动态误差。 在单桨控制方面采用滑模变结构控制（sliding mode control）策略，该策略在非线性控制系统中具有较好的鲁棒性，滑模变结构控制方法的主要思想在于利用高速的开关控制律，驱动非线性系统的状态轨迹渐近地到达一个预先设计的状态空间曲面上，使系统处于滑动模状态； 二是采用交叉耦合的误差补偿办法，在不改变各单桨控制策略的情况下，通过向各桨提供附加补偿来主动抑制系统的同步误差。

为了使3 个桨叶之间的动态特性相匹配，引入了交叉耦合补偿控制策略，该控制策略是一种基于时间的动态控制方法，其主要控制思想是通过获取的各个桨叶的跟踪误差信息来实时估算桨距角误差，根据设计的控制律对桨距角误差进行反馈性补偿，并将补偿分量分解到变桨距系统的各个执行机构中。 在交叉耦合控制策略中，通过一种基于Lyapunov 函数的交叉耦合控制规律来实现变桨过程中的多桨叶协调控制，并设计一个包含跟踪误差的Lyapunov 函数，可以通过调整变桨系统桨叶误差权值的配置，采用积分backstepping 技术设计风力发电机变桨距系统的控制规律，该控制规律包含了桨叶的空间位置信息、 桨叶角度偏差信息以及桨叶角度偏差导数等信息，通过时变PID 控制，可以实现系统的局部稳定性，再通过调节风机桨叶的跟踪误差的权数来提高整个变桨系统的同步协调性能。

4.2 多桨耦合协调控制器设计

交叉耦合协调控制是一个多变量、 非线性以及带有时变性的控制系统，对于这种复杂的控制系统的稳定性分析和参数优化具有较大的困难。 从图3中可以看到，由于本文所设计的交叉耦合协调控制器的输出附加在各个桨叶的空间位置控制器的输出上，一次交叉耦合协调控制器的输出必须要与风力机各个桨叶的空间位置控制器的输出一致，即在增益系数上要与之相对应，从而保证变桨系统的精确输出。

本文中的单桨控制器采用常规的PID 控制器，在交叉耦合协调控制器的作用下，系统的控制目标有2 个：一是最大限度地保持各个桨叶空间位置的输出精度； 二是尽可能地保持变桨过程中的同步性。

根据以上协调控制方案，在风力发电机变桨控制系统中，定义第i 个桨叶(i=1,2,3)的动力学方程为

式中：xi为变桨系统中第i 个桨叶的空间位置；Hi(xi)和Ci(xi,)分别为惯量和非线性的影响；Fi(xi,)为系统摩擦力和其他扰动的影响；τi为输入力矩。

在系统中，定义第i 个桨叶的位置误差为

式中：xdi(t)为系统给定的桨距角信号。

在同步控制中，还需同时考虑两桨之间的同步误差，将2 个桨叶间的同步误差定义为

在风力发电机的变桨控制过程中，除了包含单桨误差ei(t)和同步误差ε(t)，此处引入一个耦合误差e*i(t)为

在耦合误差定义式中，β 为一个正耦合系数，在以上式子中，同步误差分别从2 个相反的方向作用于耦合误差e*1(t)和e*2(t)，这能够大大降低系统的同步误差，同时在此也命令矢量ui(t)为

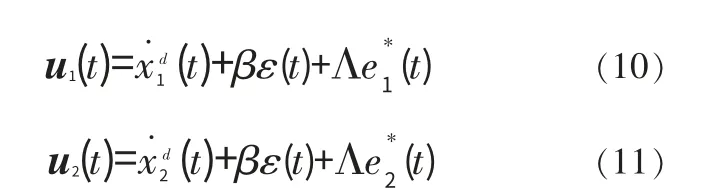
通过式（10）、式（11）可以得到调节耦合位置误差和速度误差的矢量为

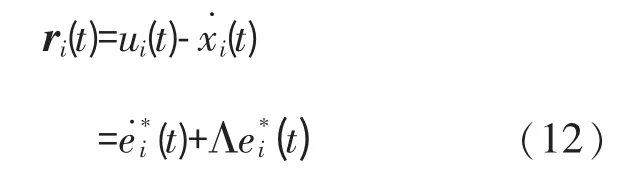
对于系统的控制器，其主要控制目标为设计输入力矩τi来限制耦合位置误差和速度误差的矢量ri(t)，从而能够使得耦合误差e*1(t)和趋于零。 则控制器为

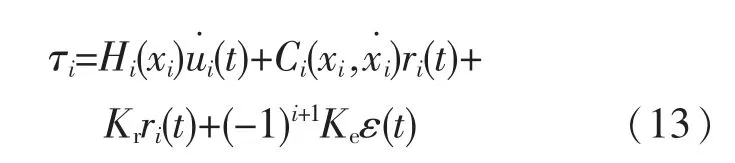
在式（13）中，Kr和Ke为正数的增益常量。将式 （13）代入风力机动力学数学模型式（5）中，得到系统的闭环动力学方程为

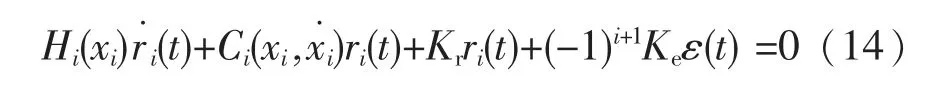
为了验证同步控制算法对系统误差的影响，现对算法的桨距角位置跟踪误差和桨叶空间位置的同步误差的收敛性进行证明，现设t→∞时，ei(t) →0 和ε(t) →0。

对风力机变桨速率v(t)时间的导数为

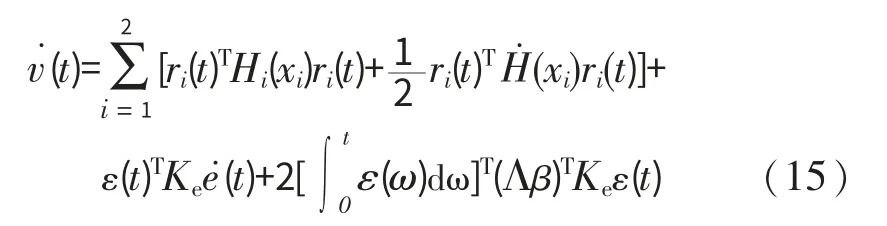
在闭环方程式（14）的两边同时左乘ri(t)T，再减去v（t）对时间的导数得到：

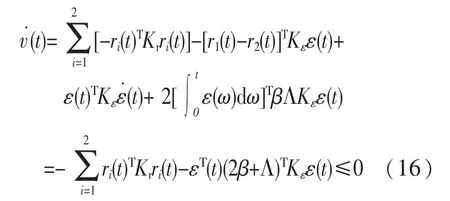
根据式（16）可得到ri(t)和ε(t)的L2范数是有界的。根据式（12）中也可得到(t)和(t)是有界的，对式（8）和式（9）求导可推得(t)有界。 如果t→∞时，则ri(t) →0 和ε(t) →0。由此可以根据式（12）中的ri(t)的定义推得当t→∞时，→0且(t) →0。 根据式（7）可得：

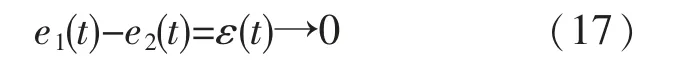
将式（8）和式（9）相加得到：

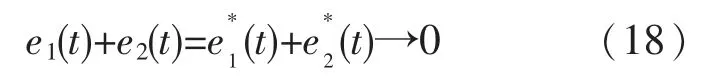
通过联立式（17）和式（18）可得到当t→∞时，e1(t)→0 的同时e2(t)→0，由此可以看出同步控制算法能够保证变桨系统的跟踪误差和同步误差渐进误差收敛到零。 在传统的解耦控制过程中，更多的是在考虑单桨误差ei(t)的收敛，通过对系统单桨误差的控制来提高变桨系统的控制精度。 但在对系统进行协调控制时，不但需要考虑单桨误差的影响，同时还应考虑单桨与其他桨叶的同步误差给系统带来的影响，从而提高风力发电机变桨距系统的变桨精度。

5 系统仿真与分析

本文选取额定功率为1.5 MW 的风力机变桨系统为研究对象，变桨系统中的桨叶伺服执行电机采用三相交流异步电动机，其额定功率为4.5 kW，最大转矩为75 N·m，制动转矩为100 N·m，转速为1 500 r/min。在湍流风速下模拟变桨系统的变桨信号给定, 图4中的虚线为系统模拟的桨距角给定信号。

图4 非协调状态下的桨距角输出Fig.4 Pitch angle output of non-coordination mode

图4中为风力机变桨系统在非协调控制状态下的桨距角输出，图4中用各种线性描述了3 个桨叶的实时变桨输出角度，从图4中可以看出各桨叶在变桨过程中对原始给定信号的跟踪性较差，且各个桨叶在变桨过程中未能到达变桨实时同步状态，在这种非精确变桨的情况下容易造成风力机叶片弹性力不均，进一步引起风机塔架振动和叶片疲劳载荷的增加，对风力机的运行安全和使用寿命造成一定的影响。

图5为风力机在非协调控制状态下各个桨叶相对于原始给定信号的跟踪误差，从图5中可以明显的看到各个桨叶的实时角度输出误差情况，在非协调控制状态下，起始时的最大误差可达12°，且在系统稳定运行阶段，其误差也在0°至3°间波动，误差限高达20%。

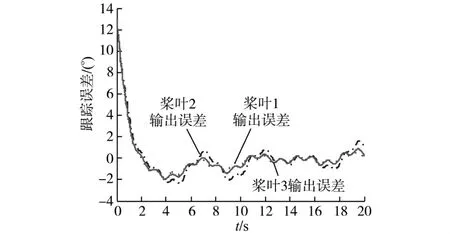
图5 非协调状态下各桨的跟踪误差Fig.5 Pitch tracking error of non-coordination mode

图6为风力机在协调控制器的作用下各个桨叶的桨距角输出，从图6中可以看到各桨对原始给定信号有很好的跟踪性。 在协调控制器的作用下，与图4中的桨距角输出相比，变桨系统的跟踪性能得到了较大的提高。

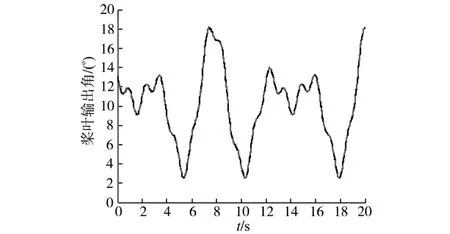
图6 协调状态下的桨距角输出Fig.6 Pitch angle output of coordination mode

图7为风力机在协调控制策略的作用下各个桨叶相对于原始给定信号的跟踪误差，从图7中可以看到在协调控制器的作用下，变桨系统的跟踪误差与非协调状态下的跟踪误差相比大大降低，最大跟踪误差仅为0.2°，通过协调控制器的调节，稳定运行状态时的跟踪误差保持在0.02°附近，这不但提高了变桨系统的跟踪性，同时也提高了各桨叶的变桨同步性。

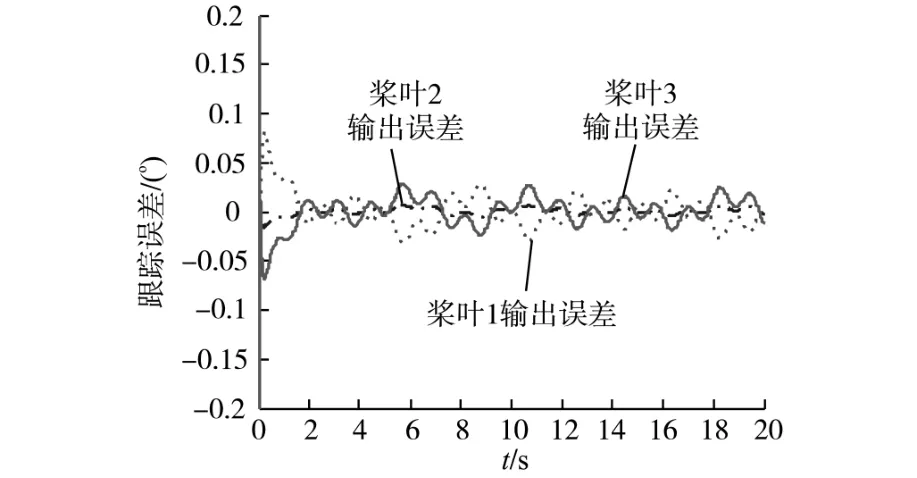
图7 协调状态下各桨的跟踪误差Fig.7 Pitch tracking error of coordination mode

6 结论

本文以风力机传统变桨控制策略为基础，并结合了独立电动变桨系统的多变量以及变量耦合性等特点，提出了多变量交叉耦合性协调控制策略。 并对两种策略在湍流风速下的仿真输出结果进行了比较分析。 其结果表明，风力机变桨系统在交叉耦合协调控制器的作用下，系统的变桨精度和桨叶的实时变桨同步性能得到了大幅度的提高，一方面能够使得风力机在高风速下保持对风能的最大利用效率，另一方面降低了叶片弹性力不均引起的塔架振动和叶片疲劳载荷，提高了风机运行的稳定性。

[1] Nagai M B，Ameku Kazumasa，Roy N J． Performance of a 3 kW Wind Turbine Generator with Variable Pitch Control System[J]．Applied Energy，2009，86（9）：1712－1722．

[2] 张雷，李海东，李建林，等．基于LQR 方法的风电机组变桨距控制的动态建模与仿真分析[J]．太阳能学报，2008，29（7）：781－785．

[3] 王斌，吴焱，丁宏，等．变速变桨距风电机组的高风速变桨距控制[J]．电力自动化设备，2010，30（8）：81－83．

[4] XIA Chang-liang．Integral Variable Structure Current Control of DFIG- based Wind Turbines Near Cut- in Speed [J]．International Journal of Modeling，2009，7（4）：338－345．

[5] Rothenhofer G，Slocum A．Technical Note：Reducing Pitch Error of a Linear Motion System Actuated by a Permanent Magnet Open Face Linear Motor[J]．Precision Engineering，2009，33（3）：305－309．

[6] 王亚飞，赵斌，许洪华．风电机组电动变桨距伺服系统的研究[J]．可再生能源，2011，29（4）：28－31．