同步发电机模型在MMC并网控制中的应用
2013-07-02刘喜梅
刘喜梅,陈 朋,张 群,赵 倩
(青岛科技大学自动化与电子工程学院,青岛 266042)
随着能源和环境问题的加剧,风能和太阳能等可再生能源[1]在一次能源中所占比例越来越大,但其分散、远离主网的特点却制约着这些新能源的进一步发展。当前,如何将这些新能源产生的电能既快速又经济的传输、并网已成为研究热点,而柔性直流输电技术凭借其经济、灵活、高质量、高可控性、能够将分散系统方便的连接在一起等优点[2],成为解决上述问题的最佳选择。模块化多电平换流器 MMC(modular multilevel converter)作为柔性直流输电的主要设备,能够有效地改善输出波形,降低开关及系统总损耗,提高换流系统的效率、可靠性及经济性[3]。因此,研究如何实现MMC并网具有较高的实用性。
本文应用同步发电机模型实现对MMC并网控制。在MATLAB/Simulink中搭建MMC模型,对该控制策略进行仿真研究,同时也对PI控制并网电流跟踪电网电压相位在MMC并网中的应用进行了仿真,并将两者的仿真结果进行了比较。比较结果表明,在基于同步发电机模型的MMC并网控制策略控制下,MMC并网冲击小,能够快速达到额定输出,实现友好并网。
1 模块化多电平换流器
模块化多电平换流器MMC,是一种新型模块化电压源型换流器[4],其拓扑结构[5~7]如图1所示。
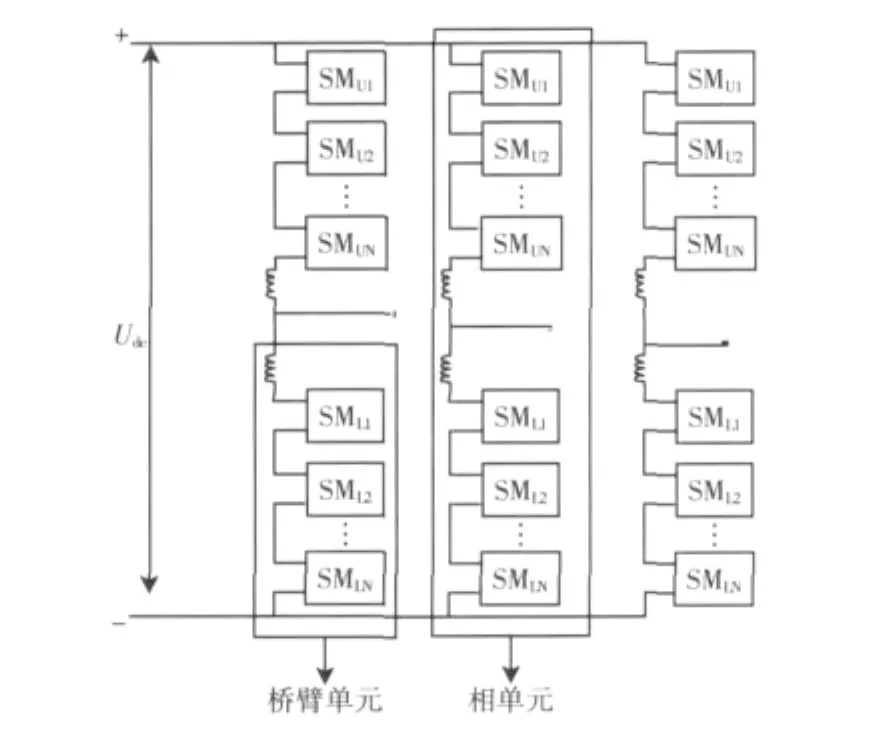
图1 三相MMC拓扑结构Fig.1 Topological structure of three-phase MMC
其中SM(sub-module)是子模块,其结构如图2所示。
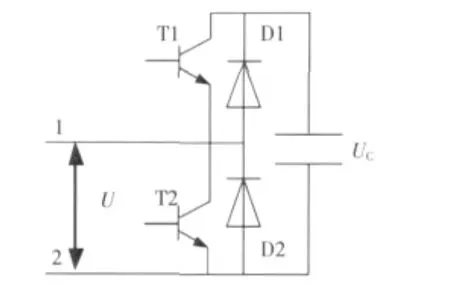
图2 MMC子模块结构Fig.2 Structure of MMC sub-module
由图1可知,MMC每相由上下两个桥臂构成,每个桥臂由N个子模块和一个电抗器串联而成。每个子模块由两个IGBT、两个反向二极管和一个电容构成,如图2所示。MMC在初始启动状态,每个子模块通过反向二极管D1同时给电容充电,使每个子模块上的电容电压都达到Udc/2N。当MMC正常工作后,必须保证上下桥臂共有N个子模块投入,即Nu+N1=N,其中Nu为上桥臂投入子模块数,N1为下桥臂投入子模块数。MMC通过触发各相桥臂中相应子模块上的开关器件、调节桥臂电压间的比率并串联叠加各子模块的输出电压,使得在交流侧得到所期望的多电平电压输出,同时在直流侧得到约等于Udc的电压值,这就是MMC的基本控制原则[3]。
上下桥臂间电压比率的调节,即Nu、N1的调节是通过T1、T2不同开关状态实现的:
1)T1、T2都闭锁,这时系统处于初始启动状态或故障状态;2)T1导通,T2闭锁,子模块电容通过T1放电或通过反向二极管D1充电,这取决于流过子模块电容的电流方向,此时其输出电压为,Uc,Nu增大或 N1增大;3)T1 闭锁,T2 导通,电流通过T2或反向二极管D2流通,子模块电容被旁路,此时输出电压为0,Nu减小或N1减小。
如此,当一个桥臂投入的模块从0~N变化,另一桥臂投入模块数从N~0变化时,AC侧可得到N+1电平电压输出。
2 基于同步发电机模型的MMC并网控制策略
2.1 控制策略
假设采用的同步发电机模型为理想模型[8,9],即转子为圆形,无阻尼绕组,每相有1对磁极,铁芯没有饱和效应;定子三相绕组结构相同,旋转对称,空间相隔120°电角,可看成自感系数为L,互感系数为M的集中线圈。该理想电机模型对电力系统的暂态与动态分析已经足够精确,能满足电力系统分析的需要。其具体结构如图3所示。
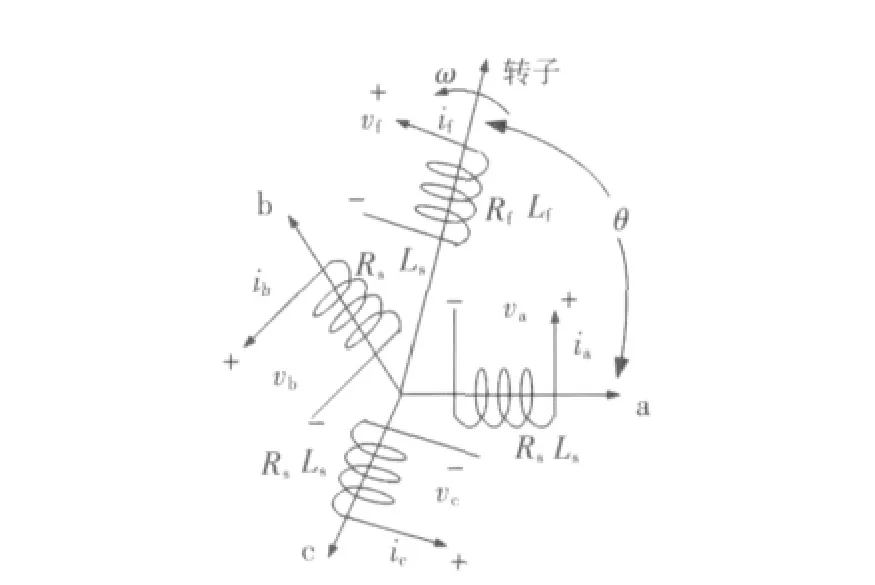
图3 理想同步发电机结构Fig.3 Structure of idealized synchronous generator
由同步发电机的力学方程:

可知转子转动的角θ为
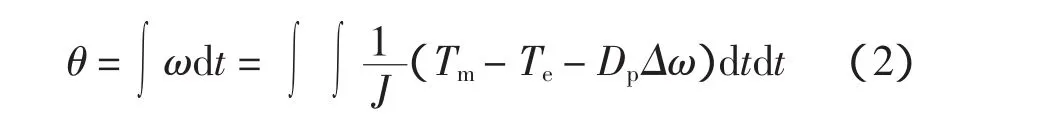
式中:J为转子转动惯量;Tm为机械转矩;Te为电磁转矩;ω为转子的角速度;则定子线圈与转子线圈之间的互感为
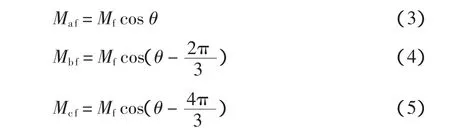
定子各线圈的磁通量为
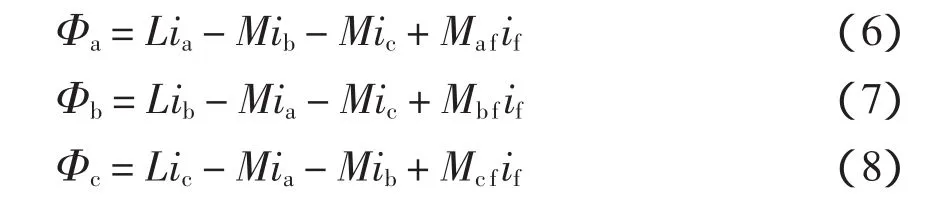
式中:ia、ib、ic为定子相电流;if为转子励磁电流。此模型不需要励磁电压,采用可调节的恒定励磁电流来调节输出端电压。
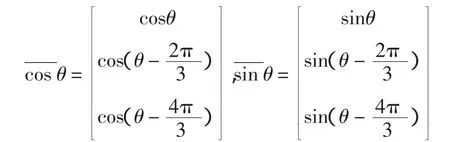
则定子线圈磁通量可写为

式中,Ls=L+M。
令定子线圈阻抗为Rs,相端电压为v且有

则由式(9)可得
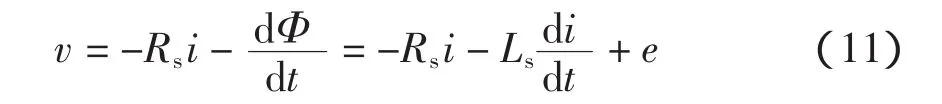
其中e=[eaebec]T为转子转动产生的感应电势,由式(9)和式(11)可得
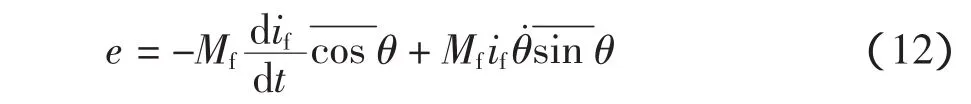
由于if是可调节的直流电流源,则式(12)可改为

将式(11)中的Rs、Ls看作MMC输出端连接的电阻和电感,那么将e信号进行处理后即可作为MMC 的调制信号 m(t)。
在MMC控制中,MMC输出电压与直流侧电压的关系式为

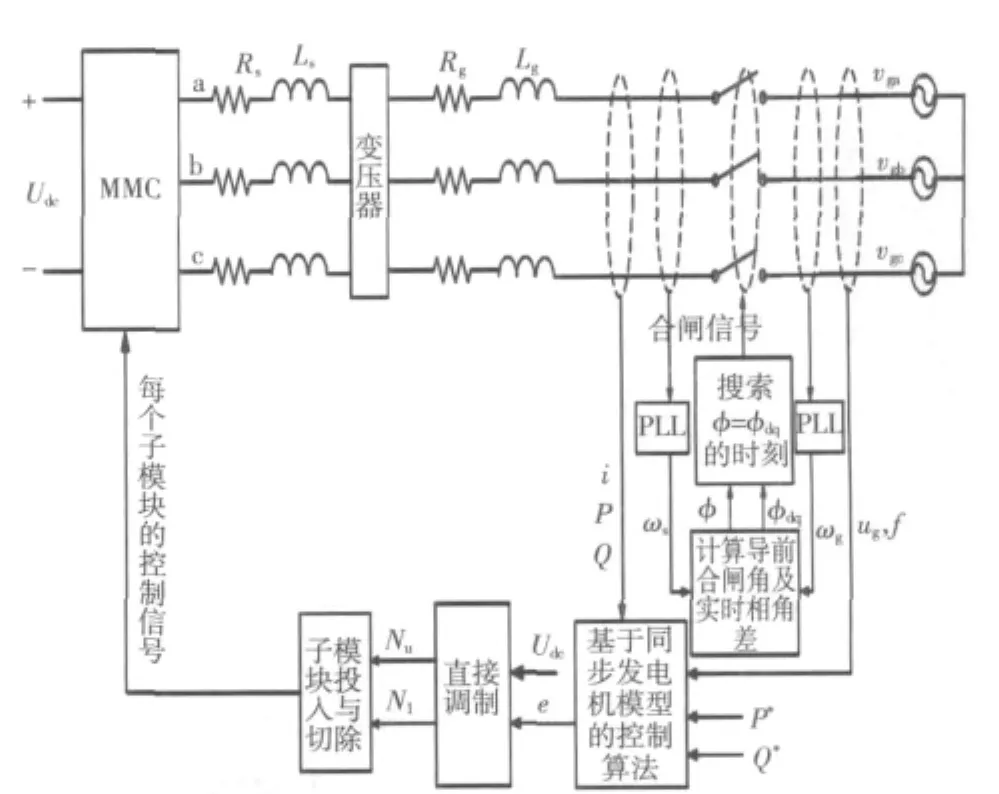
图4 基于同步发电机模型的MMC并网控制框图Fig.4 Grid-connected diagram of MMC based on model of synchronous generater
式中,Udc为直流侧输入电压。
根据MMC控制的直接调制方式[4]可得MMC每相上下桥臂投入的模块数分别为
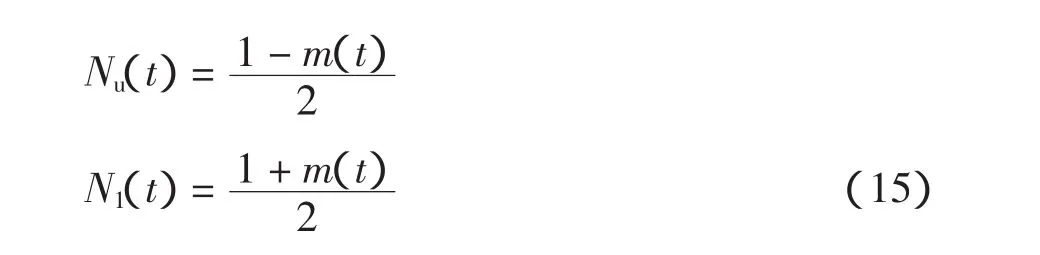
得到了上下两桥臂需投入的模块数,则按照第1节中所介绍的控制原则对MMC进行控制,即可得到所希望的电压输出。
2.2 并网方式
基于同步发电机模型控制MMC可以使得MMC输出具有类似同步发电机的特性[8],因此在该控制策略下可采用同步发电机的准同步思想实现MMC并入电网。准同步是一种冲击很小的并网方式,它是在待并发电机与电网的频差和压差小于一定值时,在零相差到来前相当于待并发电机断路器合闸时间的时刻给出合闸信号,使发电机平滑并入电网,这也就是所谓的恒定导前时间准同步思想[10]。
要确定何时合闸将MMC并入电网,首先要计算出导前合闸角,其计算公式为
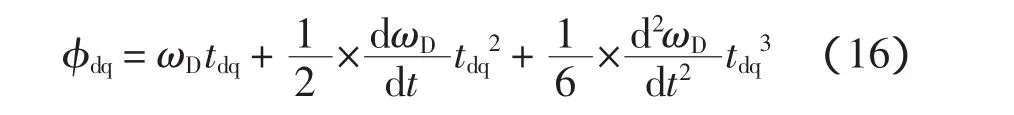
式中:ωD为待并MMC侧与电网侧的角频率差;tdq为导前时间,即断路器合闸回路动作时间。在计算出了理想导前合闸角φdq后,将其与实时相角差φ比较,不断搜寻φ-φdq=0的时机,一旦出现,控制器即发出合闸信号,使待并MMC恰好在相角差φ=0的时刻并入电网。
基于同步发电机模型的MMC并网控制框图如图4所示。
3 仿真试验
3.1 基于同步发电机模型的MMC并网
在MATLAB/Simulink平台上搭建MMC模型,对上述基于同步发电机模型的MMC并网控制策略进行仿真[11-12],该仿真采用同步发电机的准同步并网方式并网,系统仿真结构如图4所示。MMC每相由20个子模块组成,上下桥臂各10个。MMC直流侧电压Udc=700 V,交流侧电路参数为:Rs=1 Ω,Ls=3 mH,Rg=1 Ω,Lg=10 mH,tdq=50 ms,电网电压有效值为220 V。
图5所示为基于同步发电机模型控制MMC并网时的合闸控制信号,用Uctul表示。从图中可以看出,控制系统发出合闸控制信号的时刻为0.32 s,而断路器合闸回路动作时间tdq为50 ms,则MMC真正并入电网的时刻为0.37 s。
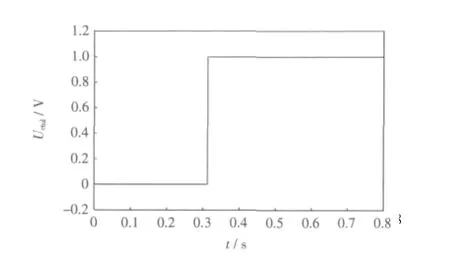
图5 合闸信号Fig.5 Switching signal
图6所示为基于同步发电机模型控制MMC并网时MMC输出a、b、c三相电流跟踪电压相位情况,其中实线为电网电压标幺值,虚线为MMC输出电流标幺值,从图中可以看出,0.37 sMMC并入电网后经过3个半周期a、b、c三相电流就可分别跟踪上相应的电网电压相位,并且幅值能够达到其标幺值,即MMC输出功率已达到给定值。
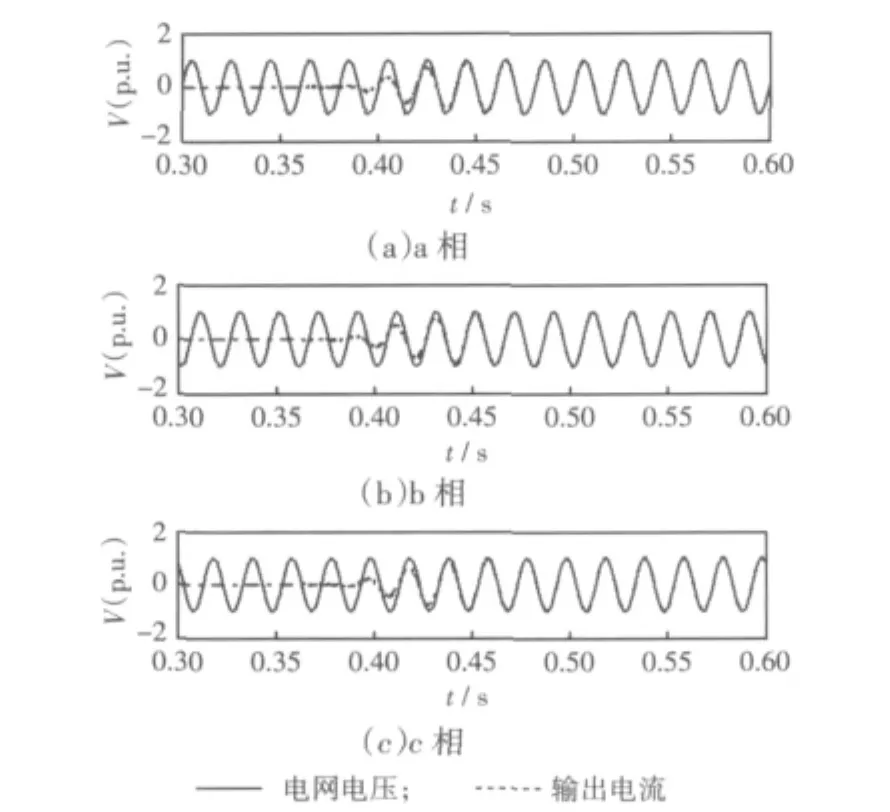
图6 基于同步发电机模型控制MMC并网电流跟踪电网电压Fig.6 Output currents of MMC controlled by model of synchronous generater track phase of grid voltage
3.2 PI控制MMC并网
基于3.1小节中搭建的MMC模型,对PI控制其并网电流跟踪电网电压相位的控制方法进行仿真,该仿真采用电流型并网方式,即在系统运行之前先将MMC连到电网,然后启动控制系统调节MMC输出电流跟踪电网电压相位。其控制框图如图7所示。
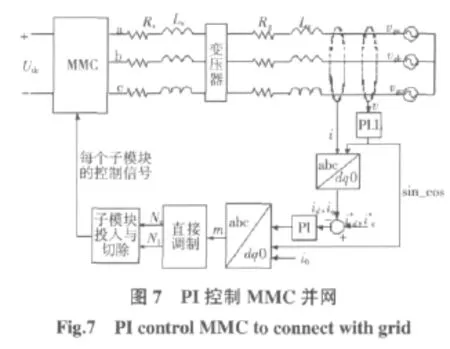
其中MMC的结构和参数、直流侧参数以及交流侧参数都与3.1小节仿真中的参数一致,根据逆变器并网时电流环控制并网电流的经典方法计算PI参数,再根据经验值稍作调整得Kp=0.1,Ki=20。仿真结果如图8所示。
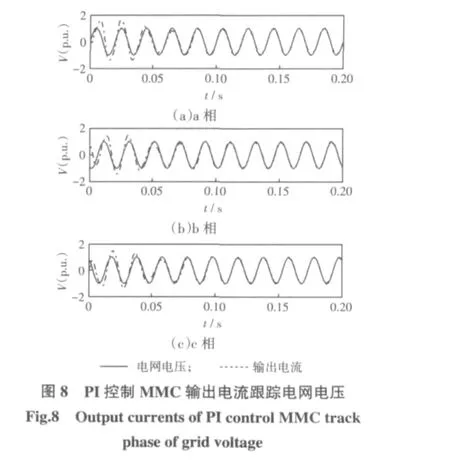
图8所示为PI控制MMC并网时电流跟踪电压相位情况,其中实线为电网电压标幺值,虚线为MMC输出电流标幺值,从图中可以看出,a、b、c三相电流都跟踪上相应电压相位,并且幅值达到标幺值需要5个周期的时间。由图6和图8比较可知,前者的电流在MMC并入电网后快速平滑增长,这也就意味着MMC的并网过程是快速平滑的,并且并网冲击很小;后者的电流则需经过一段时间大幅值波动之后才能达到既定目标,而此时的MMC早已与电网相连,该电流波动势必会对电网产生较大冲击。由此可知,基于同步发电机模型控制MMC并网具有明显优势,它既可以保证MMC输出电流快速跟踪电网电压相位,并达到给定值,实现功率因数为1,也可以使MMC平滑并入电网,并且并网冲击很小,实现友好并网。
4 结语
本文将同步发电机模型及同步发电机的准同步并网方式应用于MMC并网控制,并对控制系统进行了公式推导,在MATLAB/Simulink平台上搭建了MMC模型,完成了基于同步发电机模型控制MMC并网和PI控制MMC并网仿真,并对两者的仿真结果进行了比较。比较结果表明,基于同步发电机模型的MMC并网比PI控制MMC并网更具有优势,前者既可以使MMC输出电流更快速、准确的跟踪电网电压相位,实现并网功率因数为1,也能够使MMC平滑、小冲击并入电网,实现友好并网。
[1]黄汉奇,毛承雄,王丹,等(Huang Hanqi,Mao Chengxiong,Wang Dan,et al). 可再生能源分布式发电系统建模综述(Modeling summarizing of distributed renewable energy power generation system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(5):1-18,24.
[2]刘钟淇,宋强,刘文华(Liu Zhongqi,Song Qiang,Liu Wenhua).基于模块化多电平变流器的轻型直流输电系统(VSC-HVDC system based on modular multilevel converters)[J].电力系统自动化(Automation of Electric Power Systems),2010,34(2):53-58.
[3]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2010.
[4]Marquardt R,Lesnicar A.New concept for high voltagemodular multilevel converter[C]//IEEE Power Electronics Specialists Conference.Aachen,Germany:2004.
[5]Vasiladiotis M.Analysis,Implementation and Experimental Evaluation of Control Systems for a Modular Multilevel Converter[D].Sweden:Department of Electrical Engineering of Royal Institute of Technology,2009.
[6]刘钟淇,宋强,刘文华(Liu Zhongqi,Song Qiang,Liu Wenhua).新型模块化多电平变流器的控制策略研究(Research on control of the novel modular multilevel converters)[J].电力电子技术(Power Electronics),2009,43(10):5-7,18.
[7]Dorn J,Huang H,Retzmann D.Novel voltage source converters of HVDC and FACTS applications[C]//CIGRE International Symposium Conference.Osaka,Japan:2007.
[8]Zhong Qing-Chang,Weiss G.Synchronverters:inverters that mimic synchronous generators[J].IEEE Trans on Industrial Electronics,2011,58(4):1259-1267.
[9]房大中,贾宏杰.电力系统分析[M].北京:科学出版社,2010.
[10]卓乐友,叶念国,翁乐阳,等.微机型自动准同步装置的设计与应用[M].北京:中国电力出版社,2002.
[11]徐敏,彭瑜(Xu Min,Peng Yu).MATLAB在《电力系统分析》教学中的应用(Applications of MATLAB in teaching of
[12]程军照,李澍森,张腾飞(Cheng Junzhao,Li Shusen,Zhang Tengfei).多路并网光伏发电系统的仿真与分析(Simulations and analysis on a multi-branch grid-connected photovoltaic system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):58-62.
