基于自动微分技术的VSC-HVDC潮流计算

季 聪，卫志农，孙国强，韦延方

（河海大学可再生能源发电技术教育部工程研究中心，南京 210098）

随着新型电力电子器件的出现特别是全控型器件的发展，基于电压源换流器VSC（voltage source converter）和脉宽调制PWM（pulse width modulation）控制技术的新一代高压直流输电——VSC-HVDC（voltage source converter based high voltage direct current）已经成为现实。1997年投入运行的瑞典Hellsjon实验性工程是世界上第一个采用VSC的直流输电工程。此工程的意义在于，它首次实现VSC-HVDC技术的工程化应用，使直流输电进入了一个新的发展阶段，开创了直流输电技术的新时代。我国第一条VSC-HVDC示范工程——上海南汇风电站系统于2011年5月并网成功，整体投入试运行，标志着我国具有自主知识产权的VSC-HVDC核心技术成功应用于实际工程。作为新一代直流输电技术，VSC-HVDC解决了常规直流输电技术的许多固有技术瓶颈：它可以无需无功补偿实现有功功率和无功功率的独立控制；可以用于对无源系统供电，而无需电网短路电流的支撑换相；滤波容量小、占地面积小。因此VSC-HVDC成为近年来众多学者研究的热点[1-4]。

在含VSC-HVDC的交直流潮流计算[5-8]中，形成雅克比矩阵采用的是最直接的方法，即手工对功率不平衡函数的表达式进行微分，然后编写微分代码。由于加入VSC-HVDC后系统变量增加，编写代码的过程变得繁琐，工作量变大而且易于出错，自动微分 AD（automatic differentiation）技术的出现克服了这个缺点。AD将微分定义为代数运算，它可以计算任意阶微分。目前AD技术已经在电力系统潮流计算，状态估计及最优潮流等方面得到了应用[9-11]。

目前采用的统一迭代法（下称统一法）求解交直流混合系统的潮流计算方法是在传统潮流计算方法的基础上扩展形成的。该算法收敛性好，但对原有的纯交流程序继承性差，代码编制工作量大，而采用AD可以很大程度上克服这些缺点，提高代码编写效率，缩短程序开发周期。

但AD的引入增加了计算时间，故本文提出了一种定雅克比矩阵的保留非线性方法，使调用AD产生的时间损失大大降低，同时该算法的计算量也远小于统一迭代法。

本文着重研究AD技术在含VSC-HVDC交直流潮流计算中的应用。结合AD技术，将基于运算符重载的 ADOL-C（automatic differentiation by overLoading in C++）自动微分工具应用于统一法交直流潮流计算和保留非线性的潮流计算。实践表明，用AD技术代替传统的手工编写微分代码计算Jacobian矩阵，使代码量大大缩减，减少了程序的开发周期；而算例结果表明，保留非线性潮流算法计算量更小，计算速度更快，即使是采用了AD技术以后，在计算速度上依然有着明显的优势。

1 AD技术

1.1 基本原理

微分运算一直是目标优化、非线性系统求解、灵敏度分析等热点课题中的关键技术之一。1961年Robinson引入“无穷大量”和“无穷小量”，建立了“非标准分析”理论，提出在实数的延拓空间中，微分可以定义为代数运算。这种思想同计算机技术相结合就形成了“自动微分技术”[13，14]。

对AD技术而言，无论函数多么复杂，总是由一系列的基本操作组成，如四则运算（加、减、乘、除），基本函数（三角函数、指数函数、对数函数等）。下面举例说明：

将式（1）所示的函数引入到独立变量和中间变量分解成一系列的基本运算，如表1所示。

表1 独立变量和中间变量Tab.1 Independent and intermediate variables

由此在已知独立变量的值之后，自顶而下就可以得到函数的精确值y。

给定x˙1、x˙2，通过使用微分计算的链式法则，AD技术可以以完全机械的方式得到函数的微分，而且不含截断误差。目前AD有两种模式：正模式和逆模式，它们的区别在于运用链式法则计算传递函数的方式不同。

正模式直接按照表2自上而下，传递中间变量关于独立变量的导数，求得函数的导数。逆模式具体流程见文献[10]。

表2 正模式Tab.2 Forward modes

1.2 AD工具

现存的两种自动微分的实现方法：源代码变换方法和运算符重载方法。源代码变换是显式的重写源代码以得到导数代码的方法，代表软件有ADIFOR和ADIC。运算符重载利用C++等高级语言中的操作符重载的机理，通过重载每个操作以达到计算偏导数和根据链式法则传递导数的目的，代表软件有ADOL-C和ADC。

ADOL-C是由Dresden技术大学科学计算学院开发的自动微分系统，使用运算符重载的方法对C++程序进行自动微分，能够以正模式和逆模式计算任意阶导数。基于以上优点，本文选择ADOLC工具进行微分计算

2 VSC-HVDC稳态模型

2.1 VSC-HVDC稳态特性

交直流系统由交流系统和直流系统组成，其接口如图1所示。

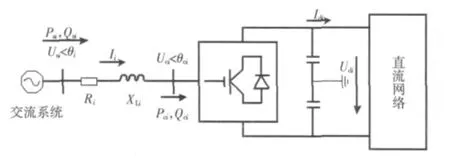
图1 VSC-HVDC模型Fig.1 Model of VSC-HVDC

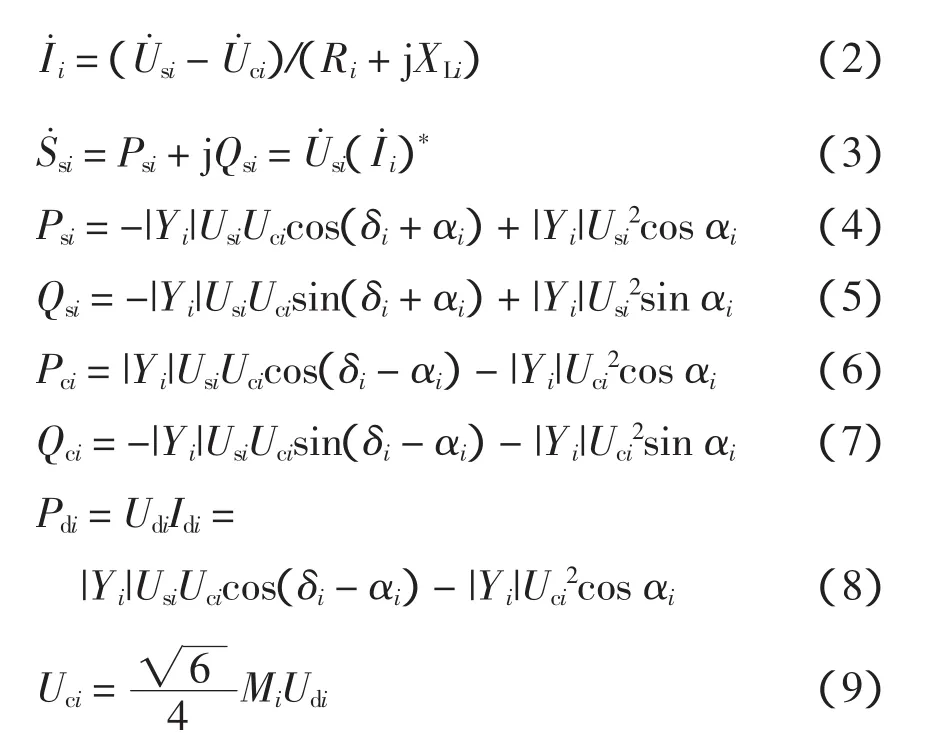
方程（2）～（9）则构成了标幺制下 VSC-HVDC的稳态潮流计算模型。具体推导过程和变量说明见文献[12]。

2.2 VSC-HVDC的控制方式

VSC-HVDC中VSC可以选择的控制方式有以下几种[7]：①定直流电压、定无功功率控制；②定直流电压、定交流电压控制；③定有功功率、定无功功率控制；④定有功功率、定交流电压控制。

本文对直流支路两端的VSC-HVDC采用以下四种控制方式组合：①+③；①+④；③+②；④+②。

2.3 潮流方程

对于系统中的纯交流节点，其潮流计算方程为

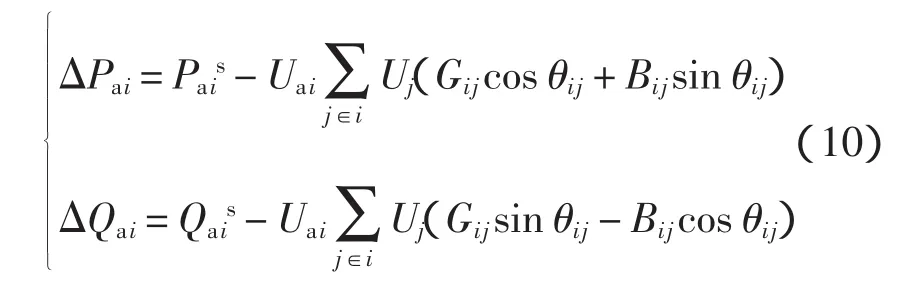
对于直流节点，其潮流计算方程为

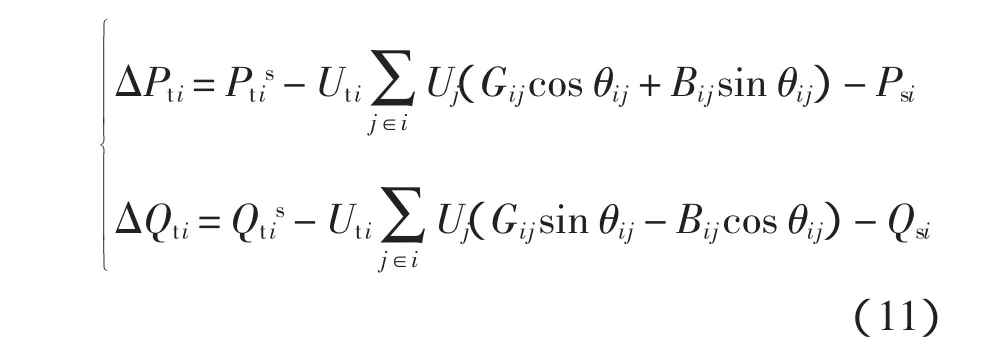
根据VSC-HVDC的稳态模型，可得到直流系统的潮流计算方程为

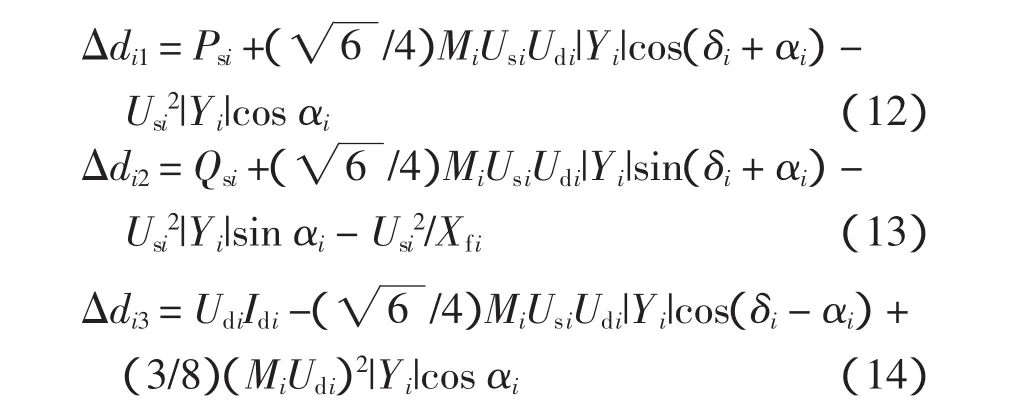
式中，下标i表示第i个VSC。

直流网络的电流偏差量方程为

式中，gdij为直流节点i、j之间的电导值。

在交直流潮流中融入AD技术后，与手动编程的区别在于，它将需要求解的变量声明为ADOL-C的一组活跃变量，并用这一组活跃变量将系统的潮流方程表达出来，再调用函数库中的Jacobian函数，生成系统的雅克比矩阵。

3 AD技术在交直流潮流中的应用

在交直流潮流中融入AD技术后，与手动编程的区别在于，它将需要求解的变量声明为ADOL-C的一组活跃变量，并用这一组活跃变量将系统的潮流方程表达出来，再调用函数库中的Jacobian函数，生成系统的雅克比矩阵。

3.1 AD在统一迭代法交直流潮流中的应用

统一迭代法需要在每次循环中根据迭代得到的系统变量值更新Jacobian矩阵，故每次循环都需要调用AD产生新的Jacobian矩阵，具体步骤如下，流程如图2所示。

步骤2 声明活跃变量数组X，并将x的值赋给X；

步骤3 初始化，迭代次数k置1；

步骤4 声明活跃变量F，用活跃变量X写出不平衡量F的表达式，将F的数值传递给f；

步骤6 调用ADOL-C的Jacobian函数计算Jacobian矩阵；

步骤7 三角分解法求得Δx(k)；

步骤 8 置k=k+1，x(k+1)=x(k)+Δx(k)，转步骤5。

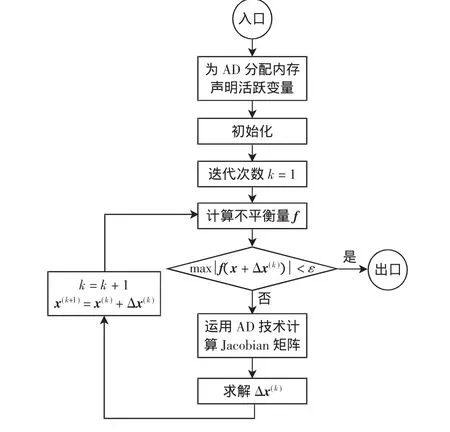
图2 运用AD技术的统一法交直流潮流程Fig.2 Flow chart of simultaneous method AC-DC system power flow with AD technology

3.2 AD在保留非线性法交直流潮流中的应用

保留非线性法保留了泰勒表达式的高阶项，其Jacobian矩阵恒定，故只需在迭代之前，根据初值计算出Jacobian矩阵即可，整个计算过程中只需调用一次AD技术，故AD的引入将基本不会影响计算速度，算法的数学描述见文献[15]。基于AD的保留非线性法交直流潮流步骤如下，流程如图3所示。

步骤 1 设定初值 x={U，θ，Ud，Id，δ，M，Ps，Qs}；

步骤2 声明活跃变量数组X，并将x的值赋给X；

步骤3 初始化，迭代次数k置1；

步骤4 声明活跃变量F，用活跃变量X写出潮流方程F的表达式，将F的数值传递给f；

步骤5 调用ADOL-C的Jacobian函数计算Jacobian矩阵；

步骤 8 置 k=k+1，x(k+1)=x(k)+Δx(k)，转步骤6。

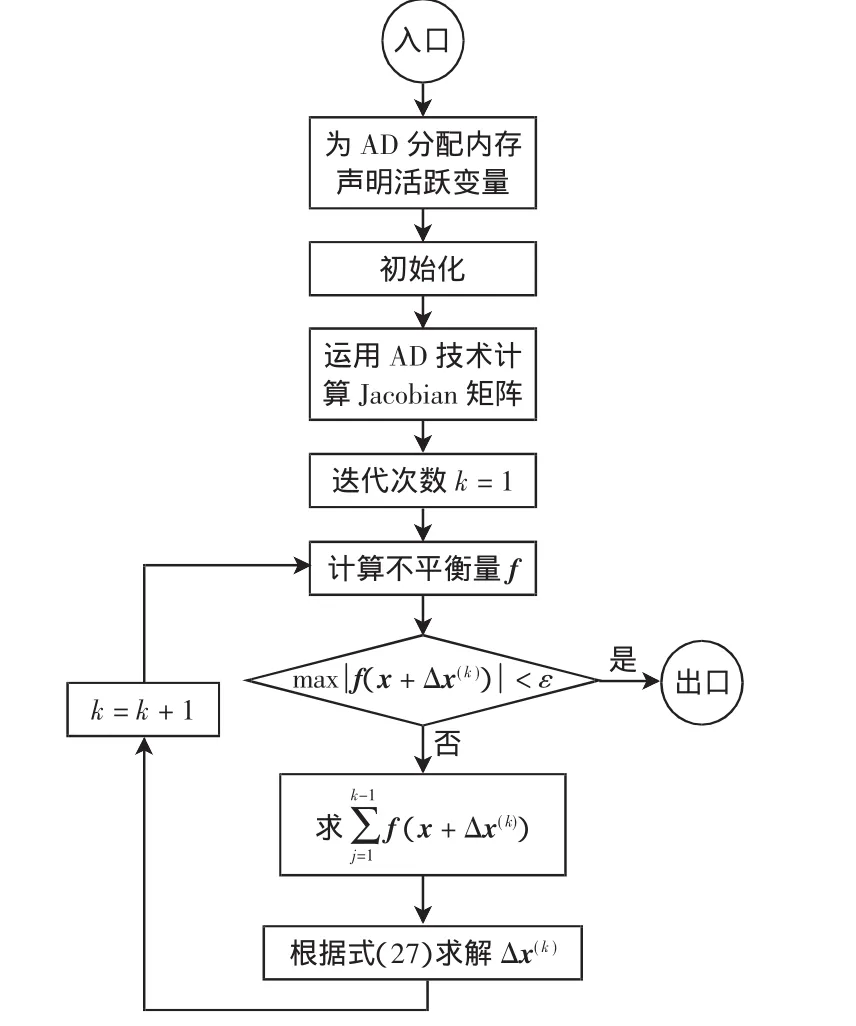
图3 运用AD技术的保留非线性法交直流潮流程Fig.3 Flow chart of retaining nonlinearity method AC-DC system power flow with AD technology

4 算例分析

4.1 基本算例测试

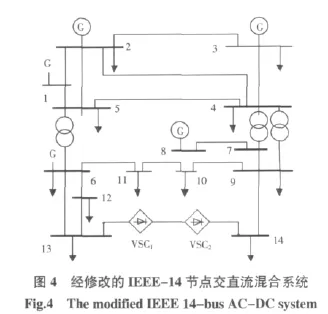
下面以经修改的IEEE14节点系统为例，验证上述算法的有效性。

图4为将IEEE-14节点系统的13-14支路替换为直流支路，并在交流节点接入VSC装置后得到的交直流系统。直流系统参数如表3所示，均为标幺值。

其中NBUS表示VSC所在的母线号，P1、Q1为VSC所在母线连接的负荷有功、无功，U、θ表示VSC所在母线的交流电压幅值、相角，Ps、Qs为直流系统的注入有功、无功，Ud为直流电压。R、X、XL、P1、Q1由系统给定；Ps、Qs初值设为与修改前系统支路功率相等，由原系统的潮流计算得到。Id、δ、M、分别为

表3 直流系统参数Tab.3 DC system parameters

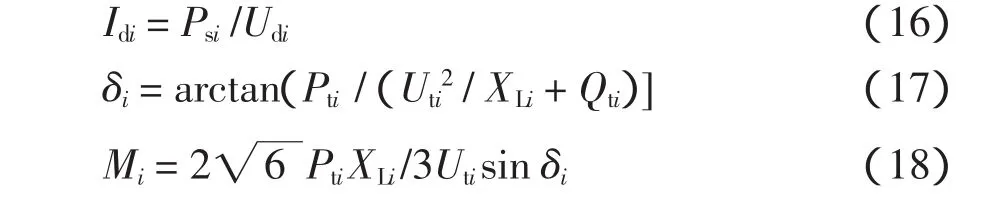
式中，Pgi为节点发电有功。

表4和表5列出了经修改的IEEE14节点系统在手动编程和基于AD技术两种方式下的统一法和保留非线性法潮流计算结果，方法A、方法B为手动编程的统一法和保留非线性法，方法C、方法D为基于AD技术的统一法和保留非线性法，平均电压单位为标幺值。由于手动编程和基于AD技术的潮流计算结果并无差异，故表4只列出A、C两种方法的计算结果。表5中除单位为度（°）外，其他均为标幺值。

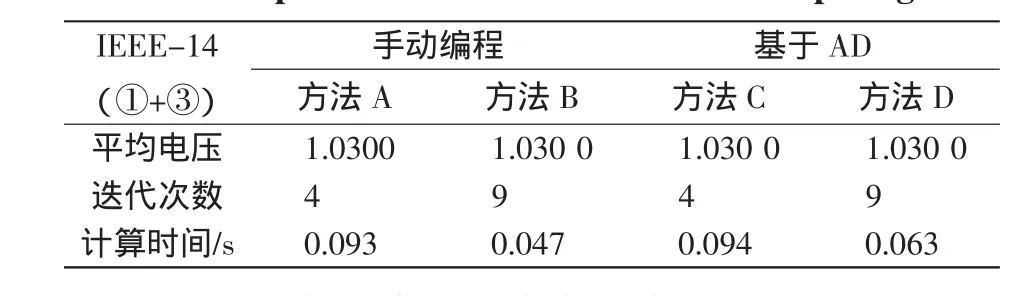
表4 迭代次数和计算时间比较Tab.4 Comparison of iteration times and computing time

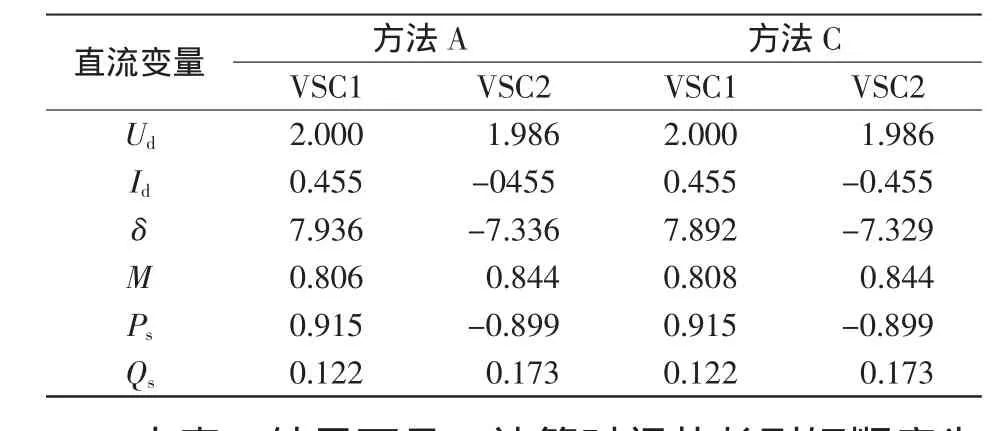
表5 各VSC控制及状态变量Tab.5 VSC control and state parameters

由表4结果可见，计算时间从长到短顺序为方法A、方法C、方法B、方法D。采用AD后统一法所需计算时间增加，而保留非线性方法在手动编程和基于AD技术两种方式下速度均优于统一迭代法。

4.2 控制模式测试

在实际电力系统运行中，为了实现稳定运行、减少损耗、控制潮流等功能，VSC-HVDC常常需要在多种控制模式下运行。

表6列出了在不同控制方式下，手动编程的统一迭代法和保留非线性法的收敛次数和计算时间比较。

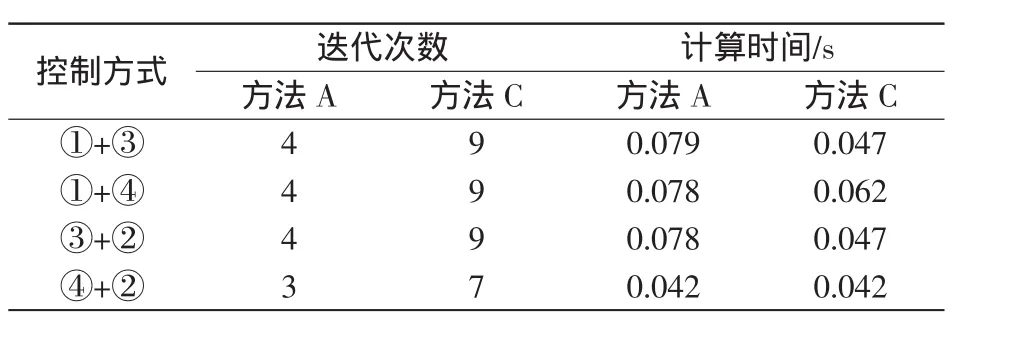
表6 不同控制方式下计算结果比较Tab.6 Computational results comparison in different control modes

由此可知，不同控制方式下，统一法和保留非线性方法均能很快收敛，而且保留非线性方法速度上一直占有比较大的优势。

4.3 算法效率测试

表7列出了统一法、保留非线性算法对系统进行计算的迭代次数和计算时间，各系统直流支路两端的VSC控制方式组合为①+③。

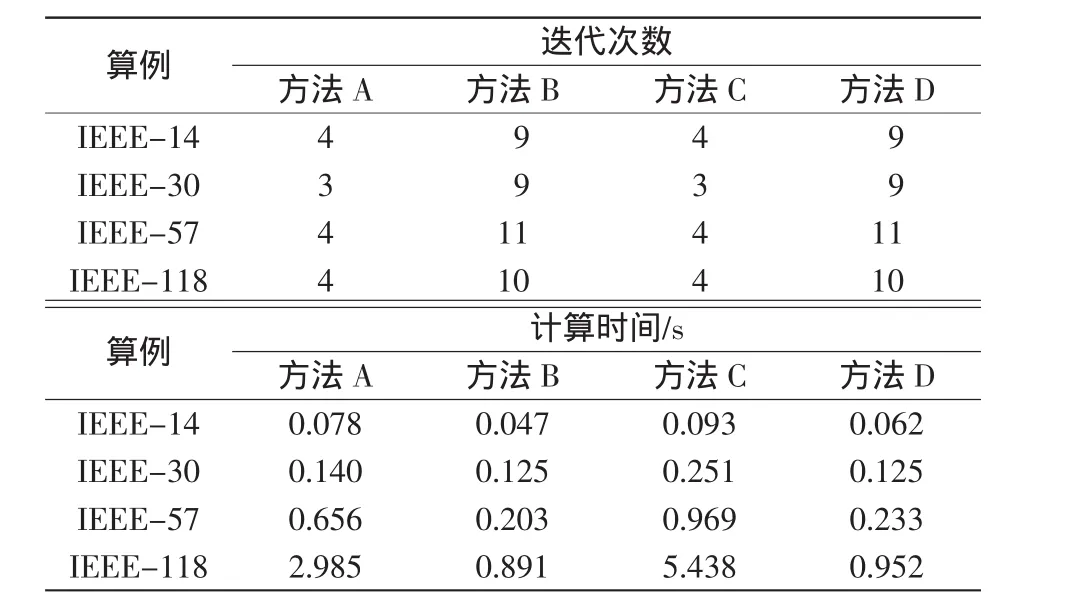
表7 各算例迭代次数和计算时间比较Tab.7 Iteration times and computing time comparison of different test systems

表中多个算例结果表明，在手动编程写Jacobian矩阵时，保留非线性方法较统一迭代法速度更快，而采用AD技术后，保留非线性方法由于只需要生成一次Jacobian矩阵，并只需对其进行一次三角分解，大大减少了计算量，缩短了计算时间。表中算例结果表明，系统越大，保留非线性方法在速度上的优势越明显。

5 结论

（1）将AD技术引入到统一迭代法的VSCHVDC潮流计算中，验证了AD技术的有效性。

（2）将保留非线性方法用于含VSC-HVDC的交直流潮流计算，并验证了其在速度上的优越性。

（3）在修改后的 IEEE-14、30、57、118 节点系统上，基于AD技术，进行了含VSC-HVDC的交直流混合系统潮流的算例仿真和分析，仿真结果验证了AD技术有效性和保留非线性方法的优越性。

[1]李庚银，吕鹏飞，李广凯，等（Li Gengyin，Lü Pengfei，Li Guangkai，et al）.轻型高压直流输电技术的发展与展望（Development and prospects for HVDC light）[J].电力系统自动化（Automation of Electric Power Systems），2003，27（4）：77-81.

[2]汤广福，贺之渊，腾乐天，等（Tang Guangfu，He Zhiyuan，Teng Letian，et al）.电压源换流器高压直流输电技术最新研究进展（New progress on HVDC technology based on voltage source converter）[J].电网技术（Power System Technology），2008，32（22）：39-44，89.

[3]袁旭峰，程时杰（Yuan Xufeng，Cheng Shijie）.多端直流输电技术及其发展（Multi-terminal HVDC transmission technology and its development）[J].继电器（Relay），2006，34（19）：61-67，70.

[4]陈蔓，陆继明，毛承雄，等（Chen Man，Lu Jiming，Mao Chengxiong，et al）.基于遗传算法的优化控制在VSCHVDC中的应用（Application of genetic algorithm based optimal control in VSC-HVDC）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（4）：19-23.

[5]陈谦，唐国庆，王浔（Chen Qian，Tang Guoqing，Wang Xun）.多端VSC-HVDC系统交直流潮流计算（AC-DC power flow algorithm for multi-terminal VSC-HVDC systems）[J].电力自动化设备（Electric Power Automation E－quipment），2005，25（6）：1-6.

[6]Angeles-Camacho C，Tortelli O L，Acha E，et al.Inclusion of a high voltage DC-voltage source converter model in a Newton-Raphson power flow algorithm[J].IEE Proceedings-Generation，Transmission and Distribution，2003，150（6）：691-696.

[7]郑超，周孝信，李若梅，等（Zheng Chao，Zhou Xiaoxin，Li Ruomei，et al）.VSC-HVDC 稳态特性与潮流算法的研究（Study on the steady characteristic and algorithm of power flow for VSC-HVDC）[J].中国电机工程学报（Proceedings of CSEE），2005，25（6）：1-5.

[8]Zhang Xiaoping.Multiterminal voltage-sourced converter-based HVDC models for power flow analysis[J].IEEE Trans on Power Systems，2004，19（4）：1877-1884.

[9]Orfanogianni T，Bacher R.Using automatic code differentiation in power flow algorithms[J].IEEE Trans on Power Systems，1999，14（1）：138-144.

[10]叶芳，卫志农，孙国强，等（Ye Fang，Wei Zhinong，Sun Guoqiang，et al）.基于自动微分技术的电力系统状态估计算法（State estimation of power systems with automatic differentiation technology）[J].电力系统保护与控制（Power System Protection and Control），2010，38（17）：91-95，100.

[11]耿光超，江全元（Geng Guangchao，Jiang Quanyuan）.基于自动微分技术的内点法最优潮流算法（An automatic differentiation based interior-point method for optimal power flow）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（23）：41-45.

[12]孙国强，李育燕，卫志农，等（Sun Guoqiang，Li Yuyan，Wei Zhinong，et al）.含 VSC-HVDC 的交直流混合系统状态估计（State estimation of power system with VSCHVDC）[J].电力系统自动化设备（Electric Power Automation Equipment），2010，30（9）：6-12，23.

[13]Walther A，Griewank A.A package for the automatic differentiation of algorithms written in C/C++[EB/OL].http：//www.coin-or.org/projects/ADOL-C.xml，2009.

[14]王莉萍，程彬杰，唐天同，等（Wang Liping，Cheng Binjie，Tang Tiantong，et al）.用于电子光学系统像差分析的自动微分技术及其在Visual C++平台上的软件实现（Automatic differentiation technique for aberration analysis of electronic optic systems with implementation in Visual C++environment）[J].电子显微学报（Journal of Chinese Electron Microscopy Society），1999，18（6）：644-651.

[15]王宪荣，柳焯，张伯明（Wang Xianrong，Liu Chao，Zhang Boming）.非线性总项与保留非线性潮流算法的拓广（The sum total of nonlinear terms and the development of load flow algorithm retaining nonlinearity）[J].哈尔滨工业大学学报（Journal of Harbin Institute of Technology），1990，22（6）：60-66.

[16]陆进军，黄家裕（Lu Jinjun，Huang Jiayu）.电力系统多端直流（MTDC）潮流算法改进（An improved multi-terminal HVDC power flow method）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2000，12（5）：4-6，18.

[17]吴素平，尚荣艳，罗隆福（Wu Suping，Shang Rongyan，Luo Longfu）.新型直流输电系统中感应滤波技术的影响（Impacts of inductive filtering technology in the novel DC transmission system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（4）：49-55.