基于前景理论的电动汽车多模式充电行为分析
2013-07-02刘继春党小强
冯 艾,刘继春,吴 磊,党小强
(1.四川大学电气信息学院,智能电网四川省重点实验室,成都 610065;2.克拉克森大学电气与计算机工程系,纽约 13699-5720;3.四川大学水电学院,成都 610065)
电动汽车以其高效能、低排放,削峰填谷,提供旋转备用,增加新能源消纳的能力等诸多优点引起各国政府的高度关注。作为一类负荷,电动汽车的接入对电网将造成影响,因而对其充电功率预测的探讨至关重要。
目前,已有不少学者对电动汽车充电行为进行了研究。文献[1]分析电池的特点:容量、续航里程、充电时间、循环使用次数,说明不同类型的电池其充电功率有明显的不同,却未对电动汽车的需求充电功率进行建模。文献[2-3]对电动汽车的功率进行建模,没有探讨初始荷电状态分布的影响。文献[4]电功率的影响,未考虑充电抉择行为的影响。文献[5]以电池寿命最佳和能源消耗最小为目标,求解电动汽车电池最优充电方案,却忽略了电池使用成本及充电电价对电池充电方案的影响。文献[6]考虑外部电网约束对充电功率的影响,但没考虑电动汽车自身使用特性对充电功率的影响。文献[7]研究了电价政策对电动汽车充电时间选择的影响,却没有对低谷时段电动汽车的充电模式进行分析。
本文运用前景理论分析了电动汽车充电的抉择行为,定义了电动汽车充电抉择的临界决策点;求解了基于临界决策点、起始充电时刻和起始荷电状态分布的不受控制充电模式下的电动汽车充电功率曲线;构建了控制充电方案下电动汽车的充电功率模型,基于遗传算法求解了最优控制方案下电动的充电方案和功率曲线。
1 电动汽车充电抉择分析
根据电动汽车的使用情况,并不是所有的电动汽车在低谷时段都需要充电;并且在电动汽车电池电量比较多的情况下充电,将降低电池的使用寿命[5]。当然为了满足次日电动汽车出行的需要,一些电动汽车的电池确实需要进行充电。为此,本文采用前景理论[8]对电动汽车是否选择充电这一行为进行分析。
运用前景理论分析步骤如下:
(1)确定各决策备选方案可能引起的费用;
(2)选择“参照点”,计算各备选方案可能带来的“收益”和“损失”;
(3)根据Kahneman价值函数计算各“收益”和“损失”的价值大小;
(4)根据Kahneman权重函数计算权重大小;
(5)根据前景值函数计算各备选方案下的前景值;
(6)根据前景值做抉择,确定临界决策点。
1.1 电动汽车充电决策造成的费用
电动汽车充电决策造成的费用有额外成本费用和额外充电费用。额外成本费用:是指当低谷时段选择充电时,可能造成电动汽车电池因不必要充电而引起的额外的电池成本流失的费用。额外充电费用:其是指当选择低谷时段不充电时,电动汽车可能获得因在外进行快速充电而额外多支付的充电费用。
假设电动汽车电池的使用寿命为n1次,单体电池的总花销费用为CB元;假设电池每次充电造成的电池固定成本流失的费用是一样的,则额外成本费用Ff为

设在家充电的电价为CS元/kw·h,一次满充的需求充电电量为Q0kW·h,在外快速充电的电价为Cq元/kW·h,则额外充电费用Fe为

1.2 充电决策的“收益”和“损失”
当选择既不获取收益也不希望损失作为决策的“参照点”时,则充电决策可能造成的“收益”或“损失”为

其中,σ为0或1的变量,且满足:

1.3 “收益”或“损失”的价值计算
在面对收益和损失时,前景理论认为同等数量的收益和损失给人的感觉是不一样的,即它们的效用值不同。其用价值函数来求解,即
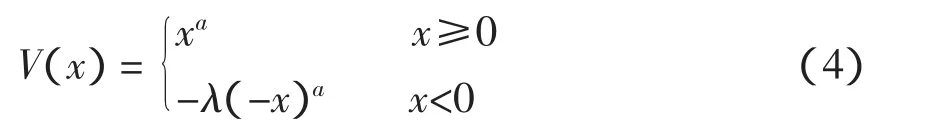
式中:a表示收益和损失区域价值函数的凹凸程度;λ表示损失区域与收益区域的比值。通常取值为 α=0.88,λ =2.25,由 Kahneman标定。
1.4 权重值的求解
假设事件结果为x的事件的概率为p,运用权重函数求解其权重值,其求解公式为
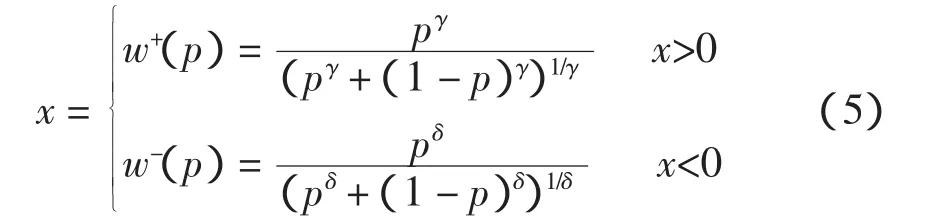
其中,γ =0.16,δ=0.69,由 Kahneman 标定[8]。
1.5 各方案下前景值的计算
电动汽车充电行为事件结果概率分析。任意初始荷电状态下,电动汽车选择不充电方式时,其收益的概率为剩余电量能满足次日的行驶需求的概率;其产生损失的概率为剩余电量不能满足次日的行驶需求的概率。设初始荷电状态下,电动汽车的剩余可行驶里程为l0km,电动汽车日行驶里程概率密度函数为fX(x),日最大行驶里程为S km则收益的概率p1和损失的概率p-1为
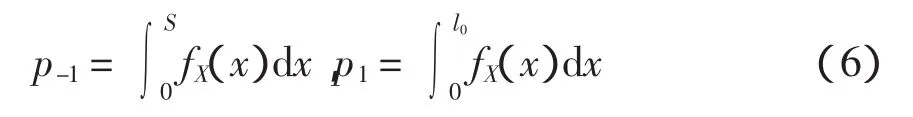
根据美国交通部统计数据,电动汽车日行驶里程服从对数正态分布[3]。其行驶里程概率密度函数fX(x)满足
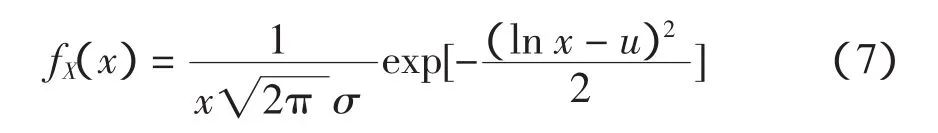
式中:u=3.2;σ =0.88。
设电动汽车在某决策方案下的收益为x1元,损失为x-1元,某初始荷电状态下的前景为f,根据前景值函数公式可求得其前景值V(f)为
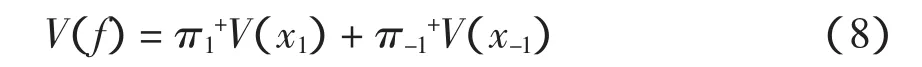
式中:π1+=w+(p1);π-1-=w-(p-1)。
1.6 临界决策点的求解
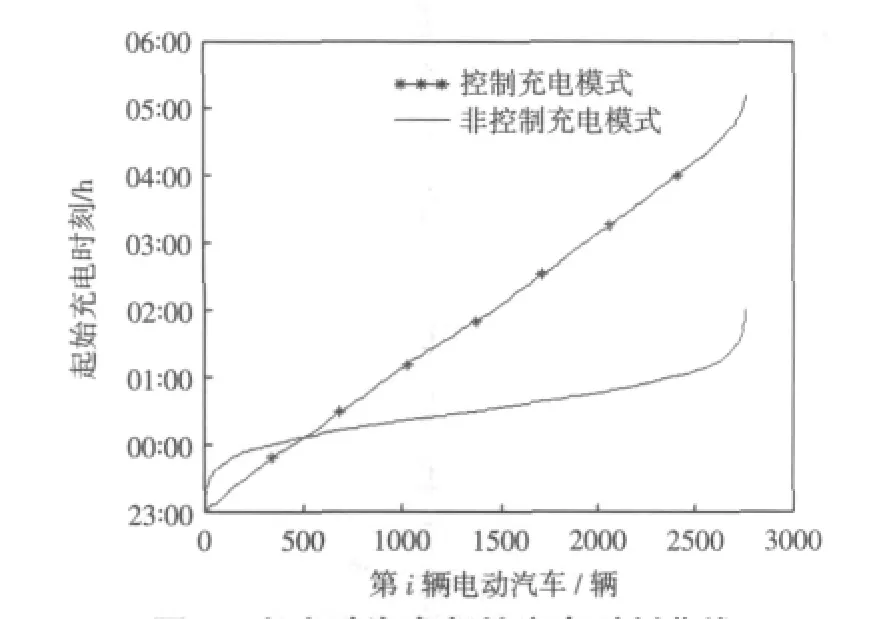
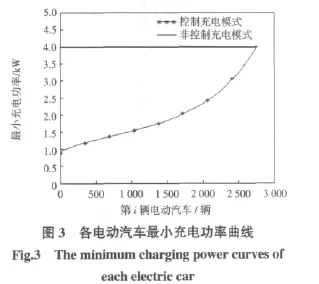
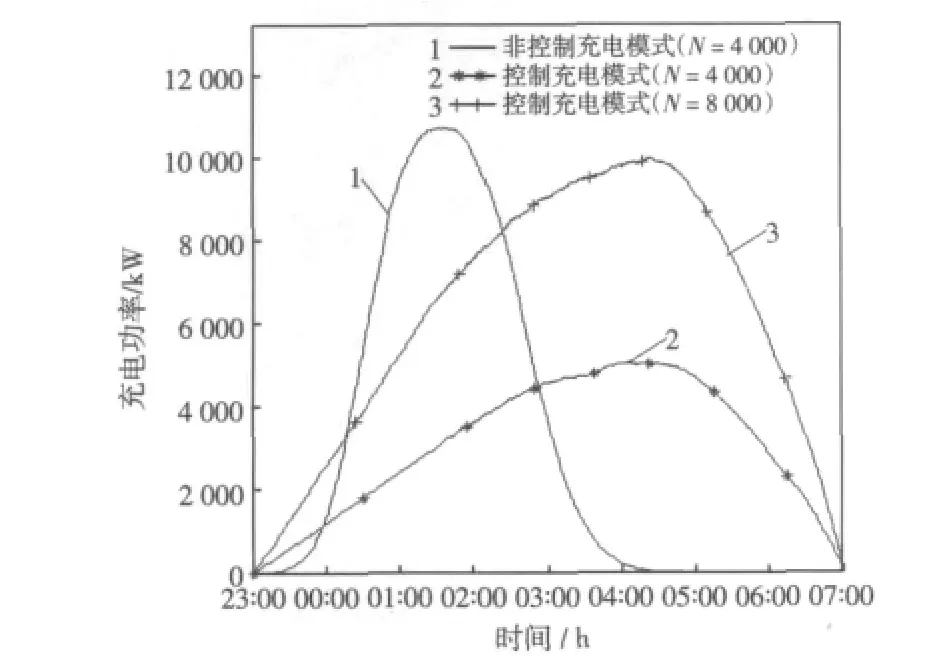
电动汽车是否充电的抉择分析。设任意初始荷电状态SOC0对应的剩余可行驶里程为l0km,求解任意剩余可行驶里程l0下电动汽车不选择充电的前景值;选择前景值为0的方案下对应的电动汽车的初始荷电状态SOC0为临界决策点SOCP。则当SOC0>SOCP时,由于在此种情况下电动汽车选择不充电时的前景值大于0,即当选择不充电时电动汽车相对参考点可能获得收益,所以电动汽车选择不充电;反之,当SOC0 设电动汽车的续航里程为Lmaxkm,临界决策点对应的电动汽车剩余可行驶里程为l0,假设剩余可行驶里程与荷电状态成简单的线性关系,则临界决策点SOCP为 由于大多数电动汽车主要集中在白天使用,晚上大部分时间处于闲置状态,因而在阶梯电价政策的诱导下,电动汽车的充电行为将主要发生在电价低谷时段。而在低谷时段,电动汽车在不同的充电模式下,其充电功率有很大的不同,其具体分析如下所述。 在不受控制的充电方式下,根据电动汽车慢速充电的时间要求,用户在低谷时段内自由选择开始充电时间,那么其开始充电的时刻将集中在低谷时段开始的一段时间内。由于其充电功率不受控制,所有电动汽车将以额定功率进行充电。由于其开始充电时刻具有较明显的随机分布特性,因而常采用蒙特卡洛序列法[9-10]对电动汽车充电行为进行模拟,进而得出各时刻电动汽车充电功率曲线,正如文献[4]中所述。 电动汽车负荷比较分散,且大多是居民负荷,因而希望电动汽车的充电功率尽量的低,使其更适用于家庭使用;又电动汽车负荷的接入可能对电网造成新的冲击,因而期望电动汽车的充电功率曲线比较平稳,使其不会对电网带来新的太大冲击;在此基础上,提出控制充电模式。在控制充电模式下,电动汽车可根据需求充电时间在允许的范围内自主选择充电起始时刻;并根据需求充电电量和充电起始时刻在允许的范围内选择适当的充电功率,以满足电动汽车充电功率的尖峰负荷尽可能小,功率曲线尽可能平稳的要求。其功率建模如下所述。 电动汽车充电抉择的模拟。对单辆需求充电的电动汽车(i=1,2,…,n)的起始荷电状态,抽取随机数进行模拟,即SOC0,i=yi。设临界决策点为SOCP,根据充电决策分析,当 SOC0,i 设电动汽车i的需求充电电量为Qi,则 设电动汽车最大充电功率P0充电,则电动汽车i慢速充电的需求充电时间Ti(SOC0,i)为 根据需求充电时间Ti(SOC0,i),设低谷充电时段为[ta,tb],则电动汽车 i最晚充电起始时刻tzi(SOC0,i)为 根据需求充电时间Ti(SOC0,i)和最晚充电起始时刻tzi(SOC0,i),则电动汽车充电起始时刻ti(SOC0,i)为 其中,xi为0~1之间的随机数。 设电动汽车实际充电时长为tsih,电价低谷时段长度为Tdh,由于需求充电电量为QikW·h,则电动汽车i实际充电功率pi为 其中,ti(SOC0,i)≤tsi≤Td-(ti(SOC0,i)-ta); 根据 tsi取值范围,则 pi满足 pi,a≤pi≤pi,b,且满足: 设电动汽车i在某种充电方案j下的充电功率为pj,i(j=1,2,…,n),在此充电方案下的需求充电时间为tj,i,设充电时段内任意时刻t时电动汽车在充电方案j下的充电功率为pj(t),则 其中,N为实际参与充电的电动汽车。 控制充电模式下,电动汽车充电功率约束条件。单辆车充电功率上、下限约束,即单辆车充电功率pi即不超过慢速充电的最大充电功率p0,又要不小于最小需求充电功率pi,a。单辆车的实际充电时间约束,即单辆车的实际充电时间ti应不小于需求充电时间Ti(x)而不大于最大可充电时间。则在控制充电模式下,电动汽车充电的约束条件为 控制充电模式下,电动汽车充电功率的目标函数。其一,为减小电动汽车充电负荷对电网的冲击影响,以各充电方案下任意时刻最大充电功率最小为目标。其二,为满足功率曲线更加平稳的要求,以各充电方案下各时刻的充电功率与平均充电功率的偏差之和最小为求解目标。 设某充电方案j下低谷时段内的最大充电功率为Pjmax,则目标函数f1为 设某充电方案j下某时刻的充电功率为pj(t),平均功率,则目标函数f2为 式(16)和式(17)进行归一化处理,构建控制充电模式下电动汽车的目标函数f为 根据约束条件和目标函数,运用遗传算法[11]求解满足目标函数的最优解,使用MATLAB求解电动汽车充电功率曲线,其求解流程如图1所示。其商业实现方式:电动汽车充电终端将其接入电网充电时间、电池需求充电电量等信息提交协调充电管理中心,管理中心调用协调充电优化程序计算各电动汽车的充电起始时间和充电功率,并将此信息下传到用户终端,电动汽车执行调度中心指令进行充电。 图1 控制充电模式下功率曲线求解流程Fig.1 Flow chart of power curve solution in controlled charging mode 相关参数设置:电动汽车电池容量Q0=20kW·h,额定充电功率P0=5 kW电池循环使用次数n1=1 000次,续航里程Lmax=100 km,需求充电时间T0=5 h,单体电池售价GB=15 000元;低谷时段充电电价GS=0.6元/kW·h;在外快速充电电价为Cq=1元/kW·h;电动汽车低谷时段充电前的荷电状态分布为 SOC0~N(0.6,0.12)[4];电动汽车日行驶最大里程S=320km;需求充电的电动汽车的数量N=4 000;低谷时段为 23:00—07:00,时长 Td=8 h。 电动汽车是否充电可能带来的费用,由式(1)和(2)可求得Ff=12,Fe=10。当电动汽车选择不充电时,由公式(3)可求得可能造成的收益和损失分别为 x1=12,x-1=-10.由式(4)可求得收益和损失的价值分别为V(x1)=8.9059,V(x-1)=8.905。设任意初始荷电状态SOC0下,对应的可行驶里程为l0km,在MATLAB环境下,运用公式(5)计算各可行驶里程l0对应的前景值,计算所得部分数据如表1所示。 表1 前景值计算结果Tab.1 Computation results of prospect value 分析表1的数据可得,当剩余电量可供电动汽车行驶56km时,V(f)的正值取得最小,为0.007 8。选择此时剩余电量的值为电动汽车充电的临界决策点。当剩余电量高于此值时,电动汽车选择不充电;当剩余电量低于此值时,选择充电。 电池花销费用对电动汽车充电行为决策的影响。当电池花销费用降低而额外充电费用不变时,比如当Ff=10,Fe=10,同理可计算各可能行驶里程下的前景值,计算结果如表2所示。分析数据可得,当剩余可行驶里程l0=65 km时,前景值V(f)的正值取得最小,为0.027 9。分析表1与表2数据可以看出,随着电池费用降低,临界决策点对应的剩余电量的可行驶里程在增大(65>56)。即随着电池费用降低,选择在家充电的电动汽车的数目将增加。 表2 前景值计算结果Tab.2 Computation results of prospect value 在外充电的电价对电动汽车充电行为决策的影响。当额外充电费用降低时,比如当Ff=10,Fe=8。同理可得,当剩余可行驶里程l0=55 km时,V(f)的值取得正最小,为0.063 4,如表3所示。分析表2与表3的数据可以看出,降低在外充电的费用时,临界决策点对应的剩余电量的可行驶里程在减小(55<65)。即随着额外充电费用降低,选择在家充电的电动汽车的数目将减少。 表3 前景值计算结果Tab.3 Computation results of prospect value 综上所述,电动汽车电池成本的花销及在外充电的充电电价都将影响电动汽车低谷时段是否选择充电的决策。当电动汽车电池费用降低时,选择在家充电的电动汽车的数目将减小;当在外充电费用升高时,选择在家充电的电动汽车的数目将增加。 临界决策点的求解。由上述分析可知,当Ff=10,Fe=10,临界决策点SOCP对应的剩余电量的可行驶里程l0=65 km。由公式(9)可求解出临界决策点的荷电状态为SOCP=0.65。即初始荷电状态值大于0.65的电动汽车都选择不充电,反之,选择充电。 不同充电模式下,电动汽车的充电功率的求解。考虑电动汽车充电抉择的影响,当Ff=10,Fe=10时,l0=65 km,SOCP=0.65。在不同充电模式下,使用MATLAB仿真可得不同充电模式下电动汽车的起始充电时刻曲线、最小充电功率曲线和所有电动汽车充电功率分布曲线。 不同充电模式下,计算需求充电的各电动汽车的起始充电时刻,其结果如图2所示。分析图2可知,在不受控制充电模式下,电动汽车起始充电时刻主要集中在前3 h内;而控制充电模式下,起始充电时刻比较均匀地分布在前6 h内。其说明在控制充电模式下电动汽车起始充电时间的选择更广泛。 不同充电模式下,求解满足充电要求的各电动汽车的最小充电功率,其结果如图3所示。分析图3可得,在非控制充电方式下,各电动汽车恒定功率充电;而在控制充电方式,电动汽车的充电功率比较灵活,其充电功率可在范围内根据需求充电电量适当选择充电功率。 图2 各电动汽车起始充电时刻曲线Fig.2 Start charging time sequence curves of each electric vehicle 不同充电模式下,所有需求充电的电动汽车的充电功率曲线如图4所示。分析图4曲线1和曲线2可得,在不受控制充电方式下,电动汽车的需求充电功率曲线出现比较大的尖峰,且分布不均,电动汽车主要集中在一段时间[0:00,4:00]内充电;而在受控制充电模式下,电动汽车的需求充电功率曲线在整个低谷时段内比较平稳,电动汽车充电分布比较均匀。由于非控制充电模式下,电动汽车的充电功率出现较大的尖峰,最大值为11 084 kW(如图4中曲线1所示),因而将给电网带来新的冲击;而在受控充电模式下,充电功率比较平稳,其最大值为5 159 kW(如图4中曲线2所示),因而,在同等情况下,控制充电模式下电网将能承担更多的电动汽车充电。以额定电源功率10 000 kW为例,在不受控制充电模式下难以承受4 000辆电动汽车充电,即图4中曲线1的峰值超过了10 000 kW,而在受控制充电模式下,8 000辆电动汽车充电是可行的,因其最大功率9 956 kW(如图4中曲线3所示)低于10 000 kW。 图4 电动汽车充电功率曲线Fig.4 Power curves of electric vehicle (1)本文基于前景理论的方法分析了电动汽车的充电抉择行为,求解出充电抉择临界决策点,证明了该方法的可行性。 (2)分析了电动汽车电池固定成本费用和在外充电电价价格变化对充电行为决策的影响;并得出结论,当电池费用越高时,选择低谷时段充电的电动汽车的数目将越多;当在外充电电价价格降低时,选择低谷时段充电的电动汽车数目将减小。 (3)分析了受控制充电模式下和不受控制充电模式下电动汽车的充电功率,求解出各自充电功率曲线;分析比较得出结论,在受控充电模式下,电动汽车的充电负荷更加平稳,未出现新的尖峰,因而在同等情况下现存电网将能承受更多的电动汽车充电。 [1]宋永华,阳岳希,胡泽春(SongYonghua,YangYuexi,Hu Zechun).电动汽车电池的现状及发展趋势(Present status and development trend of batteries for electric vehicles)[J].电网技术(Power System Technology),2011,35(4):1-7. [2]王晓寅,刘俊勇,唐勇,等(Wang Xiaoyin,Liu Junyong,Tang Yong,et al).基于logit模型的电动汽车充放电研究(Study on EV charging and discharging based on logit model)[J].华 东 电 力 (East China Electric Power),2011,39(2):198-202. [3]田立亭,史双龙,贾卓(Tian Liting,Shi Shuanglong,Jia Zhuo).电动汽车充电功率需求的统计学建模方法(A statistical model for charging power demand of electric ve-hicles)[J].电网技术(Power System Technology),2010,34(11):126-130. [4]罗卓伟,胡泽春,宋永华,等(Luo Zhuowei,Hu Zechun,Song Yonghua,et al).电动汽车充电负荷计算方法(Study on plug-in electric vehicles charging load calculating)[J].电力系统自动化(Automation of Electric Power Systems),2011,35(14):36-42. [5]Bashash Saeid,Moura Scott J,Fathy Hosam K.Charge trajectory optimization of plug-in hybrid electric vehicles for energy cost reduction and battery health enhancement[C]//American Control Conference.Baltimore,USA:2010. [6]Clement K,Haesen E,Driesen J.Coordinated charging of multiple plug-in hybrid electric vehicles in residential distribution grids[C]//IEEE/PES Power Systems Conference and Exposition.Seattle,USA:2009. [7]Qian Kejun,Zhou Chengke,Allan Malcolm,et al.Modeling of load demand due to EV battery charging in distribution systems[J].IEEE Trans on Power Systems,2011,26(2):802-810. [8]赵凛,张星臣(Zhao Bing,Zhang Xingchen).基于“前景理论”的路径选择行为建模及实例分析(A traveler route choice model based on prospect theory and case study)[J].土木工程学报(China Civil Engineering Journal),2007,40(7):82-86. [9]姚李孝,赵 兵,伍 利,等(Yao Lixiao,Zhao Bing,Wu Li,et al).基于混合算法的复杂配电系统可靠性评估(Hybrid method for the reliability evaluation of complex power distribution system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(6):96-102. [10]夏成军,王 强,邹正华,等(Xia Chengjun,Wang Qiang,Zou Zhenghua,et al).电压骤降概率评估的建模与仿真(Modeling and simulation for probabilistic assessment of voltage sag)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(1):86-90. [11]雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2004.
2 电动汽车充电模式分析
2.1 不受控制充电模式下电动汽车的需求充电功率
2.2 控制充电模式下电动汽车的需求充电功率

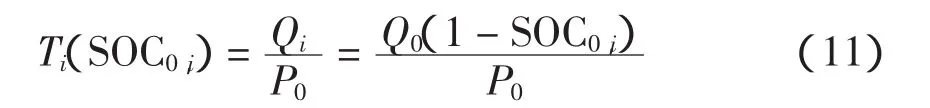

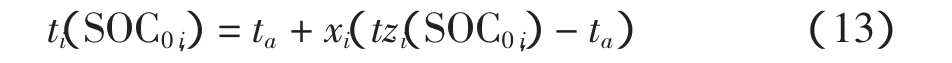

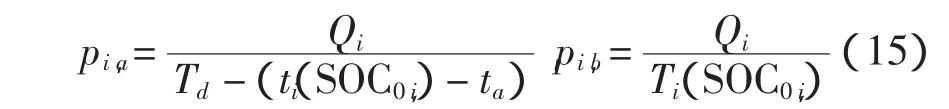

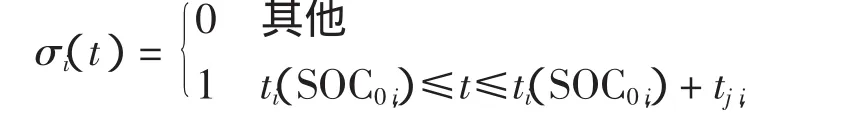
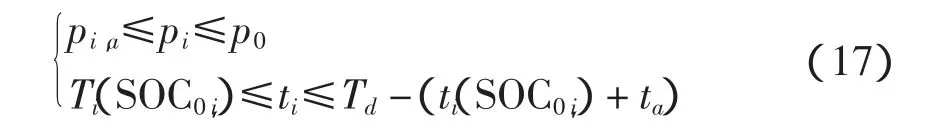

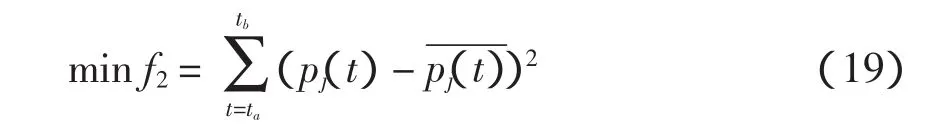
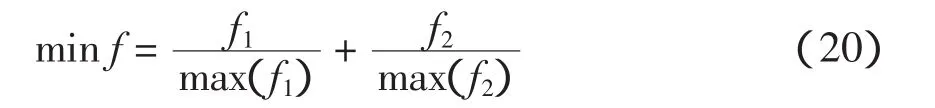
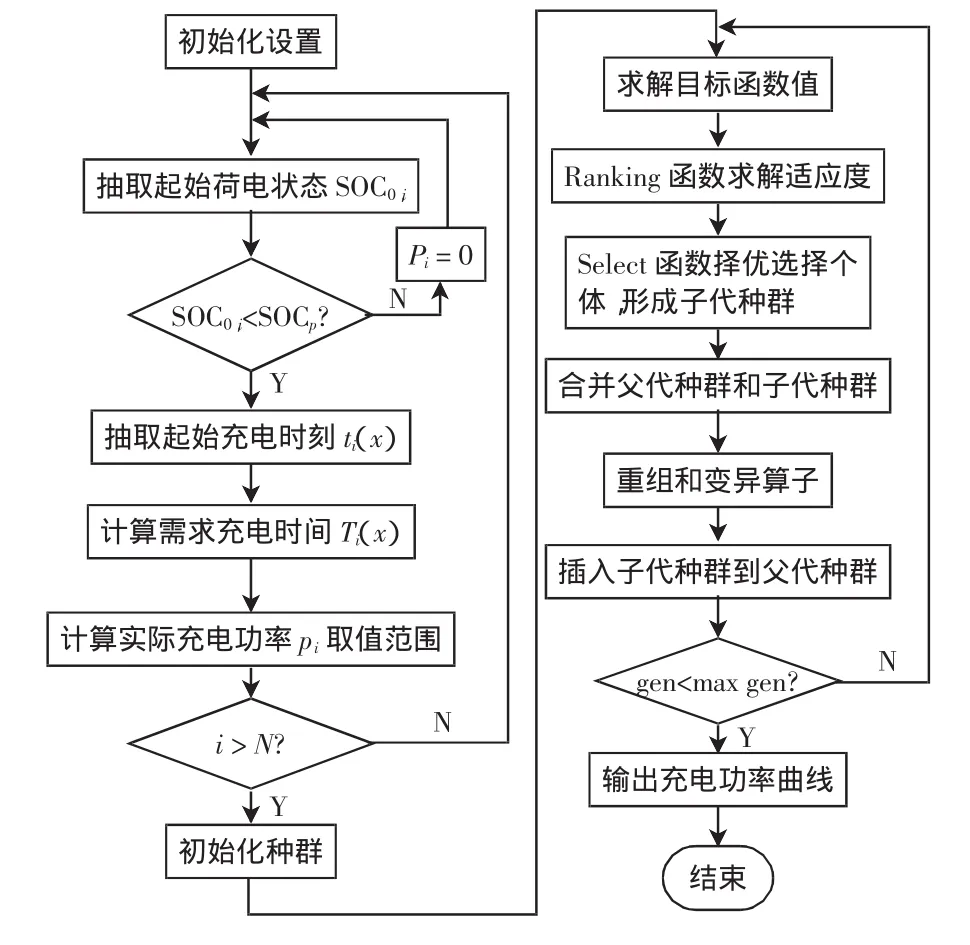
3 算例分析
3.1 电动汽车充电决策分析
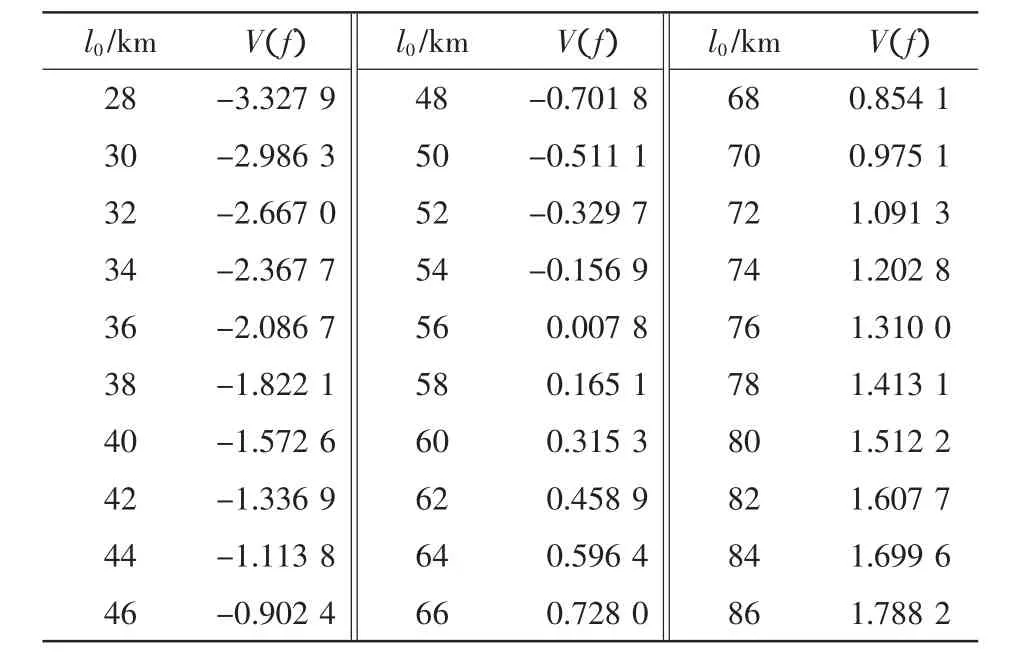
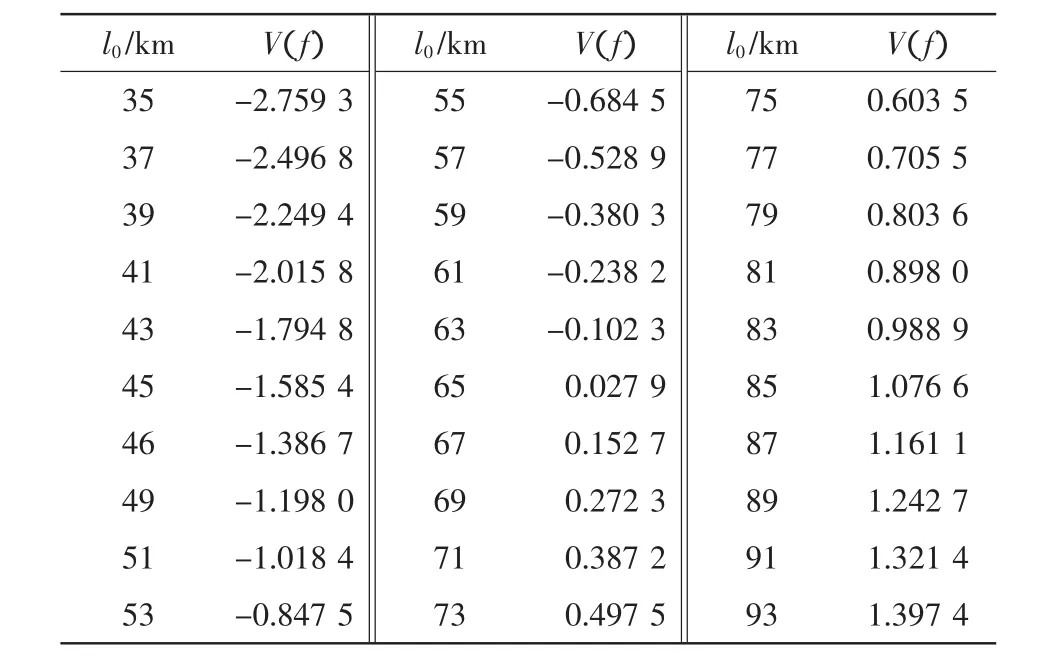
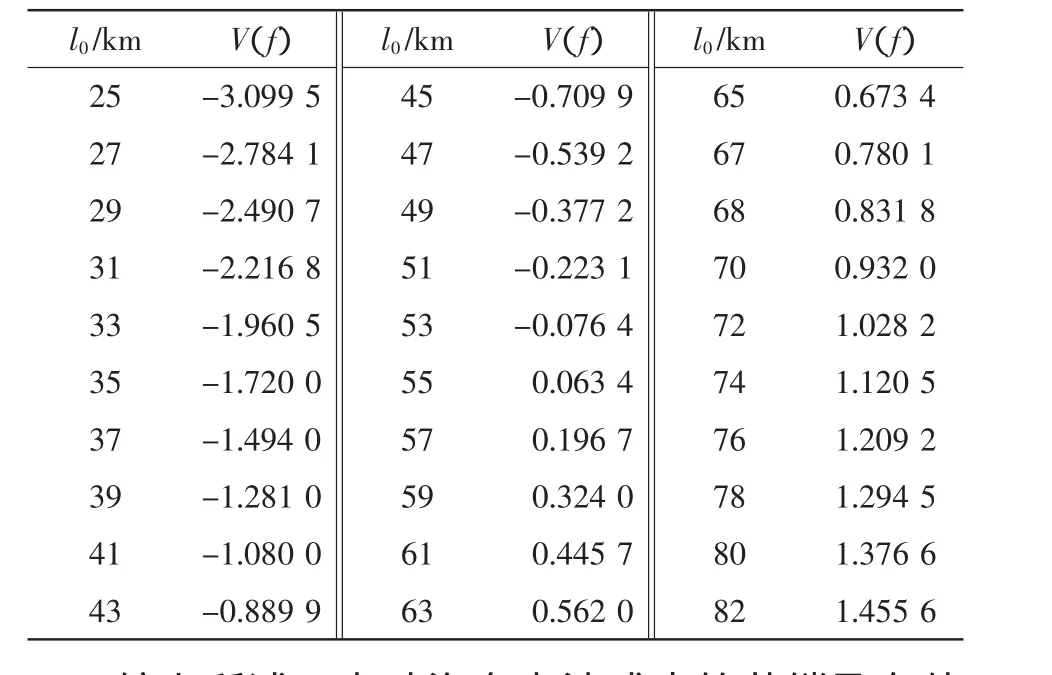
3.2 不同充电模式下电动汽车的充电功率分析
4 结论
