基于ANSYS Workbench对立式车床横梁的模态分析*

孙广敏，安丰柱

(1.滕州市产品质量监督检验所，山东 滕州 277500;2.山东省质量技术监督干部学校，山东 济南 250000)

1 引言

立式车床适用于对大型盘类零件的加工，而单立柱立式车床适用于直径较小的盘类零件，其具有结构紧凑的优势，在机械制造行业中广泛应用。但由于单立柱立式车床在加工过程中并不是采用双立柱式立式车床所采用的简支梁结构，而采用的是悬臂梁，这就造成了在加工过程中由于震动等现象的形变更加严重。因此，横梁的结构是否合理对机床的加工精度、工作稳定性、加工效率、使用寿命等衡量机床的各个性能指标都有很大程度上的影响［1］。

横梁的结构主要为箱体结构，这样的结构对于横梁来说可以有效降低切削力对于加工时的影响，对于横梁的振动也有一定的克制作用。在机床运行中，横梁的振动主要由传动系统的精度误差，切削过程中工件的不均匀性等造成的机床受迫振动与机床部件在工作过程中发生的弯曲或扭摆、运动部件在低速运动时产生爬行现象等造成机床的自激振动［2］。这些振动的频率与机床的横梁固有频率相等或接近时，会造成共振现象生成。严重影响机床的加工精度与表面质量，更重要的是造成机床零部件的破坏，降低使用寿命。因此有必要对机床的横梁进行模态分析。笔者利用有限元软件ANSYS Workbench对横梁进行模态分析，并对其前6阶固有频率与与之相对应的振型进行分析［3］与研究，为日后的结构优化设计提供合理的理论支持。

2 振动数学模型

在对数控立式车床的立柱动力学分析中，物体的模态参数由固有频率与与之相对应振型组成。这两个参数主要由物体的结构、质量和硬度决定。因此，可根据自由振动基本微分方程［4］对其分析。

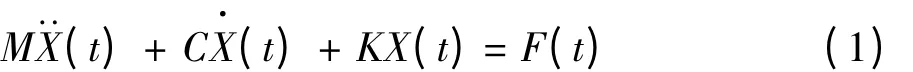
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;X为位移向量;F(t)为作用力向量;t为时间。

由于此结构阻尼较小，对固有频率与振型影响较小，故可忽略不计。因此当F(t)=0时，方程变为:

结构自由振动时，结构上的各个节点做简谐振动。各点的位移为:

式中:A为自由振动时各节点的振幅向量。

将式(3)、(4)代入式(2)中得:

式中:式(5)是关于广义特征值ω2的n次方程，ω对应于每一阶固有频率。

3 建立三维模型

本研究分析的模型为单立柱立式车床横梁结构。在进行有限元分析之前需要依据实际要求建立三维模型。笔者利用Solidworks建立了合适的分析模型。在建模过程中，为方便计算，同时又要尽量保证计算结果的准确性，对模型进行了合理的优化，如对于结构影响不大的螺纹孔结构做省略处理。如图1所示为横梁的三维模型图。其材料属性如表1所示。

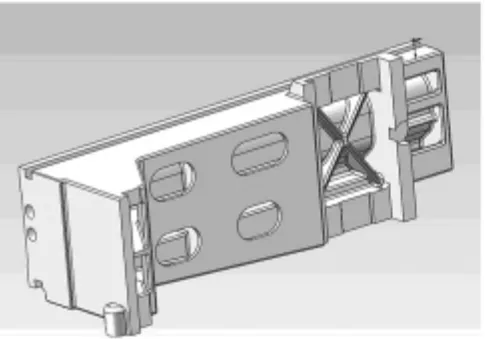
图1 横梁三维模型

表1 材料属性

4 网格划分

在划分网格时选用尺寸控制法，网格类型选用四面体，此种单元具有结果较为精确，在弯曲载荷下不容易变形等优势［5］。单元大小选用类型为近似全局尺寸100 mm。其划分网格后的模型如图2所示。

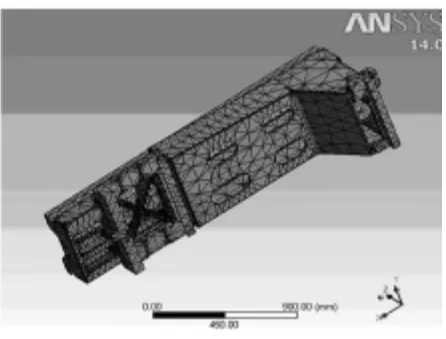
图2 网格划分

5 模拟仿真

在利用ANSYSWorkbench对横梁进行模态分析时，需要对条件进行设定。具体设定为:

约束条件:根据实际的机床安装与使用条件，对横梁与立柱上的轨道做完全固定约束。

ANSYSWorkbench在对物体进行模态分析时，选用Lanczos方法［6］，Lanczos方法既能够在处理大型刚体振动求解时最为有效。

阶次选择:研究发现，具有1000个自由度以上的振动系统，提取其前三阶振型，其精确度就可达到90%以上，若对前10阶振型进行提取，其精确程度可达到99%以上［7］。因此为了方便计算，对某些高阶次的振型可以忽略不计，主要对其低阶振型进行分析。在计算过程中，提取前6阶振型进行分析。

6 模态仿真结果

利用ANSYSWorkbench对机床横梁进行划分网格，在分析步中的场输出进行设置位移大小，而后对其进行有限元计算、求解。在可视化模块里得出零件的前6阶模态分析参数，结果如表2所示。振型图如图3～8所示。

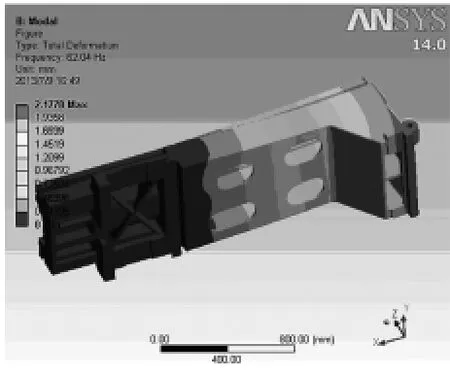
图3 第1阶模态分析图

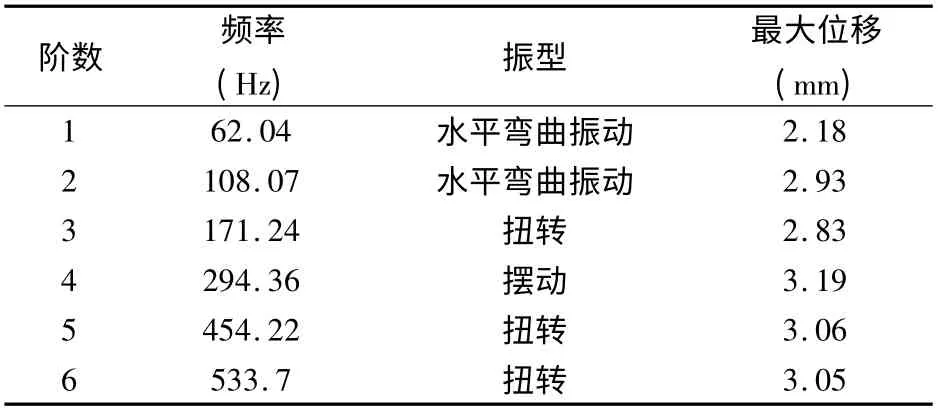
表2 横梁模态分析结果

通过分析结果看出，除第3阶振型以外，由振动造成最大位移多发生在横梁右端的凸起位置处，其振动造成的最大偏移都在1 mm以上。第3阶振型最大位移区为安装刀架的轨道最右边。当振动频率达到294.36 Hz时，此时横梁形变最大，最大值达到3.19 mm。此时发生横梁的前后摆动现象。而在其他的频率下，横梁的振动造成的变形都超过2 mm。

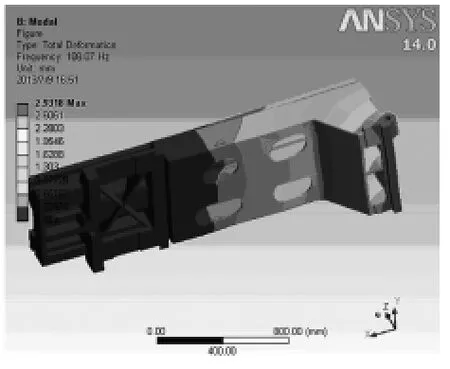
图4 第2阶模态分析图

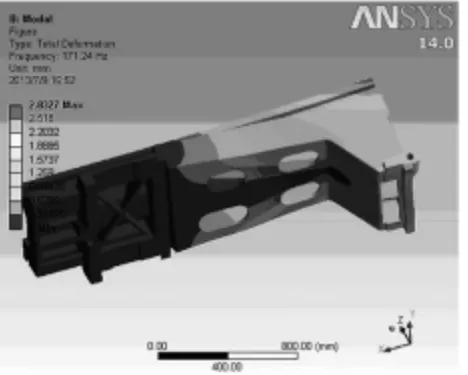
图5 第3阶模态分析图

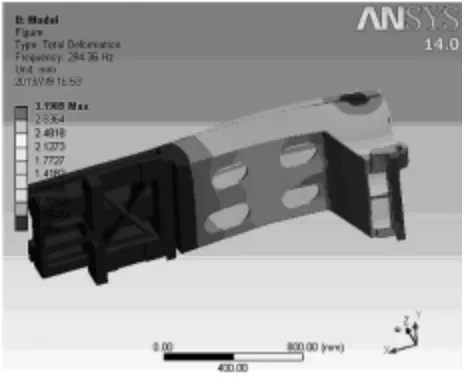
图6 第4阶模态分析图

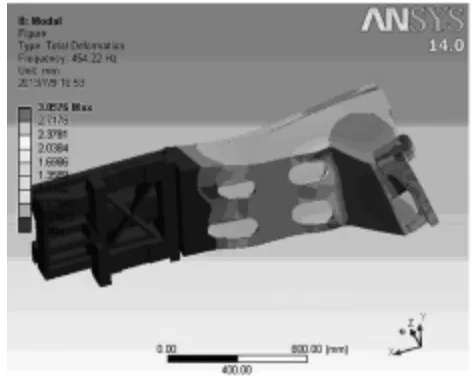
图7 第5阶模态分析图

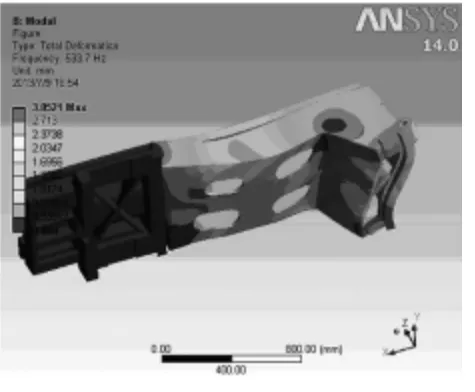
图8 第6阶模态分析图

从前6阶模态振型中可清楚的看到，每阶振动都会造成横梁上的与刀架连接轨道的变形，此时会影响到加工精度。而最右端则是变形最大的区域，此处在长期由共振作用引起的交变载荷作用下，容易造成疲扰损坏，因此有必要注意在日后的优化结构中改进其结构。

7 结语

根据以上的分析可看出，该立柱在设计中结构较为合理，其第1阶振型发生在62.4 Hz时刻，此时频率高于对操作人员身心损害最大的次声波(f≤20 Hz)。但是也应当注意的是前6阶振型发生最大的振动区域都是发生在最右边，这说明其结构并不是非常理想，在工作时容易造成疲扰破坏，应在日后的结构改进时注意增加其局部的刚度与阻尼［8］。同时，在生产作业过程中应尽量避开与其固有频率接近的振动干扰，防止产生共振。

［1］ 诸乃雄.机床动态设计原理与应用［M］.上海:同济大学出版社，1987.

［2］ 韩益建.数控机床的振动故障分析［J］.制造技术与机床，2009(5):134-135.

［3］ 田育耕，石 晶，段 敏，等.柴油机气缸盖的模态分析［J］.机械设计与制造，2005(11):34-35.

［4］ 刘延柱，陈文良，陈立群.振动力学［M］.北京:高等教育出版社，1998.

［5］ 王玲娟，张 丽.基于ABAQUS的桥式起重机箱型主梁模态分析［J］.煤矿机械，2011(7):86-88.

［6］ 李杰红.求解大型对称线性方程组的循环收缩Lanczos算法［J］.天津科技大学学报2011(2):75-78.

［7］ 满 佳，徐燕申，张学玲.超精研机床的振动抑制技术研究［J］.组合机床与自动化加工技术，2006(6):45-49.

［8］ 夏国林，张代胜.轿车白车身模态分析与振型相关性研究［J］.计算机应用，2008(1):12-16.