垂直轴风力机翼型动态气动性能研究*

2013-06-28聂佳斌祖红亚

机械研究与应用 2013年3期

聂佳斌，李春，祖红亚

(上海理工大学能源与动力工程学院，上海 200335)

1 引言

垂直轴风力机具有叶片疲劳载荷小，结构重心低稳定性能好，制造及安装简单等优势［1］;但也存在着启动性能差，难以有效摆脱动态时速效应影响等劣势。通常垂直轴风力机采用对称翼型作为其叶片的基础造型。但由于垂直轴风力机运行时复杂的气动特性，笔者提出了应用于垂直轴风力机的两段式翼型，参考NACA0012翼型，结合气动以及结构性能，初步建立了两段式翼型的主要几何参数。以CFD数值计算为实验平台，给出了两段式翼型应用于垂直轴风力机的动态气动性能。

2 模型及计算

2.1 垂直轴风力机运行机理

升力型垂直轴风力机叶片方位角变化从0°～360°，因此通常叶片采用对称翼型，如NACA0012，NACA0012及NACA0018等。图1给出了风力机做功原理。图1中V∞为来流风速;Vt为切向线速度;Vw为合速度;α为攻角;Fl为升力;ψ为方位角;Fd为阻力;ω为角速度;λ为尖速比;R为风轮半径。

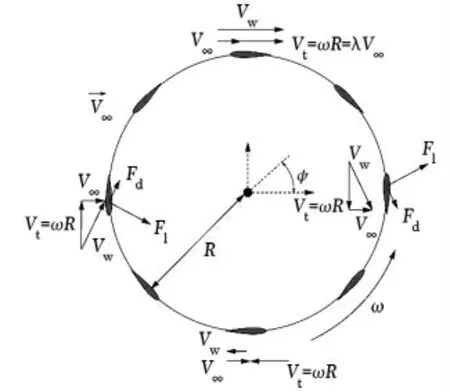
图1 垂直轴风力机做功原理

在说明运行原理之前，首先定义尖速比概念，表达式如下:

对于垂直轴风力机，叶片所受相对速度是切向线速度与来流风速的矢量合。因此，翼型的攻角范围并非-360°＜α＜360°，实际上，叶片攻角变化是关于叶片尖速比以及叶片方位角的函数，如式(2)所示:

随着叶片尖速比的增加，叶片攻角范围也更趋于平坦，如图2所示。这是由于当尖速比越大时，叶片所受相对来流风速中，切向线速度所占比重上升导致的。本文CFD计算中的中尖速比为4。

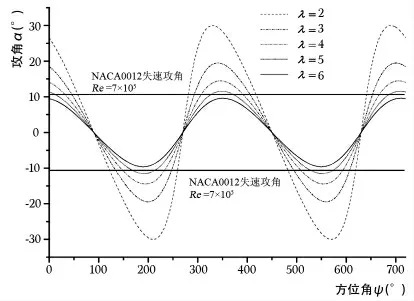
图2 不同尖速比攻角与方位角对应关系

垂直轴风力机叶片在其旋转周期内，升力都提供正向转矩，其做功值大于阻力产生的负转矩，这便是升力型垂直轴风力机运行机理［2］。

2.2 两段式翼型构造

构造副翼的目的在于改善风力机气动性能，尤其是在近失速攻角范围内，通过副翼转向，改变翼型上下表面压力，优化气动性能。副翼对垂直轴风力机叶片气动影响明显，浙江大学徐暲［3-4］等人研究发现，合适的翼型尾缘结构可提高翼型气动性能，提高风力机的输出功率。

翼型主体采用经典NACA0012翼型截面，即图3示意叶片中的前半部分，而副翼可以绕其旋转中心在±30°范围内摆动。其旋转中心位于翼型弦长1/4处。

图3 两段式翼型截面示意

两段式翼型最大优势在于改善翼型气动性能，如风力机启动时，由于转速较慢导致升力较弱，改变副翼摆角能够改变风力机上下表面的压差从而使风力机尽快进入额定转速范围。同样，在两段式翼型副翼摆角的作用下风力机叶片失速，从而避免在极端风载情况下的刹车损伤。如此对降低风力机疲劳载荷具有重要意义。

2.3 计算域及网格划分

CFD计算主要采用滑移网格技术描述旋转几何体。将计算区域划分为3个域，它们分别为内流域、主体旋转流域以及外流域，3个流域之间设置交界面，如图4所示，网格总数532 14，翼型周围网格划分如图5所示。

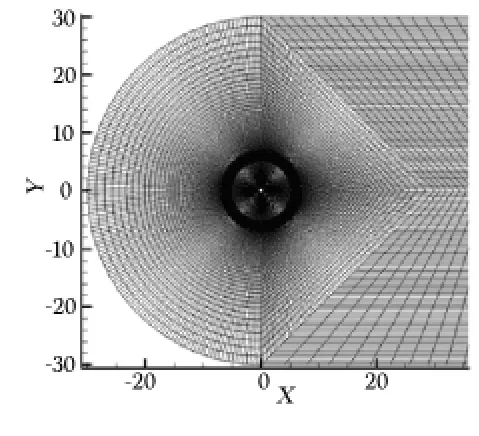
图4 流场整体网格划分

图5 翼型周围网格划分

流体介质选用空气，密度ρ=1.225 kg/m3;动力粘度μ=1.789 4×10-5kg/(m·s);来流速度V为10 m/s;计算雷诺数Re=6.85×105，马赫数Ma=0.03。整体上下边界设置为前端速度进口(Velocity inlet)，后端边界设置为压力出口(Pressure outlet)。

2.4 控制方程

基本雷诺平局Navier-Stokes控制方程如下:连续方程:

动量方程:

能量方程:

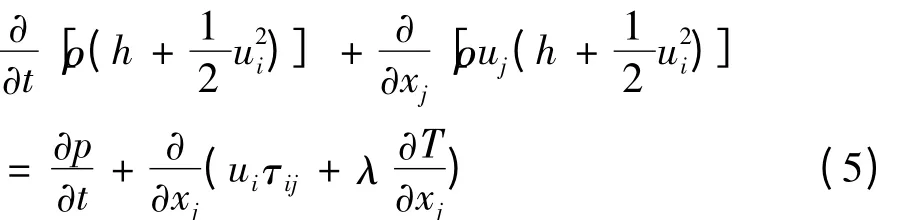
式中:τij为应力张量，h为总焓，由以下方程确定。

理想气体状态方程:

对于特定垂直轴风力机，因旋转速度相对于风速较低，风力机叶轮周围流动可认为是由不可压缩NS方程控制［5］。可使用放在叶片上的旋转坐标表示，方程是如下所示。

式中:X，Y，U，V分别是旋转坐标系中的方位和速度。

它们与静止坐标系的关系如下:

式中:x，y为方位;u，v为速度在静止坐标系;θ为旋转角度。

3 结果分析

动态失速最为明显的特征表现为涡脱落过程，即动态失速可通过涡脱落及其对翼型低压面的扰动效应加以描述。对于俯仰运动的翼型而言，其上仰运动时产生的Cl和CD值，远高于对应攻角的静态值。此现象由翼型非定常运动和边界层分离共同引起。

图6直观的给出了风力机旋转之初，尾迹涡形成及发展全过程。最终CFD计算4.75个周期后的尾涡分布如图7所示。由于三叶片风力机相互叶片夹角120°，因此只需给出1/3的运行周期便能表征这个周期下运动情况。由于纸质文本的限制，论文无法给出整个动态过程中流场的变化，只能以方位角30°为一个间隔予以表示。

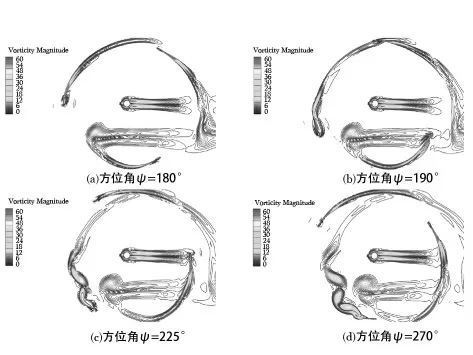
图6 尾迹涡发展过程

图7 流场涡量分布

从整个流场的涡量图可清晰的观察到每个周期的失速涡发展、脱落及耗散的过程，同时为更好的说明动态失速涡的特点，根据图2将翼型与相对来流间的运动方式分为上仰和下俯两个阶段，其中不同的尖速比划分的角度不同，当λ=4时，下俯阶段对应的方位角为-14.5°＜ψ≤194.5°，上仰阶段的方位角为194.5°＜ψ≤346.5°。

为深入了解垂直轴风力机翼型周围动态流场的特点，将局部放大不同方位角下翼型周围的速度、流线以及涡量分布，其中图8给出了翼型不同方位角的涡量分布，其中，图8(b)中翼型方位角ψ=350°，此时攻角α=14.3°，大攻角状态下能观察到翼型尾缘处对旋的尾缘涡呈条状，同时其主体依旧附着于翼型表面，因此形成了图6中流场上半区域中的条状对旋涡。图8(a)中翼型方位角ψ=200°，攻角α=-14.4°，此时的对旋涡形状呈圆形，区别于下俯过程中的条状形态，同时动态失速涡脱落特征更为明显，也就形成了图7中流场下半区域中类似于卡门涡的涡系。

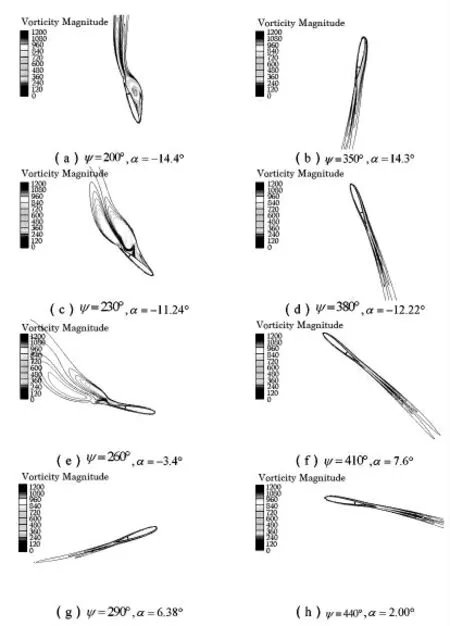
图8 翼型尾涡分布

攻角前的负号可理解为来流作用在翼型上下2个不同的表面，而翼型为对称，这样α=-14.4°在静态条件下意味着攻角大小为14.4°，但作用在翼型背面。从图8(a)、(b)的对比能够发现，同样是14.4°大小的攻角，却形成了不同尾涡结构。整体流域中，从涡系的整体形态上能区分出翼型上仰以及下俯的区域，上仰过程中脱落的涡主要呈条状，而下俯过程中脱落的涡系则呈圆形，而这些现象的主要原因是翼型的动态影响，由于翼型自身的运动趋势，导致其攻角始终变化，翼型对于来流始终表现为上下煽动的对应关系。

垂直轴风力机运行整个周期内动态尾迹涡的特点可归结为以下几点:

(1)在翼型快速下俯运动过程中，尽管边界层内部会发生逆流现象，但整体流动仍保持附着状态，并超出稳定分离点以外。

(2)当上仰运动的翼型处于大攻角工况下，翼型前缘开始出现动态失速涡并沿上表面迅速发展。

(3)动态失速涡逐步由翼型表面分离并脱落于尾流中。

(4)在翼型尾缘处产生对旋涡，并与主涡流相互作用。

(5)在翼型上仰运动过程中，产生强度较强的顺时针(翼型前缘处)或逆时针(翼型尾缘处)二次涡以及高阶次涡。

(6)随着翼型下俯运动的继续，流动开始表现为由前缘至尾缘的再附着过程。整个翼型振荡运动周期中，其下俯运动中流动再附着所对应的攻角，远小于上仰运动中流动分离所对应的攻角。

(7)通过翼型尾缘涡的不同形态可判断叶片是处于上仰过程还是处于下俯阶段。显然，翼型运动的动态效应及其产生的涡动力学现象会影响到作用在翼型上的整体气动力与力矩。

获取垂直轴风力机运行时的气动特性参数需要对CFD监视得到的数据进行一定的修正，这是由于风力机翼型始终处于运动状态导致数据处理上的难度增加。CFD计算时监视到的升阻力沿着水平和竖直两个方向分布，而翼型升阻力的定义中，升力的方向为垂直于来流方向向上，而阻力则沿着来流方向，因此得到的监视数据需要坐标变化。此时升阻力系数的方向需要考虑方位角及攻角变化的联合关系，攻角是方位角的函数因此升阻力系数的方向只与方位角一个量有关。

升力系数方向角:

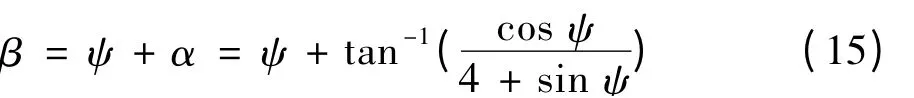
阴力系数方向角:

其中，CFD计算中，升力系数定义如下:

式中:Fl为升为;V为参考速度;A为作用面积;Clm为CFD监视升为数据。

由于实际运行过程中，翼型受到的相对来流速度的大小是变化的，且CFD计算时监视到的Clm是以V为恒定参数计算得到的，因此最终数据需要经过相对风速比的修正。具体转换如下:

式中:Clm为CFD升力监视值;Cdm阴力系数监视值。

动态情况下，翼型升阻力显示了迥然不同的特性。相比静态情况下升力系数随攻角变化成一条直线的趋势不同，翼型运动过程中的升力或阻力系数随攻角呈环状周期形变化，无论是上仰或是下俯过程，其升力或阻力系数值都将偏移静态值。图9给出了翼型动态情况下升阻力系数变化情况，图9(a)～(d)分别是第一、二、三以及第四周期下升力系数变化情况，从图中能够看到升力系数总趋势变化不大，但各曲线形状稍有不同，这是因为第一、二周期时风力机周围流场还未达到稳定，叶片尾流还未完全发展。等到了后几个周期就能发现明显的周期变化规律，这表征了风力机流场已趋于动态的周期变化规律。

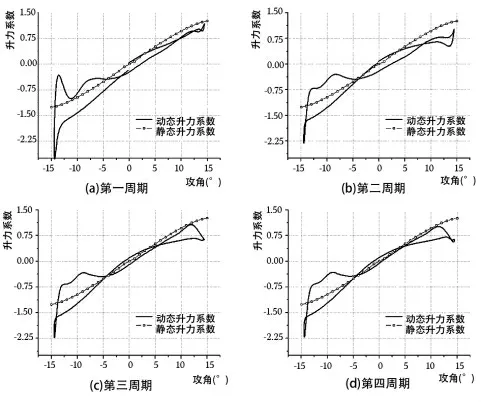
图9 翼型动态升力系数与攻角变化关系

图10给出了动态升力系数随方位角ψ的变化关系，由于方位角即翼型绕主轴公转时所处的位置，通过它能够直观的找到风力机翼型最大升力所处方位角。结合图8能够了解到虽然攻角大小相等，但上仰以及下俯是所能得到的最大升力系数却不同，显然当ψ⊂(90°，270°)时其升力系数比ψ⊂(0°，90°］∪［270°，360°)来的大，这表明翼型处于上风半周期时其受到的升力大。

图10给出风力机运行时翼型动态阻力系数，从图线的形态上能发现它虽然是环状分布，但总体结构较静态偏差不大，只有在下俯至大攻角时，其值会有突然的明显抬升，这是因为尾涡脱落造成的。随着周期的推移，阻力系数趋于动态的周期变化，动态流场结构虽然比较复杂，但其分布是有规律的。在90%的攻角范围内，阻力系数维持在0.05以下，这对于风力机的运行比较有利。同样，动态阻力系数环状的分布特性也是由于翼型对于攻角不断的俯仰运动导致的，虽然在中高尖速比下偏移特性不明显，但当尖速比减小时，偏移量将明显增加，尤其是当翼型大范围运行于失速攻角以外时，阻力整体平均抬升明显，这是导致升力型垂直轴风力机启动性能差的原因之一。

图10 翼型动态升力系数与方位角变化关系

图11给出了动态阻力系数随方位角的变化关系，从中发现翼型处于180°＜ψ＜240°时，阻力系数抬升明显，同比此方位角下的升力系数虽然出现了极大值，但由于阻力系数的增加，导致了此方位角下翼型的气动性能并不优越。同样，判定翼型系统性能的标准还应参考升阻比的大小，如图12所示。

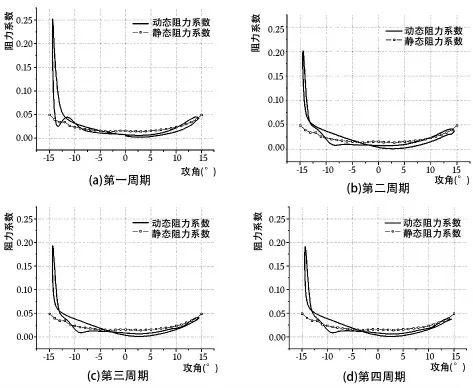
图11 翼型动态阻力系数随攻角变化关系

图12 翼型动态阻力系数随方位角变化关系

图13给出了升阻比随攻角的变化关系，而图14给出了升阻比随方位角的变化关系。能够发现升阻比的极大值出现在攻角α=4°左右，对应于方位角在ψ=70°附近，方位角从ψ=0°发展至ψ=90°时，虽然攻角一直在减小，但升阻比却是一个先增后减的趋势，在ψ=70°时迎来一个极大值后，迅速减小至0。同样，升阻比曲线同样印证了升力极大值时气动性能并非一定最优。

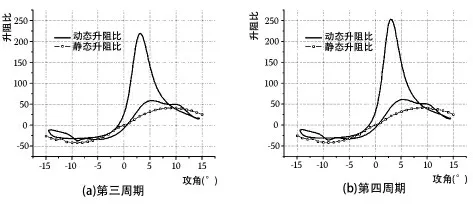
图13 翼型动态升阻比随攻角变化关系

图14 翼型动态升阻比随方位角变化关系

无论是升力或是阻力系数，其与静态值整体偏差不大，从本质上翼型气动参数与种类直接相关。但动态气动性能对于研究垂直轴风力机在流场中的效率是不可忽略的因素，比如其阻力瞬时脉动性的提升让风力机做功能力减弱等。结合翼型动态升阻比与翼型周围涡量分布情况(见图8)可发现，圆形尾涡区域伴随着明显的动态失速涡，其翼型升阻比明显较条形尾涡的翼型升阻比低。条形尾涡翼型周围虽然存在失速涡的脱落，但相对于来流与翼型表面结合的依旧非常紧密，似乎翼型没有发生失速分离。