3 MW风力机叶片设计建模与模态分析*

武玉龙，李 春，高 伟

(上海理工大学 能源与动力工程学院，上海 200093)

1 前言

近年来，风能已成为可再生能源中发展最快的清洁能源，同时也是最具大规模开发和商业化发展前景的可再生能源［1］。风力发电是风能利用的主要方式［2］。叶片是风力机的关键气动部件，其展向长、弦向短的特性，在表现出较好柔性的同时，又是一种容易发生振动的细长弹性体。因此，大型风力机叶片在复杂的外在激励作用下易产生振动，为避免叶片共振造成破坏，须对叶片进行模态分析，从而确定叶片结构的振动特性，即固有频率和振型［3］。

通过在叶片叶尖布置小翼，可改善叶片气动布局，当自然风吹该叶片时可增加叶片压力面与吸力面的压差，减少风力机叶尖端漩涡，减少叶尖损失，提高风力机的输出功率［4］。因此有必要对带有叶尖小翼的风力机叶片进行模态分析，从而确定小翼对叶片各阶振型的影响。

2 叶片设计建模

叶片设计是风力机设计的核心和重点，叶片的气动设计是叶片设计的关键，它对风力机的性能有重大影响。叶片设计包括计算风轮直径，确定叶片数，选取各叶素翼型，计算各叶素的弦长和桨距角。叶片设计的基本步骤为:①确定额定风速及风力机的额定功率;②计算风力机的风轮直径;③确定叶尖速比;④选定叶片翼型及叶片数目;⑤计算各叶素的弦长及扭角;⑥对叶片进行三维建模。

笔者所设计的叶片采用多翼型叶片。对叶片顶部翼型结构强度方面的要求不高，翼型一般较薄，但对气动方面的要求较高;因为叶片顶部是风能捕捉的主要部分，因此该部分翼型要求具有较高的最大升阻比、良好的失速特性和低粗糙度敏感性。

叶片顶部翼型特别是叶尖翼型对最大升力系数的要求并不是最高，NREL的研究表明，适当降低叶尖翼型的最大升力系数，可减小负荷，增加年平均能量输出。对叶片根部的翼型，则更侧重于结构强度的要求，翼型一般都较厚;气动特性上，除了要求有高的最大升力系数外，其它要求都不高。叶片中部的翼型厚度适中，各项气动特性也介于前两者之间。根据上述对叶片不同部位的结构域气动要求，笔者采用的多翼型叶片，选用NREL的S818、S825、S826翼型。叶根、叶中、叶尖部分分别采用S818、S825、S826翼型。

3 MW水平轴风力机风轮直径可由下式得到:

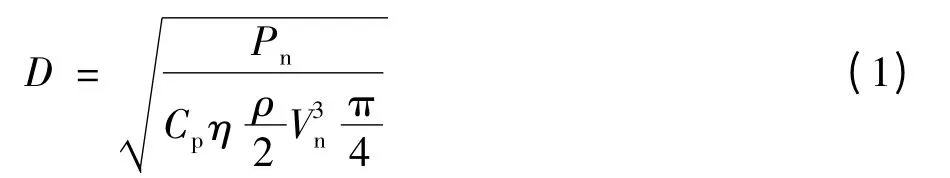
式中:D为风力机叶轮直径;Pn为风力机输出功率，取3 MW;Cp为风能利用系数，取0.345;η为传动链和发电机效率，取0.81;ρ为空气密度，取值1.225 kg/m2;Vn为额定风速，取10 m/s。目前国内外水平轴式风力机大都采用三叶片式的风轮，且三叶片的风轮输出功率较平稳，因此设计叶片数取3［2］，与叶片数为3对应的叶尖速比λ大约在5～8之间［5］，因此取λ=6。

风力机叶片的几何形状不规则，为提高风能的利用率，叶片从叶根到叶尖是由不同弦长不同扭角的叶素组成的［6］。笔者采用Wilson法对叶片进行设计，Wilson法是在Glauert法基础上做了改进，研究叶稍损失和升阻比对叶片最佳性能的影响［7］，其叶素的设计公式如下:

式中:a为轴向诱导因子;b为周向诱导因子;B为叶片数;F为普朗特修正因子;C为叶素弦长。

叶片几何参数通过Fortran编程求得，利用求得的几何参数及S818、S825、S826翼型数据在EXCEL中通过坐标变换得到叶片的三维坐标点。叶片长度为67 m，所用叶片腹板可采用过余设计得到，叶片壳厚度为100 mm，腹板厚度为100 mm。叶片叶尖小翼分别采用90°小翼和T型小翼。小翼长度取叶片长度的5%。3MW不带小翼多翼型叶片、带90°小翼叶片、带T型小翼叶片及叶片腹板模型如图1所示。

图1 3MW不带小翼多翼型叶片、带90°小翼叶片、带T型小翼叶片及叶片腹板模型

叶片材料选用环氧玻璃钢，其性能参数如表1所列。

表1 环氧玻璃钢性能参数

3 模态分析理论

模态分析用于确定设计机构部件的振动特性，如频率和振型等。如果机构本身的固有频率和外界激励频率重合，机构就会与激励一起发生共振，从而对机构造成破坏。模态分析是结构设计中重要的环节，此外动力学分析中的谱分析、瞬态动力学分析和模态叠加法谱响应分析等均要以其为前期分析过程［8-9］。

有限元离散化处理叶片，由最小势能原理可得:

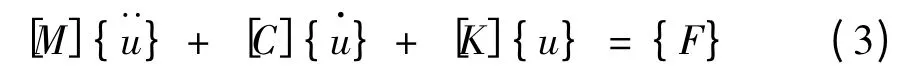
式中:［M］为叶片结构的整体质量;［C］为阻尼;［K］为刚度矩阵;{}为节点的加速度;{}为节点的速度;{u}为节点的位移;{F}为外力。

如果{F}值为“0”，在此条件下，方程有非零解，叶片处于无任何外载的自由振动状态，此时方程反应了结构的频率和振型等固有特性。在工程上，分析叶片固有特性时，通常不计阻尼，所以式(3)可简化为:

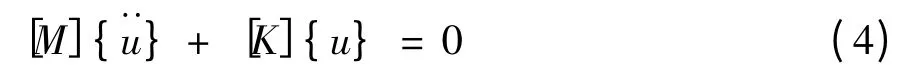
式(4)解为如下简谐运动:

式中:{U}是模态形状(无量纲位移);ω为圆周频率。

将式(5)带入式(4)得:

如式(6)中的{U}有非零解，则其系数行列式为0，即:

式中:λ=ω2，其为关于λ的多项式，根为λi=λ1，λ2……λn。将λi代入方程得:

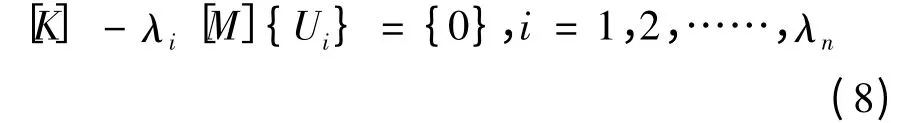
由式(8)可求得Ui即模态，fi=wi/2π为系统固有频率。

无阻尼模态分析求解基本方程是典型的求解特征值问题，如下所示:

式中:［K］为刚度矩阵;{Φi}为第i阶模态的振型向量(特征向量);ωi为第i阶模态的固有频率(特征值);［M］为质量矩阵。

风力机叶片失效主要原因之一是共振引起的断裂，为避免风力机叶片固有频率与风轮转动频率及风力机其他组件如塔架、机舱等固有频率重合，有必要对叶片进行模态分析［10］。

4 叶片模态分析

笔者对所设计的S818、S825、S826多翼型3 WM带腹板叶片进行重力预应力模态分析。利用Pro/E对叶片进行实体建模，利用Pro/E与ANSYS之间的无缝连接，将模型导入ANSYS，在ANSYS中对叶片进行重力预应力模态分析，计算出叶片的各阶振型、频率、最大变形量和最大应力。笔者计算的模态振型阶数为12阶。对带有叶尖小翼的风力机叶片进行模态分析，以确定小翼对叶片各阶振型的影响。重力预应力下90°小翼多翼型叶片模态分析如图2所示。

图2 重力预应力下90°小翼多翼型叶片模态分析

如图2所示，对于带90°小翼的多翼型叶片，其1～6阶振型主要表现为弯曲振动，7阶振型完全表现为扭转振动，8、9阶主要以弯曲振动为主，10阶则表现为弯曲振动与扭转振动的叠加形式，11阶表现为扭转振动，12阶振型则主要以弯曲振动为主。

同样，对于S818、S825、S826不带小翼的多翼型叶片，在重力预应力作用下其叶片的1～6阶振型主要表现为弯曲振动，7阶振型表现为扭转振动，8～10阶又主要以弯曲振动为主，11阶表现为扭转振动，12阶则再次以弯曲振动为主。对于S818、S825、S826带T型小翼的叶片，其1～5阶振型主要表现为弯曲振动，6阶振型完全表现为扭转振动，7、8阶振型又主要以弯曲振动为主，9～12阶振型则表现为弯曲振动与扭转振动的叠加形式。

综上所述，弯曲振动和扭转振动交替出现，低阶模态振动时主要是弯曲振动。由振动理论可知，叶片振动时，能量主要集中在1、2阶频率处，所以叶片模态振动的主要形式是弯曲振动。3种叶片前五阶的振动形式基本一样，但从第6阶开始，叶片的振动形式出现很大差异。由此可知，叶片叶尖加或不加小翼，及所加小翼的不同对叶片的振动形式有较大影响。

5 分析结果比较

重力预应力不带小翼多翼型叶片、重力预应力带90°小翼多翼型叶片及重力预应力带T小翼多翼型叶片的各阶模态频率分析比较图如图3所示。其对应的各阶模态频率分析比较表如表2所列。

从图3及表2可以看出，频率基本上随阶次的增加而增大。重力预应力作用下，带90°小翼叶片与带T小翼叶片的各阶频率略小于不带小翼叶片的各阶频率。在重力预应力作用下，不带小翼叶片的各阶频率最大，T小翼叶片的各阶频率最小。由上述结果可知，叶片叶尖加小翼可以降低叶片的振动频率，其中加T型小翼可更好地降低叶片振动频率。

图3 各阶模态频率分析比较图

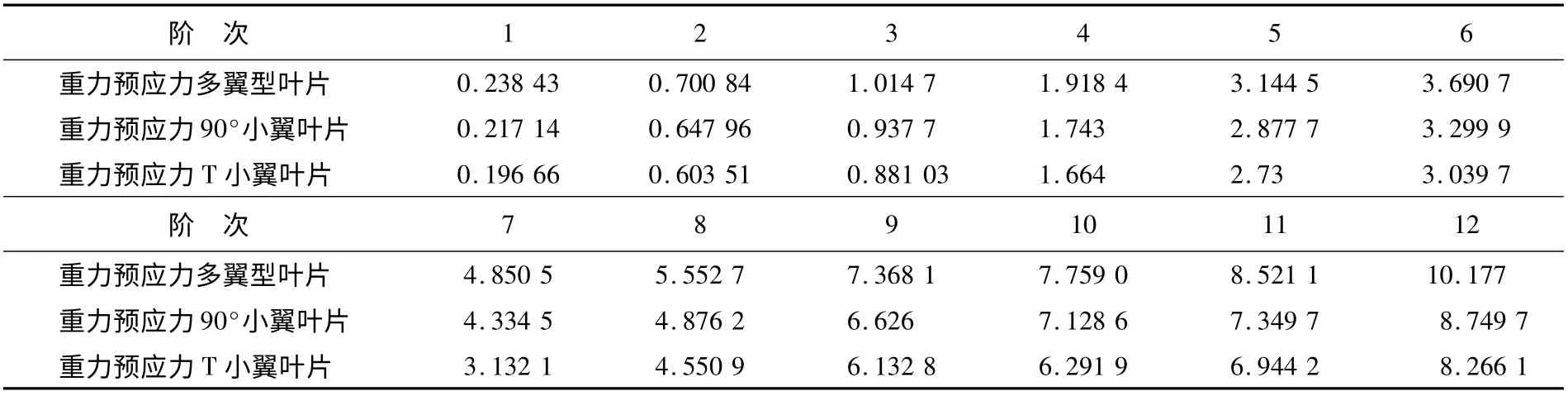
表2 各阶模态频率分析比较表

重力预应力不带小翼多翼型叶片、重力预应力带90°小翼多翼型叶片及重力预应力带T小翼多翼型叶片的各阶模态最大变形量分析比较图如图4所示。

由图4可知，在重力预应力作用下，90°小翼叶片前四阶振型的最大变形量与不带小翼叶片的前四阶振型的最大变形量相差很小;在5～12阶时，90°小翼叶片的各阶最大变形量基本都大于不带小翼叶片的各阶最大变形量。在重力预应力作用下，90°小翼叶片的各阶最大变形量基本最大，而T小翼叶片的各阶最大变形量基本最小。

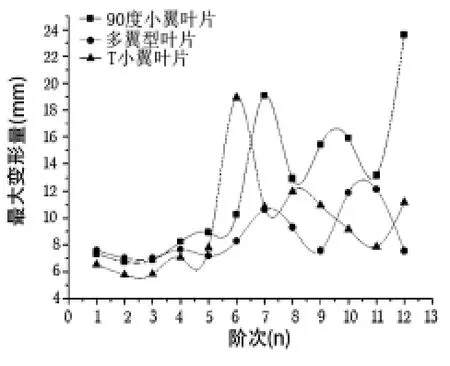
图4 各阶模态最大变形量分析比较图

重力预应力不带小翼多翼型叶片、重力预应力带90°小翼多翼型叶片及重力预应力带T小翼多翼型叶片的各阶模态最大应力分析比较图如图5所示。

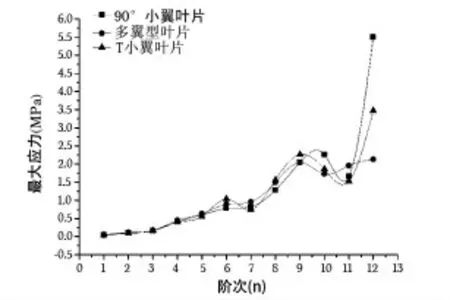
图5 各阶模态最大应力分析比较图

由图5可知，最大应力随阶次的增加而增大。在重力预应力作用下，带90°小翼叶片与带T小翼叶片前七阶振型各阶的最大预应力与不带小翼叶片的最大预应力相差不大，但8～12阶振型各阶的最大预应力却有较大幅度的增加。由此可知叶片叶尖加小翼后，对叶片各阶模态振型的最大预应力有较大影响。

6 结论

(1)在额定风速条件下，轮毂高度风的振动频率为0.8～0.9 Hz左右［11］，大于叶片的1阶振动频率。因此，笔者所选的多翼型叶片以及带小翼叶片的固有频率与风湍流的激励频率不重合，能承受复杂的工作环境，可用于3 MW风力机。

(2)叶片叶尖加或不加小翼，及所加小翼的不同对叶片的弯曲、扭转等振动形式有较大影响。

(3)在重力预应力情况下，频率及最大应力基本随阶次的增加而增大。

(4)叶片叶尖加小翼可降低叶片的振动频率，其中加T型小翼可更好地降低叶片振动频率，叶片小翼对各阶振型的最大变形量影响不大，但对叶片各阶模态振型的最大预应力有较大影响。

［1］ 曾 杰.风电场短期风速预测模型和风力机动力分析［D］.北京:华北电力大学，2009.

［2］ 陈 园.风力发电机叶片三维建模及有限元动力学分析［D］.西安:西安理工大学，2008.

［3］ 季采云，朱龙彪，朱志松，等.3MW海上风力机叶片的三维建模及模态分析［J］.机械设计与制造，2011(6):192-194.

［4］ 张智羽.带小翼的风力机叶片气动性能的数值模拟及其优化［D］.呼和浩特:内蒙古工业大学，2006.

［5］ 包 飞.风力机叶片几何设计［D］.大连:大连理工大学，2008.

［6］ 陈云程.风力机设计与应用［M］.上海:上海科学技术出版社，1990.

［7］ Friedmann.P.P.Formulation and Solution of Rotary-Wing Acrolithic Stability and Response Problems［J］.Vertival7，1980(7):101-104.

［8］ 李云松，卢 艳，刘 韵.基于设计情形的叶片模态分析［J］.机械研究与应用，2010(4):27-31.

［9］ 阿荣其其格，刘文芝.风力叶片有限元建模的两种方法［J］.机械，2009(1):48-50.

［10］ 管迪华.模态分析技术［M］.北京:清华大学出版社，1996.

［11］ Murtngh P，Basu B，Broderick B M.Along-Wind Response of a Wind Turbine Tower with Blade Coupling Subjected to Rotationally Sampled Wind Loading［J］.Engineering Structure，2005(27):1209-1219.