基于拓展的杠杆法的ZF-9HP自动变速器换挡过程分析*
2013-06-28侯国强尤明福于文涛
侯国强,尤明福,于文涛
(天津职业技术师范大学 汽车与交通学院,天津 300222)
1 ZF-9HP自动变速器结构特点
在当今汽车市场自动变速器档数主要为6档及6档以下时[1],拥有变速器最大市场份额的德国采埃孚集团公司(ZF)已经研发出专门适用于横置发动机的9HP自动变速器。它在尺寸和质量上与传统的6AT相当,但是档位数更多,换挡更加平顺。
ZF-9HP自动变速器的核心结构是4组单行星轮行星排和两个爪形离合器,两个离合器,两个制动器。如图1所示。其结构特点是第一排齿圈R1和第二排太阳轮S2连为一体,第三排齿圈R3和第一排、第二排行星架PC1、PC2连为一体,第三排行星架PC3和第四排齿圈R4连为一体,第三排太阳轮S3和第四排太阳轮S4连为一体。因此第三排和第四排是典型的辛普森结构,且第四排行星架PC4为输出构件。

图1 ZF-9HP自动变速器传动简图
6个结合元件中,爪形离合器A连接输入轴和第一排齿圈R1、第二排太阳轮S2,爪形离合器F制动第三排太阳轮S3和第四排太阳轮S4,离合器B连接输入轴和第一排太阳轮S1,离合器E连接输入轴和第三排行星架PC3、第四排齿圈R4,制动器C制动第一排太阳轮S1,制动器D制动第二排齿圈R2。
2 ZF-9HP自动变速器各档动力传递路线分析
ZF-9HP自动变速器1~5档动力传递分析时将第一排和第二排看作一个变速器,而将第三排、第四排看作另一个变速器。在一档、二档和五档时,动力流从一二排传给三四排,符合动力从前向后传递的规律。ZF-9HP自动变速器各档动力传递路线分析如表1所列[2]。

表1 ZF-9HP自动变速器各档换挡元件工作表
一档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,制动器D制动第二排齿圈R2,第二排行星架PC2减速输出至第三排齿圈R3;爪形离合器F制动第三排和第四排太阳轮S3、S4,因此第三排行星架PC3减速输出至第四排齿圈R4;因为第四排太阳轮S4被制动,所以第四排行星架PC4减速输出。一档时形成三级减速。
二档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,制动器C制动第一排太阳轮S1,第一排行星架PC1减速输出至第三排齿圈R3;爪形离合器F制动第三排和第四排太阳轮S3、S4,同理第四排行星架PC4减速输出。二档时也形成三级减速。
三档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,同时离合器B结合,将输入轴动力传至第一排太阳轮S1,因此第一排行星架PC1整体输出至第三排齿圈R3;爪形离合器F制动第三排和第四排太阳轮S3、S4,同理第四排行星架PC4减速输出。三档时形成二级减速。
四档:离合器E结合将输入轴动力传至第三排行星架PC3和第四排齿圈R4,爪形离合器F制动第三排和第四排太阳轮S3、S4,第四排齿圈R4驱动第四排行星架PC4减速输出,形成一级减速。此时虽然第三排行星架PC3会驱动第三排齿圈R3和第二排、第一排行星架PC2、PC1转动,且爪形离合器A将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,但是由于第一排太阳轮S1和第二排齿圈R2自由,所以第一排和第二排不参与动力传动。四档时形成一级减速。
五档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,同时离合器B结合,将输入轴动力传至第一排太阳轮S1,所以第一排行星架PC1整体输入至第三排齿圈R3,又因为离合器E将输入轴动力传至第三排行星架PC3和第四排齿圈R4,此时第三排太阳轮S3整体输出,即第四排太阳轮S4也与输入轴同速,最终第四排行星架PC4整体输出。五档时为直接档。
ZF-9HP自动变速器6~9档和R档时,将第一排和第二排组成的变速器看作一个制动器,部分约束第三排齿圈,因此引入矢量表示法[3]。如图2所示,A、B、C分别代表太阳轮、行星架和齿圈;线段AB、BC、AC分别表示齿圈、太阳轮和行星架齿数。在单级行星排中用单箭头的线段表示构件的转速和方向。可得到一个构件固定的情况下,其它两个构件的转动情况。
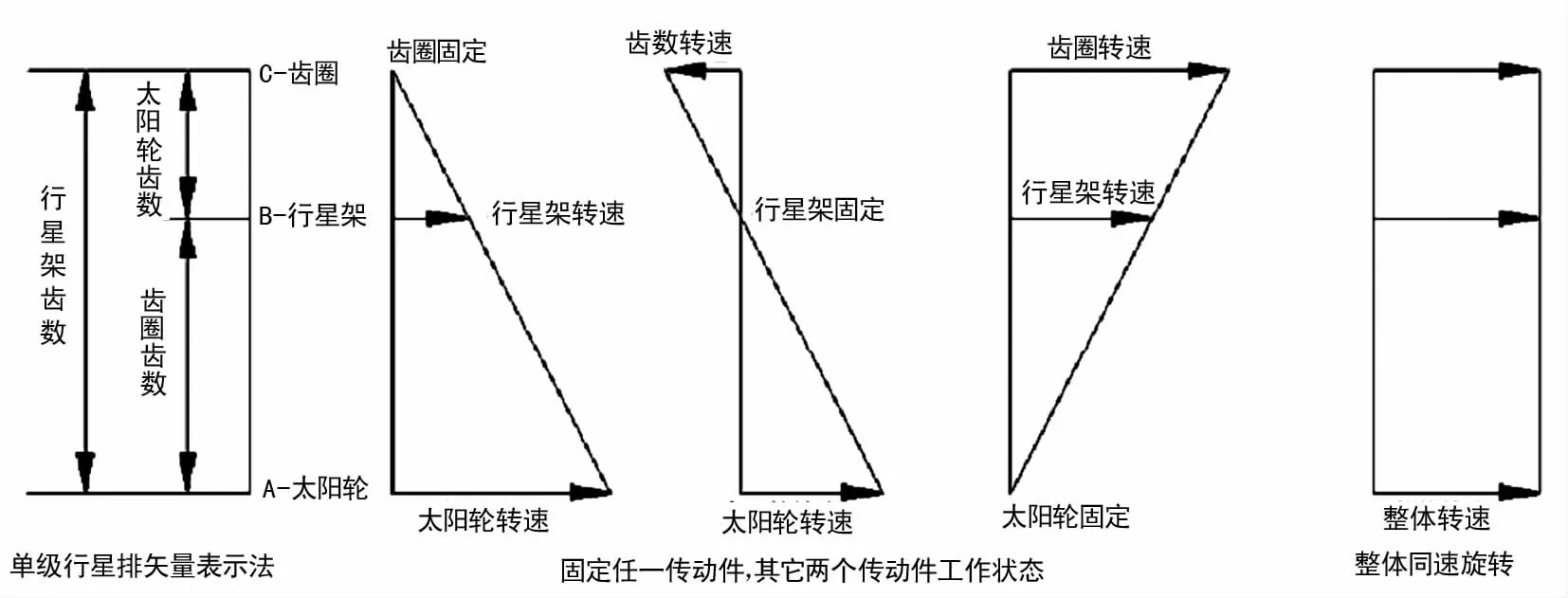
图2 用矢量表示单级行星齿轮机构运动规律
同时通过矢量表示法可以很容易理解三个构件同时旋转但转速和方向各异的情况。如图3所示,当齿圈和行星架转速相同时,将驱动太阳轮同速输出;当齿圈转速减少、为零甚至逆转而行星架转速不变时,太阳轮转速将增加。因此得ZF-9HP自动变速器6~9档和R档动力传递分析如下:

图3 行星架转速不变,减少齿圈转速达到增大太阳轮转速目的图示
六档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,制动器C制动第一排太阳轮S1,第一排行星架PC1减速输出至第三排齿圈R3;离合器E结合,将输入轴动力传至第三排行星架PC3和第四排齿圈R4,由于第三排是两个输入,一个输出的工作情况,所以由矢量表示法可知第三排太阳轮S3增速输出,即第四排太阳轮S4增速输出;又由于第四排齿圈R4与输入轴转速相同,所以第四排也为两个输入,一个输出的工作情况,因此第四排行星架PC4增速输出。
七档:爪形离合器A结合,将输入轴动力传至第二排太阳轮S2和第一排齿圈R1,制动器D制动第二排齿圈R2,第二排行星架减速输出至第三排齿圈R3;离合器E结合,将输入轴动力传至第三排行星架PC3和第四排齿圈R4,由于第三排是两个输入,一个输出的工作情况,所以由矢量表示法可知第三排太阳轮S3增速输出,即第四排太阳轮S4增速输出;同理 第四排行星架PC4增速输出。
八档:制动器C制动第一排太阳轮S1,制动器D制动第二排齿圈R3,则第一、第二排相当于被制动,所以第三排齿圈R3转速为0。离合器E结合,将输入轴动力传至第三排行星架PC3和第四排齿圈R4,第三排太阳轮S3增速输出,即第四排太阳轮S4增速输出;同理第四排行星架PC4增速输出。
九档:离合器B结合将输入轴动力传至第一排太阳轮S1,此时第一排行星轮逆转,驱动第一排齿圈R1逆转,即第二排太阳轮S2逆转,制动器D制动第二排齿圈R2,所以第二排行星架PC2逆转输出至第三排齿圈R3;离合器E结合将输入轴动力传至第三排行星架PC3和第四排齿圈R4,由于第三排是两个输入,一个输出的工作情况,所以由矢量表示法可知第三排太阳轮S3增速输出,即第四排太阳轮S4增速输出;同理第四排行星架PC4增速输出。
倒档:离合器B结合将输入轴动力传至第一排太阳轮S1,制动器D制动第二排齿圈R2,与九档时相同第二排行星架PC2逆转输出至第三排齿圈R3;爪形离合器F结合制动第三排太阳轮S3和第四排太阳轮S4,因此第三排行星架PC3减速逆转;同理第四排行星架PC4减速逆转。
以上所述减速、整体输出、增速均相对输入轴转速而言。
3 ZF-9HP自动变速器拓展的杠杆法分析
3.1 杠杆法简介[4]
一个行星排由太阳轮S、行星轮、齿圈R和行星架PC组成。根据其结构特点,将一个行星排等效为一个垂直杠杆和3个支点,3个支点分别代表太阳轮S,行星架PC和齿圈R。对于单行星轮行星排,支点S和R距支点PC的长度(力臂)分别与齿圈齿数Zr和太阳轮齿数Zs成正比,图中k为任意比例系数。单行星轮行星排和双行星轮行星排的等效杠杆图分别如图4所示,(a)、(b)两图的主要区别在于齿圈位置不同。

图4 等效杠杆图
多行星排并联时,每个行星排视为一个垂直的杠杆和3个支点,行星排之间的构件相互连接,在杠杆图上视为各支点之间的连接。在处理时根据需要,既可以将杠杆重叠,又可以将杠杆分开。重叠时将相互连接的部分合并为一个点,分开时连接点用一水平线表示。两种情况都要对杠杆的力臂进行调整,调整时要保证连接部分合并点之间的力臂长度相等,并且各杠杆力臂长度比不变,在这种由多个行星排杠杆图合并的总杠杆图上标上离合器、制动器,以及输入构件(i)、输出构件(o),即得多行星排并联等效杠杆图。
3.2 拓展的杠杆法介绍
原有的杠杆法在分析传动方案时,前提是行星齿轮机构的各个构件都能进行制动或作为动力的输入元件,它对于传动方案中的两排行星排机构进行分析方法是可行的,但随着6速甚至更多档位数自动变速器的诞生,将采用更多行星排,如ZF-9HP自动变速器机械传动部分由4个单行星轮行星排组成,以至于原有杠杆法在分析传动方案时失去了作用。基于此,笔者在原有辛普森式两排行星齿轮机构的等效转速线图中加入了K1、K2和-K′轴三条输入转速线。此K1、K2和-K′轴输入线很好的反映了在辛普森式两排行星齿轮机构(即第三排和第四排)的基础上再前加两排单行星轮行星排的目的,也即提供了多种不同的输入轴转速。Ki的取值取决于多加的且参与传动的行星排的输出转速与输入转速之比。
3.3 ZF-9HP自动变速器换挡过程分析
图5为根据ZF-9HP自动变速器传动简图绘制的等效杠杆图[5]。由图4、图5分析可知原有的杠杆法难以满足ZF-9HP自动变速器的分析研究,故笔者对原有的杠杆法进行了拓展,新拓展的等效杠杆转速线图如图6所示[6-7],在图6中可以清晰地看出ZF-9HP自动变速器各档位下的转速关系和作用元件。图示x轴表示行星排中各构件转速的大小和方向,y轴代表各固定构件的转速。K2代表一档时第二排行星架PC2减速输出后的输出转速与输入转速之比,K1代表二档时第一排行星架PC1减速输出后的输出转速与输入转速之比,-K'代表九档和倒档时第二排行星架逆转输出的输出转速与输入转速之比。a为第四排齿圈齿数和太阳轮齿数之比,(1+a)/b为第三排齿圈齿数与太阳轮齿数之比。

图5 ZF-9HP自动变速器等效杠杆图
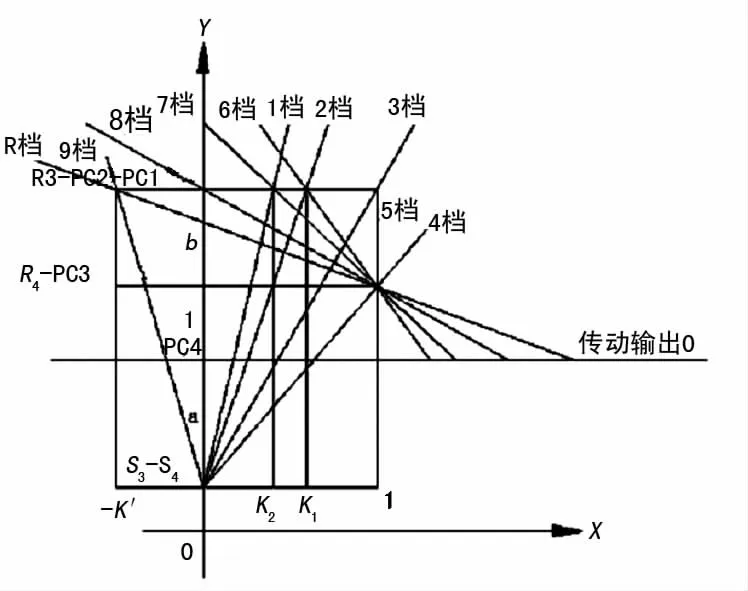
图6 ZF-9HP自动变速器等效杠杆转速线图
由图6得出2ZF-9HP自动变速器各档传动情况如表2所列。

表2 ZF-9HP自动变速器各档传动情况
根据表中1档、2档、4档、8档和R档可分别算出a=2.63 158,b=1.38 095,K2=0.39 963,K1=0.67 025,K′=0.50 269。再将计算所得数据分别代入3档、4档、6档、7档、9档,验证统计得i3=1.91 022、i4=1.38 229、i6=0.80 724、i7=0.69 698、i9=0.47 889。
计算出的传动比值和表1中给出的传动比值吻合。
本文利用拓展的杠杆法分析ZF-9HP自动变速器的换挡过程完全正确可行。同时5~9档及倒档转速线的变化,也形象的表达了矢量表示法的原理。
4 结论
ZF-9HP自动变速器拥有4个减速档、1个直接档、4个超速档和一个倒档,满足了当今汽车市场自动变速器多档化的要求,由表1可以看出ZF-9HP自动变速器各档齿比间隔更小,同时ZF-9HP自动变速器的控制元件组合逻辑非常巧妙,无论是顺序换挡还是隔档换挡都只需两个换挡元件动作,因此换挡更平顺。档位数的增加并没有导致机械传动部分体积和质量的增加,例如第一、第二行星排实际在同一个平面内,故与ZF-6HP自动变速器相比长度不变。此外通过分析并对其拓展,再一次证明了杠杆法在分析自动变速器换挡过程中较解析法和图论法更直观、便利,也为今后其他自动变速器的分析和设计提供了很好的启示。
[1] Chirs R,Ciesia M J.Jennings Am Ocular Apporach Power—train Modeling and Shift Quality Analysis[J].SAE Paper,1995(2):238-246.
[2] 罗新闻.德国采埃孚9HP自动变速器结构及动力传递路线分析[J].汽车维修与保养,2013(7):77-80.
[3] 吴泽辉.解析德国采埃孚九速自动变速器[J].汽车维修与保养,2013(6):88-90、93.
[4] 黄宗益.现代轿车自动变速器原理和设计[M].上海:同济大学出版社,2006.
[5] 何国旗,谭放鸣,王绍良,等.利用等效杠杆法分析自动变速器行星齿轮传动[J].机械传动,2006,30(1):69-73.
[6] 李志伟,尤明福,文 强.基于杠杆法分析01M自动变速器的换挡过程及设计思路[J].机械传动2011(10):50-53.
[7] 尤明福,李志伟,甘 伟,等.基于杠杆法的8速自动变速器传动方案的设计[J].中国机械工程,2012(12):112-115.
