基于Fluent的AY型离心油泵叶轮内流场数值模拟*
2013-06-28魏佳广张智宇邵亮亮赵福臣刘立国
魏佳广,张智宇,邵亮亮,杨 成,赵福臣,刘立国,王 强
(1.海洋石油工程股份有限公司,天津 300452;2.中国石油天然气股份有限公司 辽阳石化分公司,辽宁 辽阳 111003;3.海洋石油工程(珠海)有限公司,珠海 广东 519050;4.中海石油华鹤煤化有限公司,黑龙江 鹤岗 154102;5.中航黎明锦西化工机械(集团)有限责任公司设计研究院,辽宁 葫芦岛 125001)
1 引言
离心泵作为石油储存和运输工程(包括船舶调载泵等)中的动力源,其结构简单、运转平稳、操作方便、易于维护,故在石油行业占有非常重要的地位。离心泵是炼油厂和化工厂主要的流体输送设备,离心泵节能与经济效益的提高,对电能的节约和国民经济的发展起着举足轻重的推动作用,所以如何提高离心泵的实际工况点效率是各科研院校和设计院的研究重点。
笔者通过对离心泵叶轮工作过程和结构的分析,考虑整个叶轮为对称结构,建立叶轮单个叶道的简化模型和叶轮整体的三维模型,并进行网格划分。利用Fluent软件进行流动分析,对离心泵叶轮模型内部流场进行三维数值模拟,初步分析离心泵叶轮的速度及压力分布,获得离心泵叶轮流道的速度场、压力场,且充分了解叶轮内部复杂的流场结构,为深入了解离心泵内部流动规律提供了理论依据[1]。
2 流体流动基本控制方程及定界条件
2.1 连续方程
连续性方程描述了流体流动过程中流体质量守恒的性质。直角坐标系下的连续性方程表示为[2]:
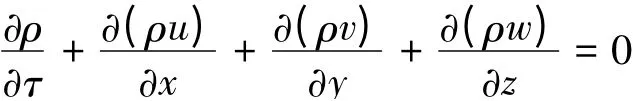
2.2 湍流模型[3]
标准k-ε模型的湍动能k和耗散率ε方程如下所示:
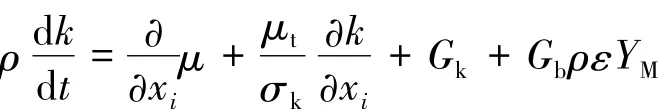
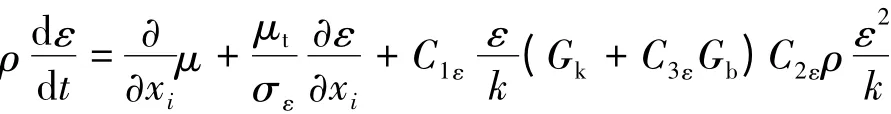
式中:Gk为由于平均速度梯度引起的湍动能产生;Gb为由于浮力影响引起的湍动能产生;YM为可压缩湍流脉动膨胀对总的耗散率的影响;μt为湍流粘性系数,μt=ρCμ(k2/ε)。
在Fluent中,作为默认值常数,C1ε=1.44,C2ε=1.92,C3ε=0.09,湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0,σε=1.3。
2.3 定界条件
为确定控制方程的解还需给出定解条件。流场计算所需要的边界条件主要有:
(1)进口边界:一般要求给出叶轮进口的速度、压力、密度或相应的相容条件。在此给出进口速度,压力在进口截面假设均匀分布。
(2)出口边界:一般取充分发展的库塔(Kutta)条件或由上游的速度推算而得。
(3)固壁边界:对于考虑粘性的控制方程,固壁上流体质点满足无滑移条件,即令壁面速度W=0。固壁为绝热条件,叶轮为转动边界,顺时针方向,转速为2 950 r/min,在临近固壁的区域采用了壁面函数,叶片表面、前后盖板等固壁均为无滑移、绝热壁面条件。
(4)周期性边界:即叶片的压力面与吸液面的速度、压力相等、液流角相等[4]。
3 叶轮建模
本研究的设计参数见表1所列。叶片数为4片的离心泵进行参数化设计,将得到图1~2的轴面投影图及模型截线图[5]。

表1 离心泵叶轮设计参数
利用Pro/E软件绘制叶片三维立体图,叶片模型如图1所示。扭曲叶片建好后,即可进行叶轮实体造型,将叶轮分为前盖板(图3所示)、后盖板(图4所示)和叶片3个部分,画出3个部分实体后,利用Pro/E中的装配功能对三维叶轮进行组装。图5为带有前后盖板的叶轮模型,利用叶轮三维实体模型[6],可进行流场的数值模拟等。

图1 叶片模型裁剪图

图2 叶片三视图

图3 叶轮上盖板

图4 叶轮下盖板

图5 叶轮三视图
4 叶轮流道网格建模
由于叶轮按照4个叶片设计,即叶轮有4个流道,叶轮[7]是轴对称分布,可节约建模时间、流道网格划分时间以及流道数值模拟时间。能只对其中一个流道进行建模和网格划分,以及最终进行流体数值模拟,希望这种方法能够在离心泵叶轮设计中得到广泛应用,流道模型如图6、7所示。

图6 叶轮单流道三维实体

图7 叶轮流道三维实体
笔者运用了分块网格技术将离心泵叶轮内通道求解区域划分成若干较为简单的块,在各块中分别生成网格。各区网格可根据其区域和流场的特点,灵活选择合适的拓扑结构,并安排疏密分布,提高结构格处理复杂外形的能力,从而降低了网格生成的难度,生成了贴体及与边界正交的高质量的结构化网格。此处采用贴体坐标下的有限体积法求解雷诺。
平均N-S方程,应用标准k-ε紊流模型加壁面函数法对离心水泵叶轮内部典型工况下的三维紊流流动进行了详细的数值计算与分析,获得了合理的流速和压力分布。
由于流道的形状比较复杂,叶轮入口和前后盖板处流道最窄,叶轮出口和前后盖板处流道最宽,两者相差很大。如果选用相同的单元尺寸,当单元尺寸过大计算结果会存在较大误差,若尺寸过小,则计算时间变得很长。故不同的面选用不同的单元尺寸,叶轮入口和前后盖板靠近的区域,采用的单元尺寸为小值;叶轮出口和前后盖板处选用较大尺寸的单元。对拐角区域进行细化,拐角区域单元尺寸取小值。通过对单元尺寸的控制,从而保证合理的计算精度和计算时间。网格生成质量对计算精度与稳定性影响极大,使用Tet/Hybrid元素和Tgrid类型对流道进行网格划分,为了使计算结果接近实际情况,把网格划分为1 610 787个单元。网格如图8、9所示。
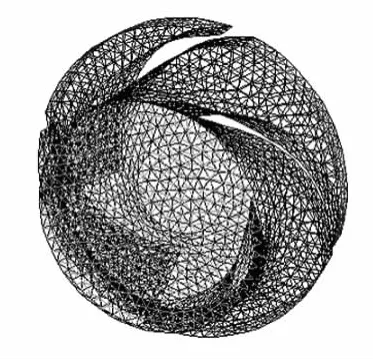
图8 流道壁面网格图
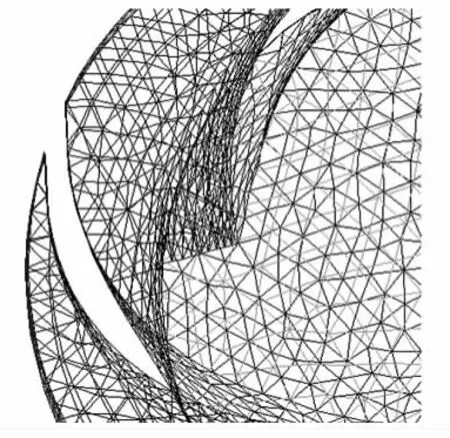
图9 壁面网格放大图
5 叶轮流道数值模拟
针对流道内速度分布和压力分布进行分析,流量和压力参数的设定取操作工况下的流量和压力,流体采用常温水。把Gambit生成的网格导入到Fluent里进行流场计算。计算时采用三维定常湍流计算方法。
对控制方程的离散采用如下格式:动量、湍动能和湍流扩散率系数项采用二阶迎风格式,压强项采用标准格式,压力速度耦合方法选用SIMPLY算法。
边界条件:入口设置velocity inlet设计流量下流速为3.015 5 m/s,入口速度垂直入口整个面,出口设置为outflow。流道和壁面设置转速为2 950 r/m,转动方向为顺时针方向。流道连续性条件设置为水[8-9]。
流场计算结果:经过825次迭代,计算收敛,流道内流体的速度分布情况如图10~12所示。

图10 叶轮单流道速度分布图

图11 叶轮流道速度分布图
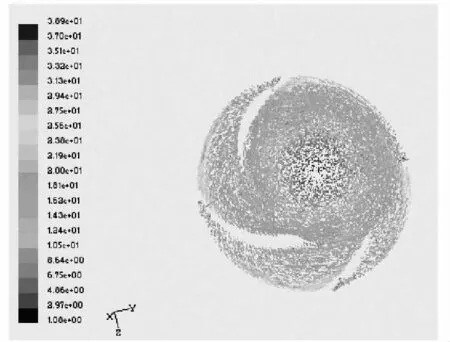
图12 叶轮流道速度矢量图
从上图中可看出叶片出口工作面的速度大于叶片背面的速度,叶轮出口工作面和叶片背面之间速度梯度比较平缓,从叶轮入口到出口速度梯度沿半径逐渐增大,上盖板的速度大于下盖板速度。同时叶片包角减小至90°,适应叶轮外径减小的情况,保证叶片出口处为直叶片,满足操作工况点的要求,水利损失相对改进前大大减小,整个流道流体的速度从小到大平稳过渡,没有回流和涡流产生,接近理论流体流动状况[10]。
流道内流体的压力分布情况如图13、14所示。可以看出,叶轮流道入口处压力在整个流道中最小,叶片入口的工作面压力大于背面压力。该区域为整个叶轮中的压力最小处,由于在设计过程中按照高汽蚀设计方法设计叶片入口宽度b值,同时该泵为正压吸入,这里就剔除了发生汽蚀的可能性。工作面的压力沿流道一直都大于叶片背面的压力,在工作面的出口处为压力最高点,出口压力符合设计要求[11]。
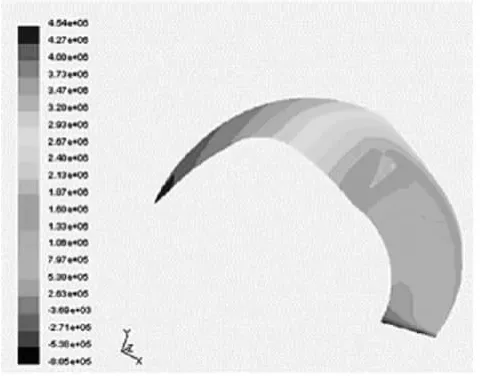
图13 叶轮单流道绝对压力分布图
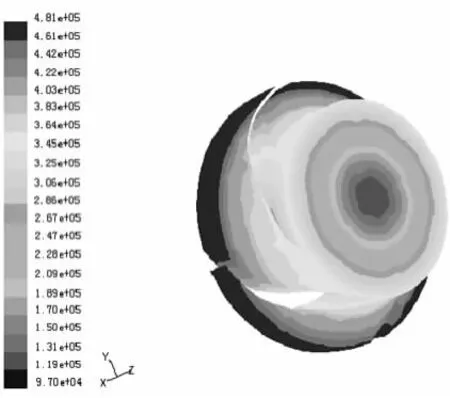
图14 叶轮流道绝对压力分布图
6 结论
通过对原型离心泵叶轮通道内流动进行CFD分析后将会发现,在原型离心泵进口处具有头部撞击,叶片工作面压力过大,叶片背面压力较小,且有环流出现,说明叶轮翼型安放角度不合理。提出了三维紊流数值分析基础上的离心泵叶轮参数优化方法。主要有以下几方面。
(1)改进叶片的入口角,使之适应来流条件,达到进口无撞击。
(2)改变叶片型线,也就是调整叶片不同位置的曲率半径,使流体通过流道时受力变化均匀,流道内压力变化趋势更为明显,叶轮运行更加稳定。
采用计算机数值模拟能准确地找出发生水力损失的具体部位并掌握损失的产生机理,进而针对性的解决此问题,并通过修改设计来完善产品性能,使效率大大提高。说明CFD分析技术已成为流体力学中最具活力的部分,成为设计和优化离心泵等流体机械的重要工具[12]。
[1] 李龙陈,黎 明.泵优化设计国内现状及发展趋势[J].水泵技术,2003(3):8-11.
[2] 韩占忠,王 敬,兰小平.Fluent流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2004.
[3] 江 帆,黄 鹏.Fluent高级应用与实例分析[M].北京:清华大学出版社,2008.
[4] 李 巍,王国强,刘立军.离心叶轮内三维紊流流动数值模拟[J].上海交通大学学报,2000,34(1):143-147.
[5] 离心泵设计基础编写组.离心泵设计基础[M].北京:机械工业出版社,1974.
[6] 李 春,倪建华,苏 进.离心泵叶轮叶片三维参数化造型技术研究[J].水泵技术,2003(2):22-25.
[7] 宋天民,孙 铁,谢禹钧.炼油厂动设备[M].北京:中国石化出版社,2006.
[8] 李文广.离心泵叶轮内部流动数值解的评价[J].水利学报,1999(12):40-44.
[9] 刘立军,徐 忠.离心叶轮内部三维湍流流场的数值分析[J].工程热物理学报,1996,17(3):296-300.
[10] 钱锡俊,陈 弘.泵和压缩机[M].东营:石油大学出版社,2007.
[11] Naoki Matsushita,Akinori Furukawa,Satoshi Watanabe,et al.Study on Design of Air-water Two-phase Flow Centrifugal Pump Based on Similarity Law[J].International Journal of Fluid Machinery and Systems,2009,2(2):42-45.
[12] YUAN Shouqi,NI Yongyan,PAN Zhongyong,et al.Unsteady Turbulent Simulation and Pressure Fluctuation Analysis for Centrifugal Pumps[J].Chinese Journal of Mechanical Engineering,2009,22(1):342-346.
