基于MATLAB等节距圆锥螺旋弹簧的刚度分析*

任晋贤

(中北大学 材料科学与工程学院，山西 太原 030051)

1 引言

螺旋弹簧在振动控制、限位装置、复位机构中应用十分广泛，因为其具有良好的柔性、通过吸收和释放机械能来达到减振与缓冲的作用。在螺旋弹簧中，圆锥螺旋弹簧按结构分为等节距型和等螺旋角型，笔者主要研究等节距圆锥螺旋压缩弹簧。由于圆锥螺旋弹簧的载荷和变形间是非线性关系，设计变量运算较繁琐，所以用计算机辅助设计十分必要［1］。

如图1(a)中，R2为弹簧的大圈半径，d为簧丝直径，H0为压并高度［2］。如图1(b)所示，等节距圆锥螺旋弹簧在底面上的投影为阿基米德螺旋线，θ为这种螺旋线的极角，由图可以看出，该螺旋线的极角θ每增加2π，半径R增加t×tanψ/2(t为弹簧节距，ψ为弹簧圆锥角)。由此可以得到等节距圆锥螺旋压缩弹簧的半径表达式为:

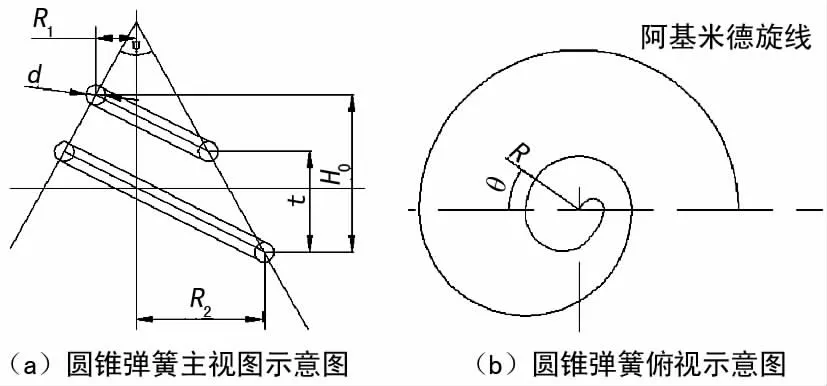
图1 圆锥螺旋压缩弹簧几何参数

式中:R1为弹簧的小圈半径。

2 等节距圆锥螺旋压缩弹簧的刚度分析

(1)等节距圆锥压缩弹簧开始有弹簧圈接触前的变形计算

由于压缩弹簧的螺旋角比较小，当弹簧受到轴向载荷P后，根据弹簧设计手册得到接触前的变形为:

式中:n为弹簧的有效圈数;G为剪切模量。

(2)等节距圆锥压缩弹簧开始有弹簧圈接触后的变形计算

对于等节距为t的圆锥压缩螺旋弹簧，开始接触的弹簧圈为i的变形为:

弹簧的变形同样分为弹簧圈压并部分和未压并部分。未压并部分的变形由式(2)可知为F1，压并部分的变形为F2，根据式(3)得:

从而得到等节距圆锥压缩螺旋弹簧在弹簧圈i开始压并时，整个弹簧的总变形为:

由式(2)、(4)可知，等节距螺旋压缩弹簧载荷和位移的变化是一个非线性的变值。

3 结果与讨论

3.1 数据处理

现在以某隔振器的关键部件锥簧为例，其参数如下:有效圈数n=4，大端半径R2=18 mm，小端半径R1=9 mm，节距t=3 mm，簧丝直径d=2.3 mm，剪切模量G=78 400 N/mm2。运行MATLAB编程，并对数据加以处理，可得圆锥弹簧的特性曲线。

由图2可知，i表示从大端开始第i圈开始接触，因为等节距圆锥压缩弹簧压并过程中，通过将i在0到4取值，当位移Fi＜4.7 mm时，特性曲线为直线，载荷和位移表现为线性关系，当Fi＞4.7 mm时，特性曲线为非线性关系，随着接触的弹簧圈数增加，其刚度逐渐增加，表现为很强的硬特性。当所有弹簧圈完全压并时，位移为10 mm，载荷为117.6 N。

图2 算例圆锥压缩弹簧特性曲线

3.2 数据的曲线拟合

曲线拟合又称为函数的逼近，是一种近似求解函数的数值方法，它不要求近似函数在函数节点处与函数值相等，只要求尽可能地反应函数的基本走势［5-6］。等节距圆锥弹簧的特性曲线函数由于过于繁杂，通过运用MATLAB应用程序，将其特性曲线拟合成为简单的代数多项式。为振动分析与隔振设计提供简单的数学模型。

执行拟合程序后，得到图3所示的曲线图，其中拟合三次多项式曲线与原函数偏差较大，而拟合五次多项曲线与原函数基本重合，偏差较小。可得出，拟合多项式次数越高，表示曲线的精度越精确，但数学模型越复杂。在振动与隔振分析中，权衡各种因素选择合适的数学模型。其中三阶的拟合多项式曲线函数关系如下:

图3 3条曲线对比图

3.3 簧丝直径对特性曲线的影响

当簧丝直径分别取2.3 mm、2.5 mm、2.7 mm、2.9 mm、3 mm时，作出的特性曲线图4所示。

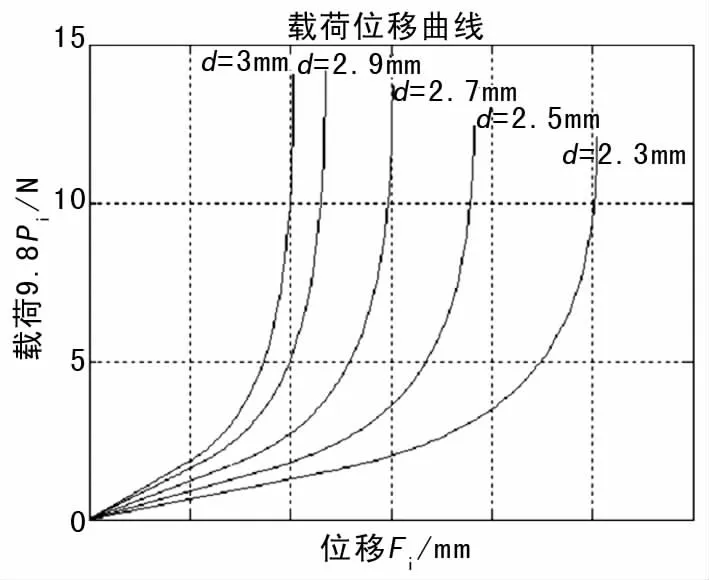
图4 等节距锥弹簧簧丝取不同直径时的载荷位移图

由图4得，随着簧丝直径变大，锥弹簧的硬特性表现就越强，刚度越大，开始接触时的载荷没有明显变化，但是开始接触时的位移变小了，压并时的载荷增加，但压并时的位移明显减小。

4 结论

(1)等节距螺旋压缩弹簧开始接触前的刚度曲线是直线，接触后的刚度曲线是非线性的。而且表现出很强的硬特性。

(2)运用MATLAB程序设计语言，可以得出圆锥弹簧的特性曲线，拟合后的多项式函数关系更为简单，为振动分析提供了简单的数学模型。

(3)簧丝直径越大，圆锥弹簧的硬特性越强。

［1］ 杨 铭.某型号隔振器的弹簧设计［J］.南京工程学院学报(自然科学版)，2009，7(1):26-27.

［2］ 程 浩.节距圆锥螺旋压缩弹簧计算机辅助设计［J］.计算机应用技术，2009，36(5):44-46.

［3］ 成大先.机械设计手册［M］.北京:化学工业出版社，2004.

［4］ 张英会，罗圣国，郭荣生，等.弹簧手册［M］.北京:机械工业出版社，1982.

［5］ 张德丰.MATLAB数值计算方法［M］.北京:机械工业出版社，2010.

［6］ 刘国初.复合弹簧的创新设计［J］.机械，2012(4):67-69.