零级随机Dirichlet级数的增长性

张海侠

(许昌学院数学与统计学院,河南许昌461000)

零级随机Dirichlet级数的增长性

张海侠

(许昌学院数学与统计学院,河南许昌461000)

研究了当随机变量满足一定条件时,全平面上零级随机Dirichlet级数的增长性,得到了关于它们增长性的两个定理.

Dirichlet级数；零级；增长性

1 引言和引理

关于Dirichlet级数的增长性,已取得许多研究成果.对于零级Dirichlet级数和零级随机Dirichlet级数,由于其自身的特殊性,仍有许多问题没有解决.本文在较弱条件下,得到了全平面上零级随机Dirichlet级数的增长性的两个定理.考虑随机Dirichlet级数

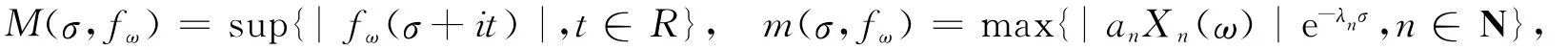
考虑相对应的Dirichlet级数

若级数(3)满足条件(2),则和函数f(s)表示一个正函数.记M(σ,f),m(σ,f)分别为f(s)的最大模与最大项.

如果,则称级数f(s)为零级Dirichlet级数.

引理1［2］设M(x)为正值连续函数且趋于∞,满足

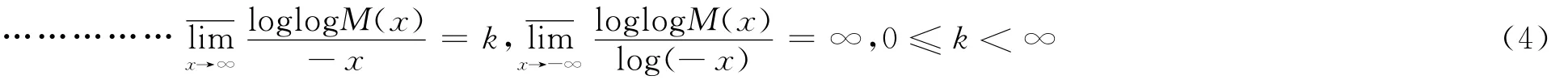
则存在连续可微函数U(―x),满足如下条件：

(ii)U(―x)单调趋于∞,且log U(―x)/log(―x)趋于∞.

(iii)对任意的t＞0,U(―(t+1)x)≤((t+1)k+O(1))U(―x).

利用文献［3］中的证明方法类似可证如下引理.

引理2 若级数(3)满足条件(2),(4)和

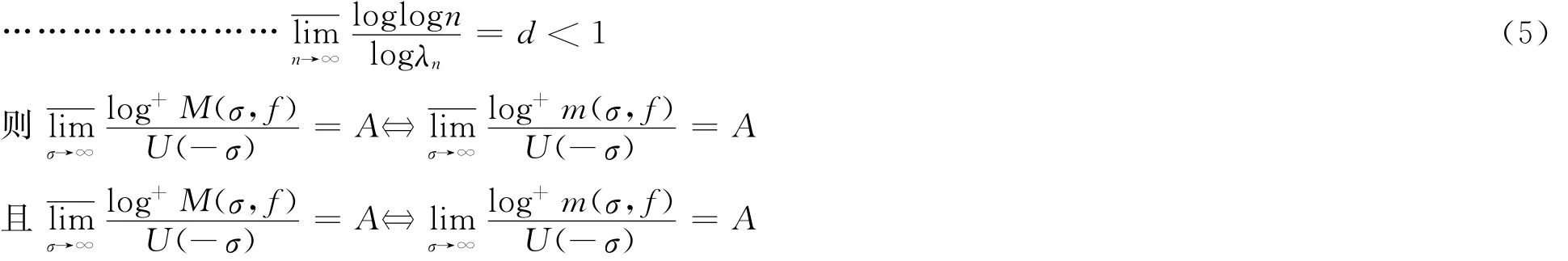
引理3 若级数(3)满足引理2的条件,则

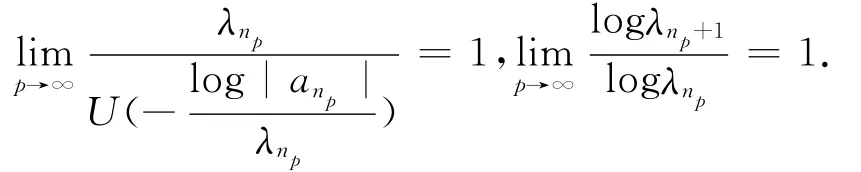
引理4［4］若概率空间(Ω,F,P)上的一列复随机变量满足条件：存在常数α＞0,β＞0,使得,那么对几乎所有的ω∈Ω,存在N(ω),当n＞N(ω)时,有

2 定理及其证明

定理1若零级随机Dirichlet级数(1)满足条件(2),(5)和引理4的条件,并且

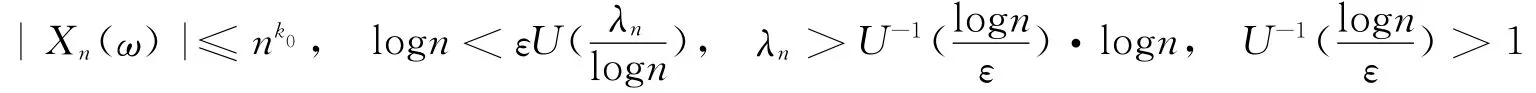
因此

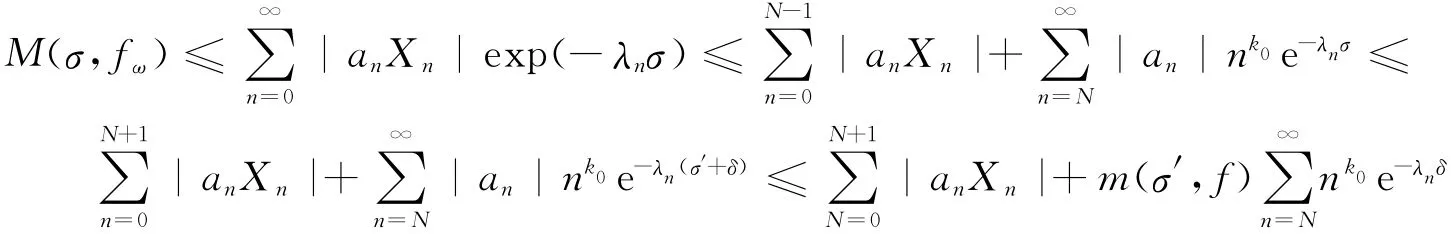
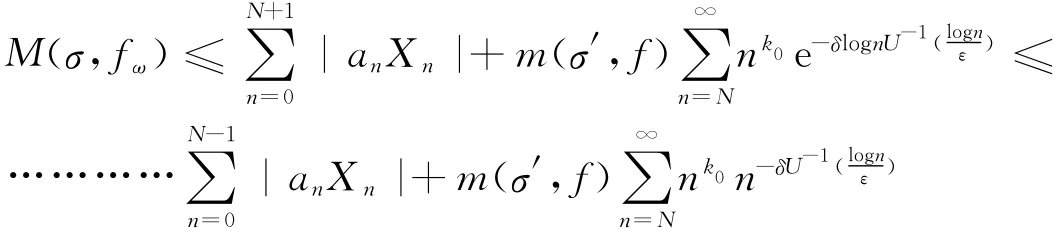
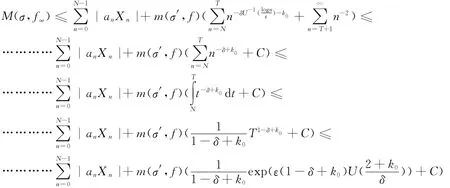
其中C为正常数.于是就有

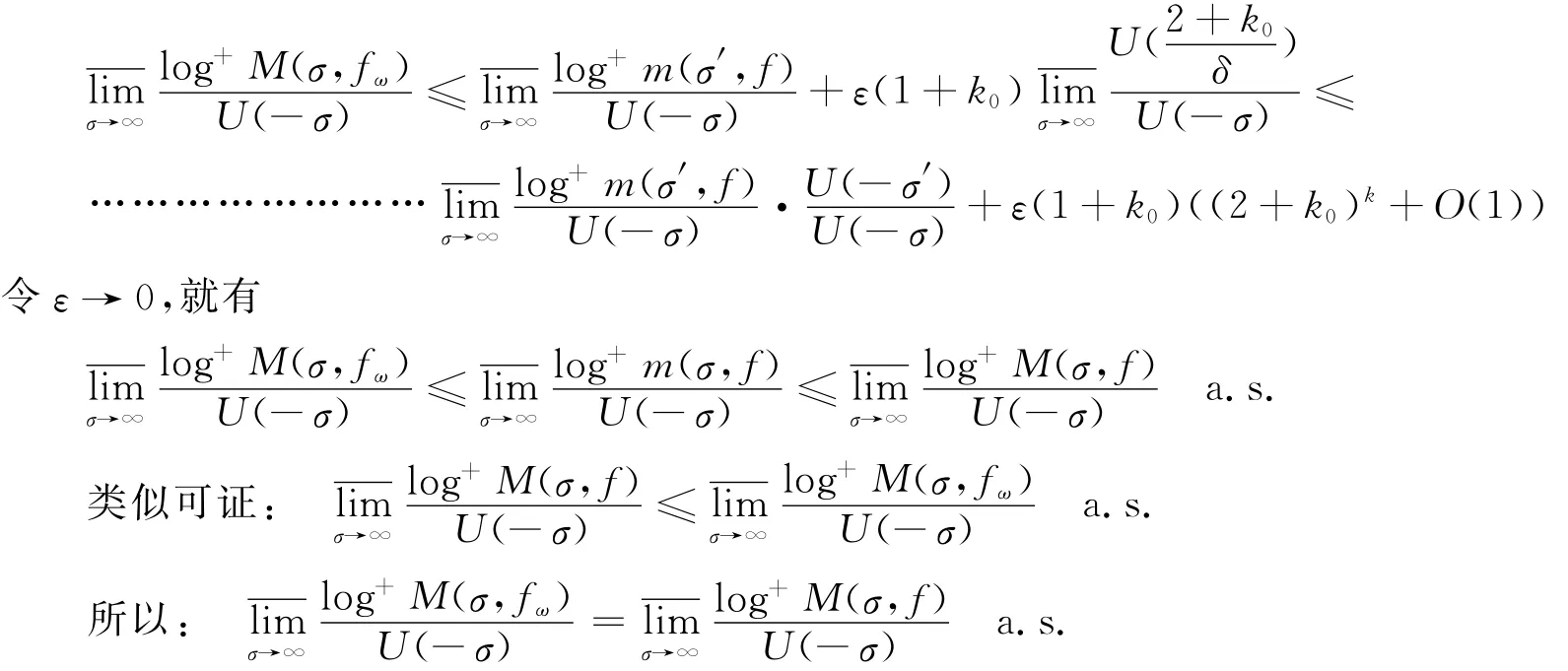
于是定理得证.

定理2 若零级随机Dirichlet级数(1)满足定理1的条件,则

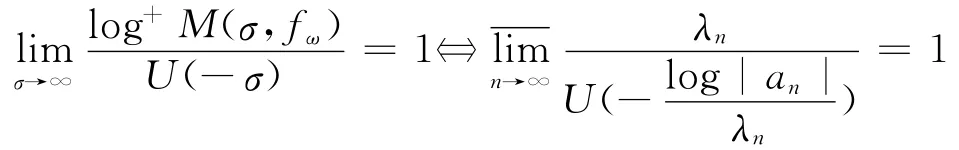
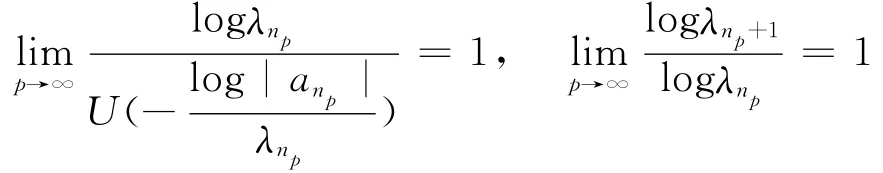
证明 首先证明若零级随机Dirichlet级数(1)满足条件(5)和引理4中的条件,则∀ε＞0,几乎必然对所有的,存在正常数),使得

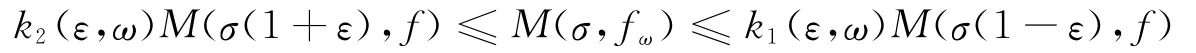
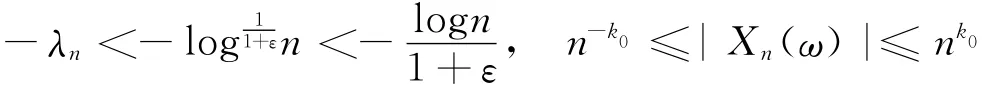
于是

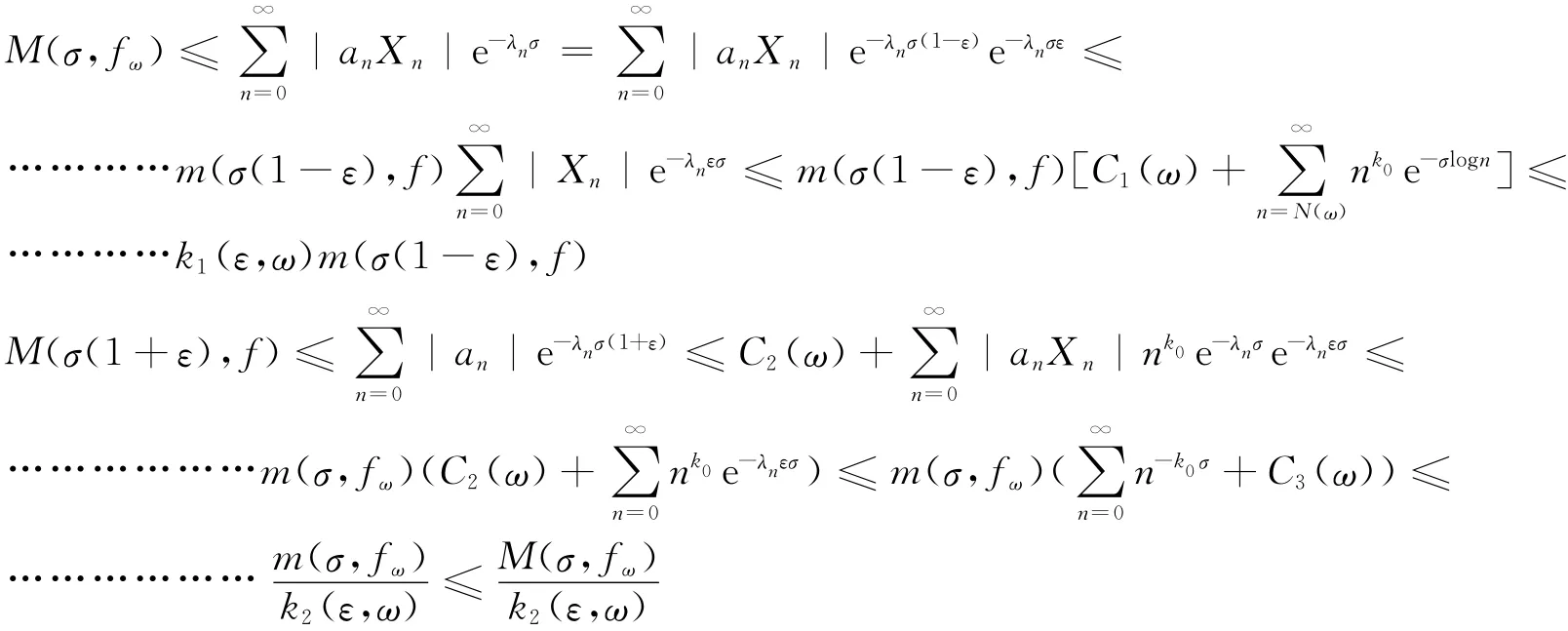
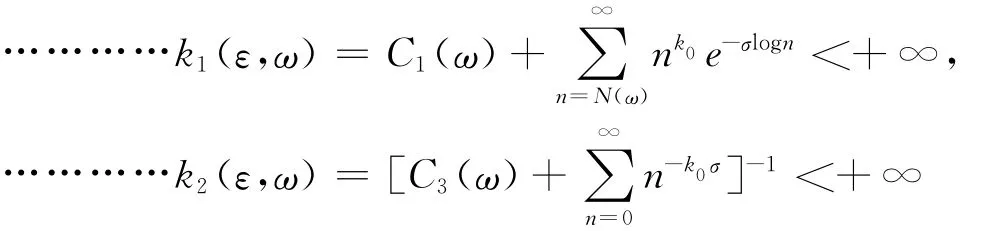
所以就有

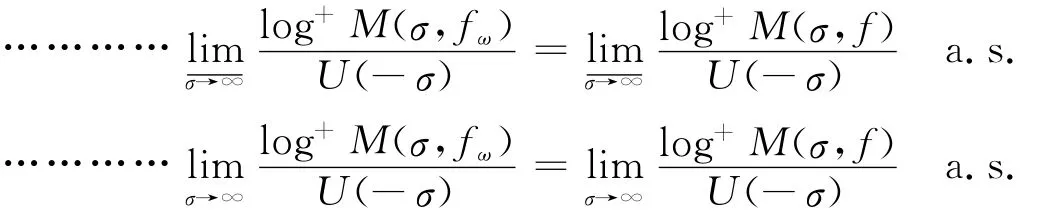
由此可见,定理2成立.

［1］刘薇.零级随机Dirichlet级数增长性［J］.纺织高校基础科学学报,2006,19(2)：122-125

［2］高宗升.零级狭里克莱级数的增长性［J］.武汉大学学报：自然科学版,1994(2)：1-8.

［3］高宗升.Dirichlet级数表示的整函数的增长性［J］.数学学报,1999.42(4)：741-748.

［4］余家荣,丁晓庆,田范基.Dirichlet级数与随机Dirichlet级数的值分布［M］.武汉：武汉大学出版社,2004.

［5］马昌秀,杨锦华,田宏根.零级Dirichlet级数在全平面上的增长性［J］.新疆师范大学学报(自然科学版),2007,26(1)13-16.

(编辑:郝秀清)

The growth of random dirichlet series of zero order

ZHANG Hai-xia
(School of Mathematics and Statistics,Xuchang University,Xuchang 461000,China)

When random variables fitfor some conditions,two theorems which concern about the growth of this random Dirichlet series of zero order in the plane are obtained.

Dirichlet series；zero order；growth

1672―6197(2013)01―0013―04

O174.52

A

2012- 10- 15

河南省教育厅自然科学基金资助项目(2011A110020)；河南省骨干教师资助项目(2011GGJS-182)；河南省社科联、河南省经团联调研资助项目(SKL-2012-2334)；许昌学院校级科研资助项目(2013096)

张海侠,女,zhx_1010@126.com