车辆随机振动稳定性分析

吕士宝,张丽,赵花妮

(兰州交通大学数理与软件工程学院,甘肃兰州730070)

车辆随机振动稳定性分析

吕士宝,张丽,赵花妮

(兰州交通大学数理与软件工程学院,甘肃兰州730070)

以1/4车辆两自由度模型为研究对象,研究了线性与非线性悬架系统车辆行驶的稳定性.在线性悬架系统中,利用虚拟激励法推导出车辆加速度功率谱密度函数表达式,借助MATLAB仿真分析了当车辆各参数在一定范围内变化时车辆行驶的平顺性.当车辆悬架刚度、阻尼等分别作为随机参数,且参数服从正态分布时,利用四阶Runge-kutta数值方法,对非线性悬架系统的动力学行为进行了数值仿真.仿真结果表明,合适的悬架参数,可以有效控制车辆的振动,应当重视车辆线性与非线性悬架参数的选取.

非线性悬架；随机振动；1/4车辆

车辆随机振动问题是交通部门经常遇到的问题.考虑到路面的高低不平,车辆内部各结构由于长期运行难免会出现摩擦、老化等现象.因此,结构参数的随机性是不可避免的.近年来,对车辆线性与非线性悬架模型的研究已有不少成果.文献［1］利用分岔图、时间历程图等,对车辆非线性悬架系统在正弦激励下发生混沌振动的激励频率进行数值仿真.文献［2］应用虚拟激励法,构造出虚拟路面激励,建立了求取系统响应量功率谱密度的一种快速方法.文献［3-4］主要分析了1/4车辆在固定参数下非线性悬架模型振动的稳定性.文献［5］将车辆刚度、阻尼等均认为是随机变量,通过蒙特卡罗随机模拟法研究了车辆在随机路面激励下的振动响应问题.目前对车辆随机振动的研究主要集中于固定参数下的研究,而对随机参数的研究还比较少见.鉴于此,本文在以上研究成果的基础上,研究了线性悬架车辆行驶的平顺性.对非线性悬架系统,将车辆刚度、阻尼等参数看作服从正态分布的随机参数,研究车辆行驶的稳定性.

1 车辆振动模型

选取文献［5］中某轻型轿车1/4车辆悬架模型为研究对象,将1/4车身质量与轮胎分别看成两个自由度,可将车辆系统简化为如图1所示的弹簧振子模型.图1中,c为车身悬架阻尼,忽略不计轮胎阻尼.m1、m2分别为1/4车身质量与轮胎质量(单位为kg),k1、k2分别为悬架刚度与轮胎刚度,x1、x2分别为车身、轮胎在垂直方向上产生的振动位移响应.

图1 1/4车辆两自由度模型

2 车辆系统振动稳定性分析

2.1 线性悬架平顺性分析

从车辆振动力学的角度出发,当悬架系统为线性系统时,利用牛顿第二定律对系统进行受力分析,建立车辆的线性振动学模型［2］如下：

将方程整理,用矩阵的形式可表示为

式中：M为质量矩阵；C为阻尼矩阵；K为悬架刚度矩阵；P为外激励向量；X为响应位移向量1,且

利用虚拟激励法,可得到各振动的响应量,将各响应量代入式(2),整理合并得

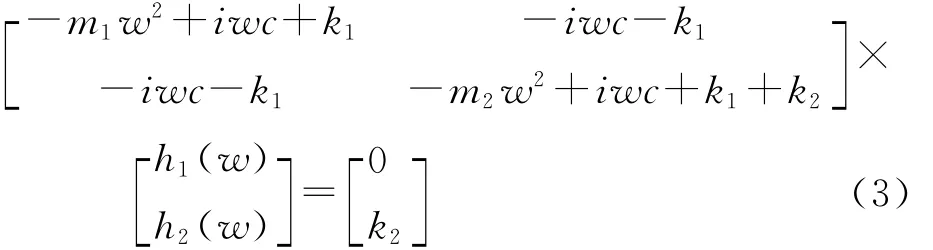
解得车身的频率响应函数为

则其对应的车身加速度功率谱密度函数为

为说明车辆各参数对响应量产生的影响,选取表1中某轻型轿车参数［5］,假定车辆以25m/s的速度匀速行驶在C级路面上(路面等级见GB7031―86),在其它各参数不变的情况下,借助MATLAB仿真软件,通过编制程序,分别考虑车身质量在0～2 000kg、悬架刚度在10 000～40 000 N/m、悬架阻尼在0～5 000 N·s/m范围内变化时,车身垂直方向加速度功率谱密度的三维图.

表1 某轻型轿车参数

图2～图4为车身质量、悬架刚度、阻尼等在一定范围内变化时的车身功率谱.车辆主要集中于低频范围振动(0～15Hz),当激励频率在1～2 Hz与10 Hz附近出现明显的两个波峰,说明车辆振幅较大,行驶的平顺性较差.此外,车辆结构参数的选取对振动会产生较大影响.当车辆以25m/s的速度匀速行驶在C级路面时,车身质量在200～300kg、刚度在10 000～20 000 N/m、阻尼在1 000～2 000 N·s/m的范围内变化,车身振动波峰最低,行驶的平顺性较好.在悬架优化设计中,应选取合适的参数,保证车辆行驶的稳定性和安全性.

图2 车身质量不确定时车身加速度功率谱

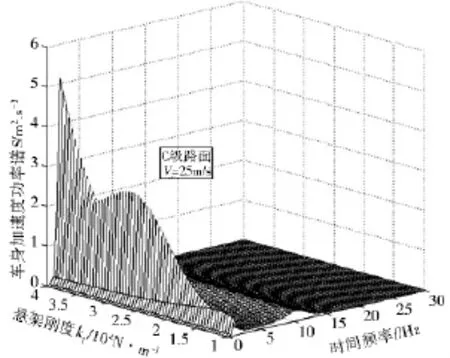
图3 悬架刚度不确定时的车身加速度功率谱

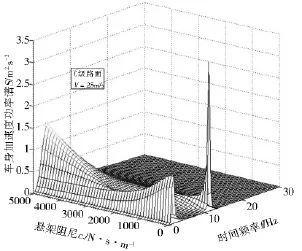
图4 悬架阻尼不确定时的车身加速度功率谱

2.2 非线性悬架系统稳定性分析

当车辆悬架弹簧为非线性刚度弹簧时,力与位移之间的关系可表示为

我们建立如下微分学方程［4］：

把车辆系统受到来自路面的随机激励近似看成一周期激励.令q=A sin(wt),ε=0.1,取A=0.5,w为外激励频率,系统的固有频率为

利用MATLAB四阶Runge―kutta数值方法,对系统进行仿真分析.

(1)悬架刚度为随机参数时对稳定性的影响

考虑当悬架刚度为随机参数时,悬架刚度系数服从正态分布,即K1～N(16 000,1 6002),悬架阻尼与质量取固定参数.在主共振下(=8)对该系统的动力学方程进行数值求解,得车身与轮胎的时间历程与相平面如图5所示.

(2)悬架阻尼为随机参数时对稳定性的影响

当车辆悬架阻尼不确定时,阻尼系数服从正态分布C～N(980,982),其它参数为固定参数,次谐波共振下(w＞=27)对该系统的动力学方程进行数值求解,得车身与轮胎时间历程与相平面如图6所示.

图5、图6分别为主共振(w≈w0=8)下刚度随机和次谐波共振(w＞3w0=27)下阻尼随机时车身与车轮胎的时间历程与相图.无论在哪种情况下,相轨迹从初始状态出发,经过短暂的震荡后,最后都集中在以原点为中心的封闭椭圆区域,表明该动力系统在悬架刚度及阻尼系数服从正态分布的情况下均为稳定的.说明车身及车轮的运动是稳定的,并未发生明显的混沌振动.

图5 主共振下刚度随机时车身与轮胎时间历程与相平面轨线

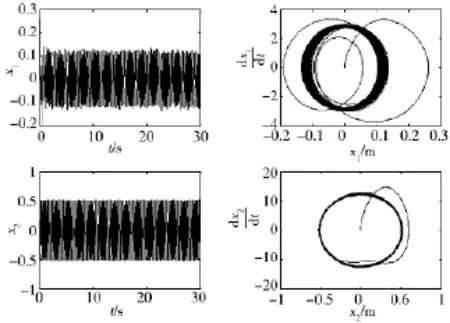
图6 次谐波共振下阻尼随机时车身与轮胎时间历程与相平面轨线

比较图5与图6可知,无论是悬架刚度为随机参数,还是阻尼为随机参数,车身振动的相平面轨线随激励频率发生较大变化,而车轮的相轨迹变化较小,表明随机参数下外激励频率对车辆动力系统影响较大.

3 结束语

本文以1/4车辆两自由度模型为研究对象,研究了线性悬架与非线性悬架车辆行驶的平顺性、稳定性.运用四阶Runge―kutta数值方法,对正弦激励条件下非线性悬架模型动力学行为的.仿真结果表明,当车辆刚度、阻尼等系数服从正态分布时,车身与轮胎的振动是稳定的,并未发生明显的混沌振动,车辆行驶的稳定性较好.

［1］梁山,郑剑,朱勤,等.非线性车辆模型混沌振动的仿真与实验研究［J］.机械强度,2012,34(1)：6-12.

［2］李杰,秦玉英,赵旗,等.用于分析车辆随机振动的一种新方法［J］.机械设计,2009,26(4)：14-17.

［3］Von Wagner U.On non-linear stochastic dynamics of quarter car models［J］.Int J.Non-Linear Mech,2004(39)：753-765.

［4］成洁.车辆悬架系统非线性振动特性研究［D］.西安：西北工业大学,2006.

［5］戴君.基于四分之一车辆模型的具有随机结构参数车辆的随机动力分析［J］.振动与冲击,2010,29(6)：211-215.

(编辑:郝秀清)

Stability analysis of the vehicle random vibration

LYU Shi-Bao,ZHANG Li,ZHAO Hua-ni
(School of Mathematics,Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)

By taking two degrees of freedom model of the 1/4 vehicles as the study object,the paper analyzes the vehicle stability in both linear and nonlinear suspension systems.In the linear suspension system,Pseudo Excitation Method is adopted to derive acceleration power spectral density function expression of the vehicle.When parameters of the vehicle are changed within a certain range,MATLAB is used to simulate the riding comfort of the vehicle.In the nonlinear suspension system,when vehicle suspension stiffness and damping are respectively taken as random parameters and meanwhile these parameters follow the normal distribution,the numerical method of Fourth-order Runge-kutta is employed to simulate the dynamic behavior of the system. The above two simulations show that appropriate parameters of the suspension can effectively control the vibration of the vehicle and that attention should be paid to the selection of the parameters of vehicle linear and nonlinear suspension.

nonlinear suspension；random vibration；1/4 vehicle

1672―6197(2013)01―0005―04

O324

A

2012- 11- 02

国家自然科学基金资助项目(11262009)；甘肃省自然科学基金资助项目(1208RJZA111)

吕士宝,男,shibao998@163.com