双参数指数分布步加试验TFR模型下修正的MLE

周伟萍,王丰效

(喀什师范学院数学系,新疆喀什844006)

双参数指数分布步加试验TFR模型下修正的MLE

周伟萍,王丰效

(喀什师范学院数学系,新疆喀什844006)

给出了双参数指数分布全样本场合下步进应力加速寿命试验TFR模型下参数的修正极大似然估计,并通过Monte-Carlo模拟证明了修正的极大似然估计要好于极大似然估计.

双参数指数分布；步加试验；TFR模型；极大似然估计

目前对步进应力加速寿命试验TFR模型的统计分析已有不少研究,具体可参阅文献［1-14］.文献［14］给出了全样本场合下双参数指数分布步进应力加速寿命试验TFR模型下参数的极大似然估计.虽然极大似然估计有良好的大样本性质,但是文献［14］中门限参数的极大似然估计往往偏大.本文就是基于这一事实,利用纠偏的思想,构造一新的统计量,给出参数的修正极大似然估计,并且把改进后估计量与文献［14］中给出的参数的MLE作模拟比较,以期使改进后估计量的相对误差有明显减小.

约定如下记号：用随机变量Y表示在一个持续应力下某产品的寿命时间,它的分布函数、密度函数、残存函数和失效函数分别用和来表示,不同应力场合下的各量,可通过添加一个下标来表示.例如,在应力下,将表示产品寿命时间的分布函数.而步进应力加速寿命试验中将用来表示产品的寿命时间,当指的是时,以上所提到的每个函数都要加一个星号.

可以得到相应的残存函数

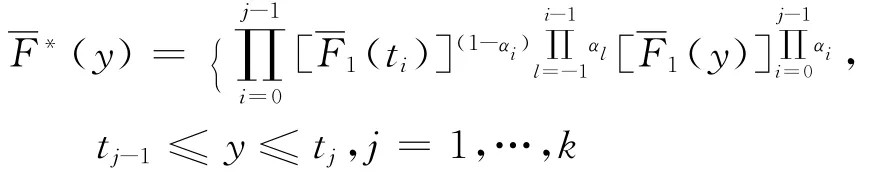
特别地,如果是考虑简单步进应力加速寿命试验场合,即将n个产品,在应力下试验做到时刻,紧接着将应力提高到,试验做到时刻,此时TFR模型的失效率函数、残存函数分别为

1 完全样本场合步进应力加速寿命试验TFR模型下参数的修正MLE

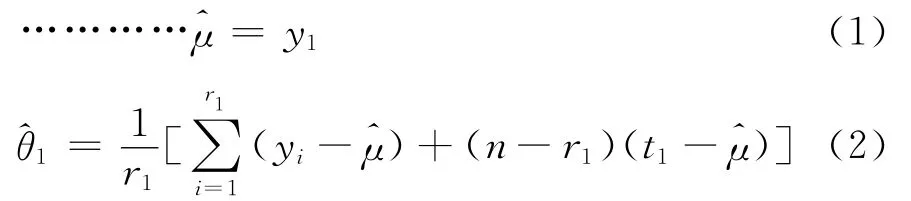
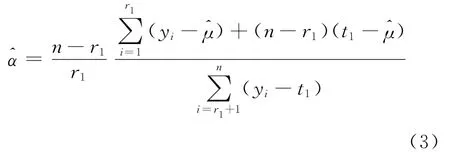
由于门限参数μ≤y＜∞,所以用ˆμ=y1来估计μ时往往会偏大.关于门限参数μ的估计的修正基于如下事实：

从而在式(1)～式(3)的基础上,我们利用纠偏的思想构造及因子α的新估计：

2 Monte-Carlo模拟实例

例1［14］取样本容量n=15,参数真值取为μ= 10,=1,α=3,另外取=5,通过Monte-Carlo模拟得到如下失效数据：10.048 0,10.068 0,10.254 0,10.258 1,10.336 0, 10.411 3,10.455 7,10.461 8,10.465 9,10.550 9, 10.556 0,10.626 7,10.631 4,11.338 2,11.662 4.

模拟比较的结果见表1(其中MEL的结果来自于文献［14］).

例2［14］取样本容量n=20,参数真值取为μ=15=5,α=2,另外取=7,通过Monte-Carlo模拟得到如下失效数据：

15.130 1 ,15.289 0,15.475 6,16.377 7, 16.588 0,17.352 7,17.449 6,17.586 8,17.612 3, 18.500 3,18.903 6,18.926 3,19.175 4,19.249 5, 19.725 1,19.872 2,20.022 2,20.997 9,23.898 7, 29.132 6.

模拟比较的结果见表2(其中MEL的结果来自于文献［14］).

表1 MMLE与MLE的模拟比较结果

表2 MMLE与MLE的模拟比较结果

从表1和表2可以看出,在全样本场合下从参数估计的相对误差来看,修正的极大似然估计(MMLE)要优于极大似然估计(MLE).

例3 为了有一个横向的比较,针对小样本、中样本和大样本这三种情况分别产生随机数.参数真值取为μ=25,θ1=5,α=10,在这样的前提下,通过Monte-Carlo方法进行数据模拟。当取n=50(小样本)时,取r1=30；当取n=200(中样本)时,取r1=100；当取n=1 000(大样本)时,取r1=800.表3中给出了MLE(文献［14］中的方法)和本文讨论的MMLE(修正极大似然估计)模拟结果.

表3 小样本、中样本和大样本的MMLE与MLE的模拟比较结果

从表3可以看出,在小样本、中样本和大样本这三种情况下,本文讨论的MMLE(修正极大似然估计)整体上要优于MLE(文献［14］中的方法),更适合研究者采用。

3 结束语

由模拟结果可知,本文给出的修正极大似然估计方法从相对误差的角度来看要优于极大似然估计,因此本文提出的修正极大似然估计方法是可行的,也是比较理想的.

［1］Bhattacharyya G K,Soejoeti Z.A tampered failure rate model for step-stress accelerated life test［J］.Communication in Statistics Theory and Methods,1993,22(9)：2 631-2 639.

［2］Madi M T.Multiple step-stress accelerated life test：the tampered failure rate model［J］.Communication in Statistics Theory and Methods,1993,22(9)：295-306.

［3］Seiji Nabeya.Coincidence of two failure rate models［J］.Communication in Statistics Theory and Methods,1993,22(3)：781-785.

［4］Rao B,Ra J.Equivalence of the tampered random variable and the tampered failure rate models in accelerated life testing for a class of life distributions having the“setting the clock back to zero property”［J］.Communication in Statistics Theory andMethods,1992,21(3)：647-664.

［5］陈迪.步进应力加速寿命试验的比例失效率模型［C］//首届中国运筹学会青年可靠性学术会议论文集——可靠性理论、方法及应用.北京：机械工业出版社,1994.62-66.

［6］Wang R H,Fei H L.Uniqueness of the maximum likelihood estimate on the Weibull distribution tampered failure rate model［J］.Communication in Statistics Theory and Methods,2003,32 (12)：2 321-2 338.

［7］Wang R H,Fei H L.Conditions for the coincidence of the TFR,TRV and CE models［J］.Statistical Papers,2004,45：393-412.

［8］王蓉华,费鹤良.TFR、TRV和CE模型序加试验下Weibull分布产品的失效分布［J］.运筹与管理,2002,11(5)：47-55.

［9］Wang R H,Fei H L.Statistical inference of weibull distribution for tampered failure rate model in progressive stress accelerated life testing［J］.Journal of Systerms Science and Complexity, 2004,17(2)：237-243.

［10］王蓉华,费鹤良.TFR模型序加试验下Weibul1分布产品寿命的统计分析［J］.运筹与管理,2004,13(2)：39-44.

［11］Xu X L,Fei H L.Approximate maximum likelihood estimate and inverse moment estimates of the parameters of the tampered failure rate model for the weibull distribution in a step-stress accelerated life test［J］.数学研究,2003,36(4),351-367.

［12］Xu X L,Fei H L.Parameter estimation of the weibull distribution tampered failure rate model under a normal stress［J］.应用概率统计,2004,20(2)：126-132.

［13］王蓉华,徐晓岭,施宏伟.Gompertz分布TFR模型多步步进应力加速寿命试验的统计分析［J］.应用概率统计,2009,25(1)：47-59.

［14］王蓉华,徐晓岭,刘文华,等.两参数指数分布产品全样本场合下步进应力加速寿命试验损伤失效率模型下的统计分析［J］.运筹与管理,2007,16(3)：74-77.

(编辑:郝秀清)

The modified MLE of parameters of two-parameter exponential distribution based on TFR model under step-stress accelerated life testing

ZHOU Wei-ping,WANG Feng-xiao
(Department of Mathematics,Kashi Teachers College,Kashi 844006,China)

We obtain the modified maximum likelihood estimator of parameters of two-parameter exponential distribution with full sample size based on tampered failure rate model under stepstress accelerated life testing,and show that the modified maximum likelihood estimation is better than the maximum likelihood estimation through the Monte-Carlo simulation.

two-parameter exponential distribution；step-stress accelerated life testing；tampered failure rate model；maximum likelihood estimator

1672―6197(2013)01―0030―04

O213.2

A

2012- 12- 26

喀什师范学院一般课题((11)2389)

周伟萍,女,470988895@qq.com