天津市设计暴雨方法比较及公式修正
2013-06-24黄津辉向文艳范泽华
黄津辉,向文艳,户 超,范泽华,郭 军
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;
2. 河海大学水利水电学院,南京 210098;3. 天津市气象中心,天津 300072)
天津市设计暴雨方法比较及公式修正
黄津辉1,向文艳1,户 超2,范泽华1,郭 军3
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;
2. 河海大学水利水电学院,南京 210098;3. 天津市气象中心,天津 300072)
设计暴雨是防洪设施建设的安全标准之一,由于气候改变,水文循环过程随之改变,降雨强度及规律也相应发生改变,因此有必要对设计暴雨进行进一步研究.以天津市为研究对象,采用52年P-Ⅲ型的降雨资料作为样本;采用年最大值法、年多个样法进行选样,采用耿贝尔分布、广义极值分布、指数分布和P-Ⅲ型分布对设计暴雨进行理论频率分析,以回归分析中的决定系数作为评价指标.通过频率适线分析得出暴雨强度-历时-重现期关系曲线,并采用高斯-牛顿迭代法对暴雨强度公式进行求解,以绝对标准差及相对标准差作为暴雨强度公式评价指标.结果表明P-Ⅲ型曲线更为适用,而目前使用的设计暴雨强度小于根据52年降雨资料得出的设计暴雨强度.因此,随着数据的积累对设计暴雨进行修正是非常必要的.
设计暴雨;城市内涝;理论频率分析;I-D-T曲线
气候变化造成水文循环的改变,使水文极值事件的强度和频次改变,破坏了原有的水文统计规律.在进行水库、大坝以及城市蓄水和排涝设施等设计时,目前使用的设计暴雨由于研究时间早,利用的统计数据有限,已经不能满足气候变化条件下对工程安全及人民生活财产安全的要求.近几年,中国北京、上海、广州、天津等大城市相继遭到暴雨袭击,2012年尤为严重.2012年7月21日,北京发生自1951年以来有完整气象记录的最大降雨,平均日降雨量为170,mm,北京最大降雨点房山区河北镇,降雨量达到521,mm,接近北京平均年降雨量;该次暴雨造成190万人受灾,77人死亡,经济损失116.4亿元.而天津在7月21日至22日平均降雨为98.6,mm,北部宝坻区大白庄降雨量达到294.7,mm,在7月25日至7月26日降雨量达到195.0,mm,造成巨大经济损失.在多雨的南方地区,暴雨同样造成严重的洪涝灾害.国外很多大城市也遭受大暴雨事件袭击,导致城市内涝,造成重大损失,设计暴雨的准确性直接关系到城市雨洪设施设计等的准确性,因此,对设计暴雨进行修改及更新至关重要,国内外专家学者有许多相关方面的研究[1-4].
依据《室外排水设计规范》(GB50014—2006)[5],中国暴雨选样采用年多个样法选样.年多个样法选样统计工作繁琐,工作量大,这一方法相对适用于早期数据积累不完善、样本年偏少的情况.年最大值法选样操作简单省时,但部分丰水年排序第2、第3的暴雨数值可能会被遗漏,造成重现期偏小的问题,尤其是数据少于30年的情况下尤为突出,因为对百年一遇的暴雨,要有30年的数据,预测才可能比较精确.对此,在以往的研究中,由于数据积累的问题,有些学者提出使用年超大值法进行选样,有学者提出采用改进的年最大值法,国外早年多采用超定量法选样,后来由于数据量增大,广泛改用年最大值法选样;随着我国各地气象水文数据不断积累完善,资料年份长,许多地区的资料都已达到20~30年,个别地区已有60~70年[6-7].
暴雨频率分布线型的选取是影响设计暴雨精确度的十分重要的因素,世界上许多国家都制定了当地的设计暴雨规范或标准,统一采用某一种理论概率分布线型;也有一些国家没有制定统一的规范或标准,通过其经验或统计检验比较,选择出区域最适合的分布线型.
中国目前在设计暴雨的研究中使用的极值分布频率曲线主要是P-Ⅲ型曲线.根据我国《室外排水设计规范》(GB50014—2006)建议,为达到高模拟精度,宜选用P-Ⅲ型频率分布曲线.但是部分学者认为P-Ⅲ型频率分布曲线是三参数的,拟合较困难,不如耿贝尔分布及指数分布计算简易[6].为此,笔者以天津市为例,对设计暴雨的选样方法及理论频率分析方法进行了探讨及对比,并对天津市的设计暴雨强度公式进行了修正.
1 研究方法
1.1 数据和选样方法
在水文统计学中,暴雨的选样方法主要包括年最大值法和非年最大值法,其中非年最大值法又包括年超大值、超定量法和年多个样法.年最大值法是以年份为序,每年选取一个最大值,N年共选取N个最大值.年超大值法是每年挑选几个最大值,不同历时的样本按大小顺序排序,选取最大的N个数值,平均每年选用一组.超定量法是根据当地的规范,选取标准暴雨值以上的所有暴雨数据.年多个样法是从每年挑选6~8组最大雨样,不论年次,各历时按降序排列,选择资料年数3~4倍数量的最大值.从以上选样方法看来,非年最大值法弥补了年最大值法的部分缺陷,不会遗漏丰水年排序第2或第3的暴雨值,最后的计算结果更加准确.本文根据天津市的实测资料,采用年最大值法和年多个样法选样[5-7],运用不同的频率分布曲线进行适线分析,通过对不同选样方法及不同频率分析方法的对比分析,确定更适合的暴雨强度公式.
天津市位于海河流域,东经116°43'至118°04'、北纬38°34'至40°15' 之间,其流域地理位置如图1所示.

图1 天津市在海河流域地理位置Fig.1 Location of Tianjin in Hai River basin
天津市气象局提供了经过校核的降雨资料,年限为1955—2009年,其中2001—2003年资料缺失,总共52年暴雨资料,样本容量大,满足《室外排水设计规范》(GB50014—2006)[5]的要求(资料条件较好时,资料年数≥20年),降雨序列包含的暴雨极值代表性全面,能够反映降雨过程.降雨资料台站为中国地面气候台站,天津市塘沽站,台站区站号54623,经度为117°43′,纬度为39°03′,具有代表性,站点位置如图1所示三角点.对于年最大值法选样,每个历时选取52个数据;对于年多个样法选样,每年各个历时选取6个最大值,再从中选取资料年限4倍的数据,每个历时选择208(52×4)个数据.
1.2 理论频率分布模型
本文针对年最大值法采用耿贝尔分布和广义极值分布,针对年多个样法采用指数分布和P-Ⅲ型分布进行适线分析[8-11],对结果进行了较为系统的比较与讨论.由于这些分布模型在很多论文及书籍中已有详细阐述,这里只给出各暴雨频率分布模型的概率函数,见表1.

表1 暴雨频率分布模型概率函数Tab.1 Equations of theoretical frequency distributions
适线分析评价指标采用决定系数R2[12].决定系数是指回归平方和在总平方和中所占的比率.变量间共变程度的指标,等于回归平方和与总平方和之比,亦即相关系数的平方.对于一元线性回归分析和多元线性回归分析,决定系数以R2表示.决定系数可作为曲线(或直线)拟合样本数据程度好坏的指标.决定系数越大说明回归平方和对总体平方和的贡献越大,回归效果越好.决定系数R2的表达式为
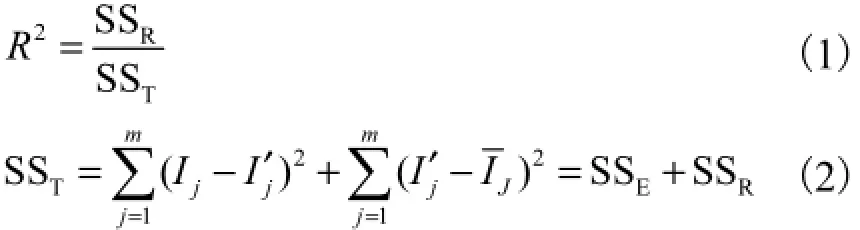
式中:SST为总的变差平方和;SSE为剩余平方和;SSR为回归平方和;jI为第j个实测暴雨强度值;为第j个拟合值或回归值;为平均暴雨强度;m表示数据总个数.
1.3 暴雨强度公式及参数求解
暴雨强度公式包括单一重现期公式和统一公式.单一重现期公式是对一个重现期编制的,只对m个(D,I)经验点进行曲线拟合,而各重现期统一公式是对所有重现期编制的,要对m×n个经验点同时进行拟合,所以前者比后者拟合较好,且编制单一重现期公式要比编制各重现期统一公式简单省事.统一公式,可以为绘制国家或某大区域的暴雨强度公式中各参数的等值线服务,可以更好地了解全国或各大区域的降雨分布规律.
根据《给水排水设计手册》[13],单一重现期计算式为

式中:I为暴雨强度,mm/min;D为降雨历时,min;A、B和n为待求参数,无量纲.求A、B和n的过程相当于曲线拟合,可以通过求解超定非线性方程组而求得.
暴雨强度统一公式采用张子贤[14]提出的公式,即

式中:T为重现期,a;A1、C、b和N为待求参数,无量纲.对于参数求解,应用最小二乘法.
暴雨强度公式参数求解的优劣需要用一定标准来衡量.《室外排水设计规范》(GB50014—2006)[5]明确规定:在比较所选择的暴雨强度公式的精度时,以绝对标准差最小为优来判别其优劣,也可以辅以相对标准差.本文选用这2种评价标准进行计算比较.绝对标准差用σ表示,相对标准差用ω表示,表达式分别为

2 结果及讨论
2.1 选样结果
对于年最大值选样方法采用的降雨历时为15个,即5,min、10,min、15,min、20,min、30,min、45,min、60,min、90,min、120,min、180,min、240,min、360,min、540,min、720,min、1,440,min.对于年多个样法选样采用的降雨历时为10个,即5,min、10,min、15,min、20,min、30,min、45,min、60,min、90,min、120,min、180,min.各历时在所有年份的最大值、最小值及多年平均值列于表2.

表2 各历时最大暴雨统计Tab.2 Maximum storm for every duration mm
2.2 理论频率曲线适线成果
对年最大值法得到的数据样本,采用耿贝尔分布及广义极值分布进行适线分析;对年多个样法得到的数据样本,采用指数分布及P-Ⅲ型分布进行适线分析.采用决定系数评价适线成果的好坏.下面给出各频率曲线适线图的决定系数,结果见表3.

表3 决定系数R2对比Tab.3 Comparison of determination coefficient R2
由表3可以看出,在年最大值法选样的15个历时中,60,min、90,min和120,min历时耿贝尔分布的决定系数大于广义极值分布的决定系数,因此对于这3个历时耿贝尔分布为优;540,min及720,min 2个历时2者决定系数相等;其他10个历时广义极值分布的决定系数均大于耿贝尔分布的决定系数,广义极值分布为优,对于67%的历时,广义极值分布为优.在大多数条件下,广义极值分布对数据拟合优于耿贝尔分布,拟合精度更高,因此宜优先考虑广义极值分布.
在年多个样法选样的10个历时中,均为P-Ⅲ型分布的决定系数大于指数分布的决定系数,表明在相同的历时条件下,P-Ⅲ型分布对数据拟合优于指数分布,拟合的精度更高,因此在同等条件下,宜优先考虑P-Ⅲ型分布.
对于4种理论频率分布的决定系数进行比较,可以看出其值均在0.99以上,拟合度均较好.从表3中可以看出10个历时中最大值对应的理论频率分布均为P-Ⅲ型分布.验证了P-Ⅲ型分布在天津市暴雨强度分析中的适用性,及年多个样法的优越性.
根据《室外排水设计规范》(GB50014—2006)[5]规定:取样方法宜采用年多个样法.如果直接采用年最大值法进行城市暴雨强度的计算会与现在的状况不协调,目前直接采用年最大值法还有一定困难,在设计上仍旧不能被接受,但是年最大值法相对年多个样法,更为简单,对于不缺少自动雨量记录的地区,年最大值不失为一种好方法.
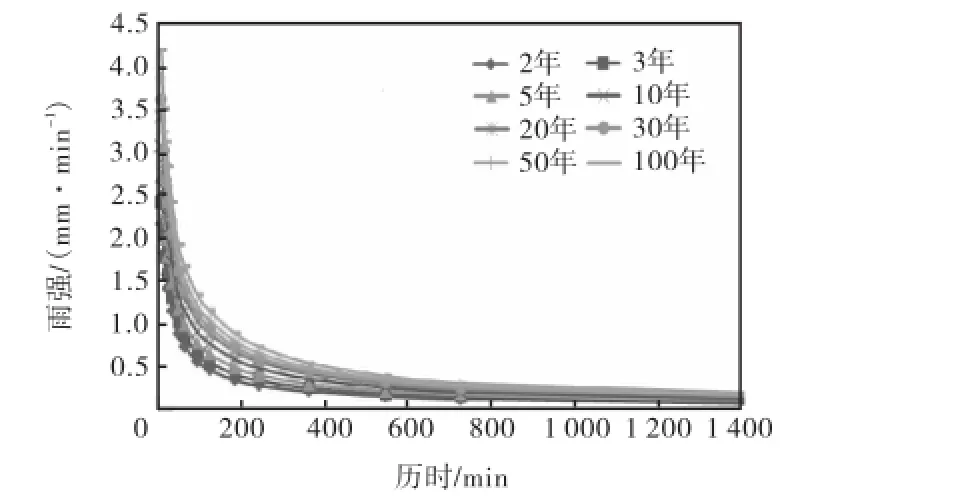
图2 耿贝尔分布拟合的I-D-T关系曲线Fig.2 I-D-T curves for Gumbel distribution
2.3 暴雨强度-历时-重现期(I-D-T)关系曲线
根据不同频率理论分布的适线分析成果得出不同重现期下不同历时对应的暴雨强度(简称雨强),并绘制出暴雨强度-历时-重现期(I-D-T)的关系曲线,重现期为0.25~100年,如图2~图5所示.
由图2~图5中可知,4种理论频率分析对应的I-D-T曲线变化趋势较为一致,但仍有区分.同一重现期,暴雨强度随着降雨历时的延长而减小,当降雨历时超过120,min以后,曲线变得较为平缓;同一降雨历时的暴雨强度,随着重现期的增加而增加;大重现期对应的曲线总是位于小重现期对应曲线的上方.由于耿贝尔分布和广义极值分布的降雨历时比较长,因此图中I-D-T曲线比较紧凑.

图3 广义极值分布拟合的I-D-T关系曲线Fig.3 I-D-T curves for generalized extreme value distribution

图4 指数分布拟合的I-D-T关系曲线Fig.4 I-D-T curves for exponential distribution

图5 P-Ⅲ型分布拟合的I-D-T关系曲线Fig.5 I-D-T curves for P-Ⅲ distribution
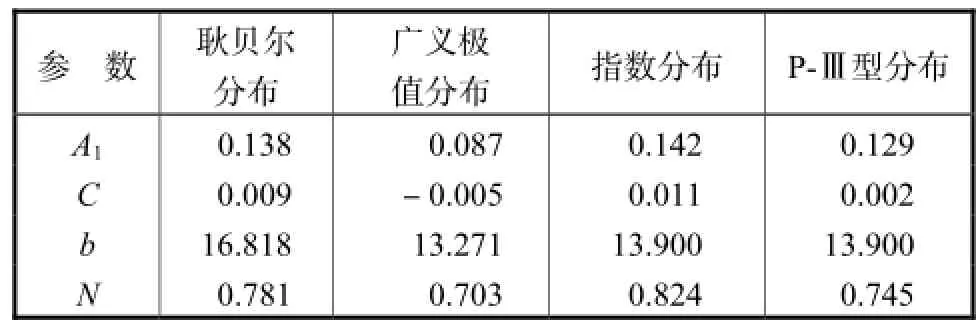
表4 暴雨强度公式参数值Tab.4 Parameters of storm intensity formula
2.4 暴雨强度公式
根据式(3)提供的单一重现期暴雨强度公式的求解方法,分别根据耿贝尔分布、广义极值分布、指数分布和P-Ⅲ型分布的I-D-T关系表中的数据进行拟合,求解单一重现期暴雨强度公式,得到参数A、B、n.根据式(4),利用高斯-牛顿迭代法对统一暴雨强度公式进行求解,得到参数A1、C、b和N,见表4.
根据式(5)和式(6)分别计算4种理论曲线所得单一暴雨强度公式对应的绝对标准差及相对标准差,结果见表5.
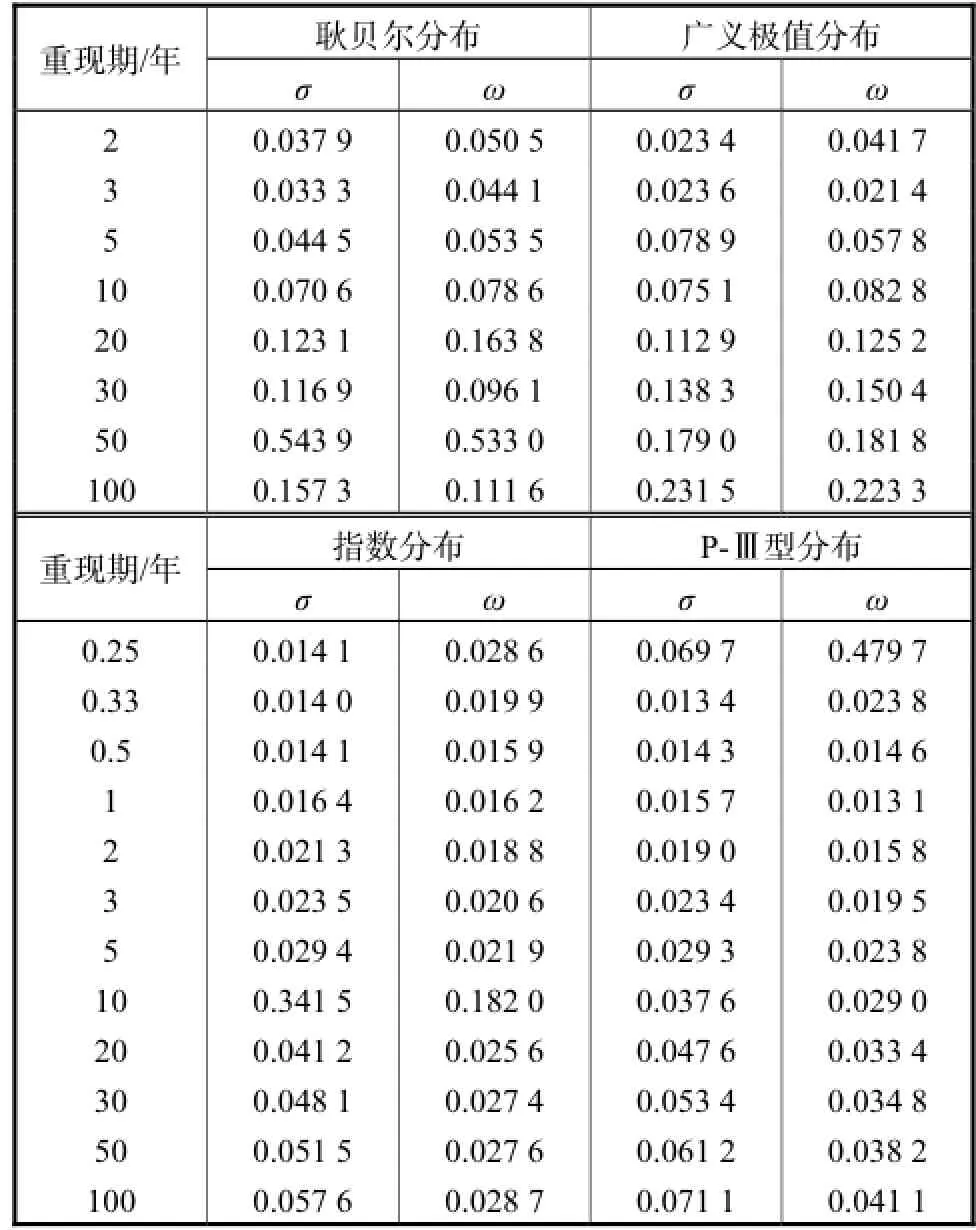
表5 暴雨强度公式评价指标对比Tab.5 Comparison of evaluation index for storm intensity formula
按照标准差最小为优原则,从表5中数据可以看出在所有重现期中,绝对标准差最小值和相对标准差最小值均出现在年多个样法选样.而对于年多个样法选样的12个重现期中,绝对标准差在重现期为0.25、0.5、20、30、50和100年时最小值对应的分布为指数分布,在重现期为0.33、1、2、3、5和10年时最小值对应的分布为P-Ⅲ型分布,指数分布和P-Ⅲ型分布各占50%,且P-Ⅲ型分布相对于小重现期较优,而指数分布相对于大重现期较优.在重现期为0.25年时,指数分布优势明显,在重现期为10年时,P-Ⅲ型分布优势明显,其他10个历时中,两者差别均在0.02,mm/min以下,差距不大.
对于相对标准差,重现期为0.25、0.33、5、20、30、50和100年时,最小值对应的分布为指数分布,重现期为0.5、1、2、3和10年时,最小值对应的分布为P-Ⅲ型分布,指数分布为优占58%,P-Ⅲ型分布为优占42%,同样说明P-Ⅲ型分布相对于小重现期较优,指数分布相对于大重现期较优.重现期为0.25年时,指数分布优势明显,在重现期为10年时,P-Ⅲ型分布优势明显,在其他10个历时,两者差值均在2%以下,差别不大.从以上分析可以看出,绝对标准差及相对标准差2个评价指标的评价结果基本一致.
因此,在重现期为0.25年时,建议使用指数分布,在重现期为10年时,建议用P-Ⅲ型分布,其他10个历时用指数分布和P-Ⅲ型分布都比较合理.根据《室外排水设计规范》(GB50014—2006),计算重现期在0.25~10年时,在一般强度的地方,平均绝对标准差不宜大于0.05,mm/min,指数分布平均绝对标准差为0.056,mm/min,大于标准要求;P-Ⅲ型分布平均绝对标准差为0.037,mm/min,小于标准要求,说明P-Ⅲ型分布更适宜.这个结果也充分说明了年多个样法及P-Ⅲ型分布在天津市设计暴雨的适用性.虽然年多个样法选样复杂,计算耗时,但是如今计算机技术发达,通过编程很容易实现快速准确的计算,因此仍然建议使用年多个样法选样.
天津现行的城市暴雨强度公式可在《给水排水设计手册》[13]第5册《城镇排水》中查询,即

式中:I为暴雨强度;T为重现期;D为历时.式(7)是同济大学根据1939—1953年共15年的资料,通过解析法计算得出.
图6为4种理论曲线分布单一暴雨强度公式对应的重现期为2年的暴雨拟合的强度-历时(I-T)关系曲线对比.从图6中可以看出,年多个样法拟合的暴雨强度曲线数值均比年最大值法拟合的暴雨强度曲线数值大,而年多个样法对应的2组曲线几乎重合,年最大值法对应的2组曲线也相差不大,说明年多个样法模拟优于年最大值法.这主要是因为年最大值法选样会遗漏一些在年内排位第2或第3的暴雨,使得小重现期部分的暴雨强度明显偏小.
图7为指数分布和P-Ⅲ型分布的统一暴雨强度公式在2年重现期的新旧公式的暴雨强度-历时曲线对比.由图7可以看出,指数分布及P-Ⅲ型分布新编公式的设计暴雨强度值均比现行设计暴雨值大.可能原因一是近些年来气候变化比较大,对降雨产生了影响,使得降雨强度普遍增大;二是当年推导暴雨降雨公式时,用到的降雨资料较少,推导的暴雨强度公式精度较差.这也表明重新修订暴雨强度公式的必要性.
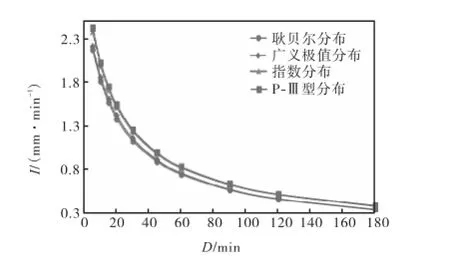
图6 重现期为2年I-D曲线对比Fig.6 Comparison of I-D curve in 2-year return period

图7 重现期为2年设计降雨强度新编公式与旧公式的对比Fig.7 Comparison of design storm intensity in 2-year return period between new and old formula
3 结 论
(1) 在年最大值法选样计算结果中广义极值分布优于耿贝尔分布;在年多个样法选样计算结果中P-Ⅲ型分布优于指数分布;且年多个样法优于年最大值法.在总体对比上,P-Ⅲ型分布的决定系数优于其他3种理论分布,验证了P-Ⅲ型分布在天津市暴雨强度分析上的适用性.虽然P-Ⅲ型分布是三参数模型,模拟计算起来比较繁琐,但是其拟合结果最佳,现今计算机技术发达,因此应用P-Ⅲ型分布更合适.
(2) 通过对比不同的I-D-T曲线,可以看出,同一重现期,暴雨强度随降雨历时的延长而减小,同一降雨历时的平均暴雨强度随重现期的增加而增加.当降雨历时超过120,min后,曲线变得较为平缓,说明暴雨历时超过2,h后的降雨强度小且变化不大.
(3) 比较分析单一重现期公式的评价指标σ及ω,可以看出年多个样法选样所得出的暴雨强度公式优于年最大值法.对于12个重现期,当重现期为0.25年时,指数分布显著优于P-Ⅲ型分布,重现期为10年时,P-Ⅲ型分布显著优于指数分布.其他10个重现期,指数分布与P-Ⅲ型分布相差不多,但σ的平均值,P-Ⅲ型分布小于0.05,mm/min,指数分布的大于0.05,mm/min,P-Ⅲ型分布略优,因此可以根据具体的精度要求进行方法的选择.单一重现期暴雨强度公式和统一公式相比,精度更高,而且便于拟合.建议对于精度要求较高的地区或重点重要的地区,可以考虑在设计时采用单一重现期公式来代替统一公式,以便更好地为区域排水服务.
(4) 以天津市降雨为例,比较研究了现行的设计暴雨公式与数据增加后推求的设计暴雨,结果表明新推求的设计暴雨大于现行的设计暴雨强度,且差异较大,建议在气象、市政、排水及水务等各部门的共同参与下,对设计暴雨进行深入的研究,并在此基础上,对现行设计暴雨进行更新.
[1] Marks M,Wuebbles D J,Liang Xinzhong. Diagnostic analysis of future climate scenarios applied to urban flooding in the Chicago metropolitan area[J]. Climatic Change,2012,111(3/4):879-902.
[2] Fowler H J. New estimates of future changes in extreme rainfall across the UK using regional climate model integrations(1):Assessment of control climate[J]. Journal of Hydrology,2005,300(1/2/3/4):212-233.
[3] Henrik Madsen. Update of regional intensity-durationfrequency curves in Denmark:Tendency towards increased storm intensities[J]. Atmospheric Research,2009,92(3):343-349.
[4] 上海市政工程设计研究总院.GB50014—2006 室外排水设计规范[S]. 北京:中国计划出版社,2006.
Shanghai Municipal Engineering Design General Institute.GB50014—2006 Code for Design of Outdoor Wastewater Engineering [S]. Beijing:China Planning Press,2006(in Chinese).
[5] 任伯帜. 采用年超大值法进行暴雨资料选样[J]. 中国给水排水,2003,19(5):79-81.
Ren Bozhi. A sampling on precipitation data by years super value method [J]. Urban Water Supply and Drainage,2003,19(5):79-81(in Chinese).
[6] Onof C,Townend J. Comparison of two hourly to 5-min rainfall disaggregators[J]. Atmospheric Research,2005,77(1/2/3/4):176-187.
[7] Palynchuk B A,Guo Yiping. A probabilistic description of rain storms incorporating peak intensities[J]. Journal of Hydrology,2011,409(1/2):71-80.
[8] Aart Overeem. Rainfall depth-duration-frequency curves and their uncertainties[J]. Journal of Hydrology,2008,348(1/2):124-134.
[9] Loukas A. Rainfall-frequency mapping for Greece[J]. Phys Chemi Earth(B),2001,26(9):669-674.
[10] Koutrouvelis I A. A comparison of moment-based methods of estimation for the Log Pearson type 3 distribution[J]. Journal of Hydrology,2000,234(1/2):71-81.
[11] Griffis V W. Log-Pearson type 3 distribution and its application in flood frequency analysis(Ⅱ):Parameter estimation methods[J]. Journal of Hydrologic Engineering,2007,12(5):492-500.
[12] Vu M T. SWAT use of gridded observations for simulating runoff—A Vietnam river basin study[J]. Hydrology and Earth System Sciences,2011,8(6):10679-10705.
[13] 北京市市政工程设计研究总院. 给水排水设计手册[M]. 北京:中国建筑工业出版社,1986.
Beijing Municipal Engineering Design Research Institute. Water Supply and Drainage Design Manual[M]. Beijing:China Architecture and Building Press,1986 (in Chinese).
[14] 张子贤. 用高斯-牛顿法确定暴雨公式参数[J]. 河海大学学报,1995,23(5):106-111.
Zhang Zixian. Application of Gauss-Netwon method to determination of parameters for storm formula[J]. Journal of Hohai University,1995,23(5):106-111(in Chinese).
Comparison of Design Storm Method and Formula Revision for Tianjin City
Huang Jinhui1,Xiang Wenyan1,Hu Chao2,Fan Zehua1,Guo Jun3
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2. College of Water Conservancy and Hydropower,Hohai University,Nanjing 210098,China;3. Tianjin Meteorology Center,Tianjin 300072,China)
Design storm is one of the most critical criteria for the design of retention or detention facilities and drainage systems,and can directly affect their safety. Due to the change in hydrologic cycle caused by global climate change,there is also a change in precipitation pattern and intensity,therefore,further study on design storm is necessary. In this paper the design storm for Tianjin City was studied by using the precipitation data collected within 52 years. Two sampling methods and four theoretical frequency distributions were employed for frequency analysis,including annual maximum method and annual multisampling method,Gumbel distribution,generalized extreme value distribution,exponential distribution and P-Ⅲ distribution.The coefficient of determination was utilized to assess the goodness of fit of those theoretical frequency distributions. Through the frequency analysis,the intensityduration-time curve was obtained. Gauss-Newton method was employed to acquire the design storm formula,the absolute standard deviation and relative standard deviation was utilized to assess the goodness of fit of design storm. The conclusion is that P-Ⅲ distribution is most appropriate in Tianjin and that the current design storm is lower than that derived from the 52 year's data. Therefore,it is necessary to study and revise the design storm with the accumulation of data.
design storm;urban flooding;theoretical frequency analysis;I-D-T curve
TV122.1
A
0493-2137(2013)04-0354-07
DOI 10.11784/tdxb20130411
2012-11-26;
2013-01-16.
教育部新世纪优秀人才支持计划资助项目(NCET-09-0586);国家气象局气象关键技术集成与应用面上项目(CMAGJ2011M05).
黄津辉(1969— ),女,博士,研究员,huangj@tju.edu.cn.
向文艳,xiangwenyanlove@163.com.
