穿江输油管道抗浮稳定最小埋深分析
2013-06-24汪彭生
戚 蓝,汪彭生,韩 东,王 伟
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
穿江输油管道抗浮稳定最小埋深分析
戚 蓝,汪彭生,韩 东,王 伟
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
穿江管道的最小埋深受到多方面因素的影响,如何确定最小埋深是穿江管道埋深设计中必须重视的关键问题.针对最小埋深传统算法的不足,提出了基于有限元的优化算法.该优化算法可综合考虑上覆土层厚度、河道行洪冲刷、地震荷载等因素的影响,得到的管道最小埋深更加符合工程实际情况.结合某实际的穿江管道工程,进行了2种计算方法的对比,分析了有限元优化算法的优越性.
有限元优化算法;最小埋深;穿江管道;抗浮稳定
输油管道布置难免要与江河交叉.综合考虑经济、美观等因素,常选择从河底穿越.输油管道直径都较大,在水中受到的浮力也较大.穿江管道穿越饱和土层,若管道的埋深不够,抗浮能力不足,上浮力超过管道上方覆土重量、管道自重及管道中油重之和时,管道将上浮和变形,可能产生透水裂缝,影响管道的施工及运行安全.因此,为满足抗浮稳定的要求,管道有一个最小埋深的问题.管道埋深必须大于最小埋深,但是,埋深太大,又会增加建设成本.这个问题对于河道较宽、河道水流冲刷较严重的地段,尤为突出.选择合理、经济的最小埋深以保证管道的稳定和结构安全.
工程中通常采用工程类比,用经验公式估算最小埋深.同时通过简单分析单位长度管道受力情况,使其受到的浮力大小等于管道排开的同体积的水重,用物理学公式进行校核,综合确立最小埋深[1-4].传统使用的工程类比法有权函数法、位移收敛法等[5-6],这些经验方法在部分工程得到了应用,但由于穿江管道的工程地质各异,外力荷载复杂,不同工况条件下的承载力与不同洪水水位下土壤材料属性等均有变化,上述传统算法仅考虑了管道及其上覆土的自重与所受浮力,据此算出的最小埋深与实际情况会有出入.
传统算法未考虑管道上覆土体厚度引起的抗摩阻力,未考虑施工及运行中河道冲刷、土层特性变化等因素的影响,计算得到的最小上覆土层厚度(即管道最小埋深)与实际需要可能有差距.对于这些影响因素,目前还没有成熟的理论方法综合考虑用来确立最小埋深.现行的相关规范,对于抗浮的设计等也没有提出明确的算法.因此,如何更合理地计算和确定大孔径穿江输油管道的最小埋深,仍是一个值得研究的问题.
笔者结合某拟建的穿江输油管道工程,采用有限元法进行数值模拟,在常规荷载组合的基础上,综合考虑上覆土层厚度、行洪冲刷深度、地震荷载和河道边界等因素的影响,通过优化计算,确定管道抗浮稳定的最小埋深.该研究结果为工程的抗浮设计提供了参考.
1 工程概况
1.1 穿江管道工程
某工程输油管道全长约2.0,km,途经某大河.与大河交叉处河道宽度约55,m,大河高水位时断面平均流速约1.45,m/s,河道冲刷明显.考虑到管道架空方式会与规划立交桥冲突,故设计管道在大河下方穿越.管道采用非开挖圆形断面顶管方式,顶管内径3.5,m,壁厚320,mm,管道容重24.5,kN/m3.管道穿越河道埋深不仅关系到稳定和结构安全,以及施工的难度,还关系管道上覆土层厚度和工作井深度对工程的影响.因此,合理确定该工程管道的最小埋深具有重要的意义.
根据设计资料与地质勘测资料,穿江管道工程土壤可分为3类:粉土、粉质黏土和黏土.以河底平面最低处为零基准面,基准面以下3,m为粉质黏土,以下3,m至7,m处为黏土,黏土之下为粉土.土层性质如表1所示.土的材料模型采用摩尔-库伦模型.
1.2 河道冲刷深度的计算
大部分的河流,河道在长期的运行过程仍会产生冲刷.管道工程穿越河道时,将对河道有不同程度的扰动,可能导致水流对河床的冲刷作用增强.对此,可考虑采用相关规范来计算河床的冲刷深度.
采用《公路工程水文勘测设计规范》[7]中的一般冲刷计算公式,可以计算河床最大冲刷深度,即

式中:hp为河床一般冲刷后最大水深,m;A为单宽流量集中系数,A=1.0~1.2;Bt为河槽部分过水净宽,m;hmt为河槽最大水深,m;ht为河槽平均水深,m;Qt为布置建筑物后河槽部分通过的流量,m3/s;IL为冲刷范围内黏性土样的液性指数,本例可取0.52.
根据本工程设计资料中河岸周边的水文地质条件与行洪流量可算得河道的最大冲刷深度.当河道特征水位为防洪警戒水位4.5,m时,算得最大冲刷深度为0.83,m;当河道水位为常水位2.8,m时,算得最大冲刷深度0.69,m;当河道无水时,无冲刷.
2 管道最小埋深的传统算法
传统算法计算穿江管道抗浮最小埋深,其原理为对比管道所受水浮力与管道、上覆土体的自重大小.即截取管道中一个单元,分析管道浮力与各部分重量总和的平衡来估计所需要的最小上覆土层厚度(即最小埋深)[8-10].计算示意见图1,具体计算方法如下.
单位长度管片上覆土柱有效重量为

单位长度管道自重为

单位长度管道所受浮力为

式中:R为管片外径;r为管片内径;cγ为管片容重,可取24.5,kN/m3;aγ为土体饱和容重;wγ为水的容重;d为上覆土层厚度.
由力的平衡可知,隧道抗浮安全稳定系数(K)为

式中K≥1.2.
对于本工程,由上述公式算得管道最小埋深d为3.36,m.

图1 管道最小覆土厚度计算示意Fig.1 Calculation sketch of the minimum thickness of overburden layers
3 管道最小埋深的有限元优化算法
考虑管道上覆土层厚度、河道冲刷的影响,采用大型通用ANSYS有限元分析软件进行最小上覆土层厚度的计算.通过参数化设计语言(APDL)编制程序,实现穿江管道最小埋深的优化计算.
3.1 有限元优化算法原理
有限元优化算法以管道抗浮最小埋深为目标函数,考虑诸如上覆土层厚度、行洪冲刷、地震荷载等对工程影响较大的因素.以全部向下的力如水重、土体重、管道重、油重、土的摩擦力和全部向上的力如上浮力等荷载,以冲刷、土层特性变化等作为优化变量.优化计算模型要同时满足管道结构本身稳定、变形和应力的形态约束条件,边界的几何约束条件,以及防止管道周边土体剪切破坏的约束条件.对于管道埋深的优化分析,其优化算法的数学表达式为
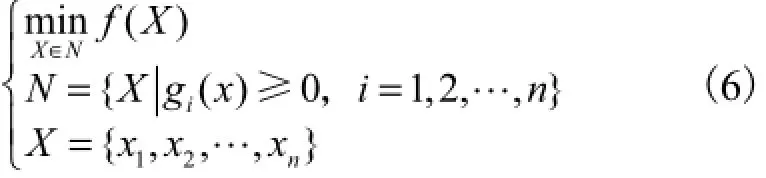
式中:X为迭代的埋深值;gi(x)为约束条件,分别为几何约束、形态约束和性状约束等;xn为优化变量,分别为荷载、冲刷深度和土层特性等.
考虑各种可能荷载的组合,选择控制荷载工况求得最小埋深,其他工况进行计算复核.有限元优化算法示意如图2所示.

图2 有限元优化算法示意Fig.2 Schematic diagram of finite element optimization method
3.2 计算流程
通过参数化设计语言(APDL)编制程序流程,在ANSYS中实现分析、评估、修正的循环,直到满足所有设计要求和约束条件,迭代求得最小抗浮埋深.程序流程如图3所示.

图3 ANSYS程序流程Fig.3 Flow chart of ANSYS program
在模型优化分析中利用了ANSYS本身的生死单元功能,单元的生死是通过修改单元刚度的方式实现的.当单元死掉时,其应力应变也被设置为零,当单元被重新激活时,它的刚度、质量与荷载等参数被返回到真实状态.可以利用这一功能模拟管道的埋深,解决有限元计算中的重复建模问题.
3.3 模型建立
按照设计需求,分别以0.50,m、0.20,m和0.05,m的精度进行网格划分,模型荷载及离散如图4所示.
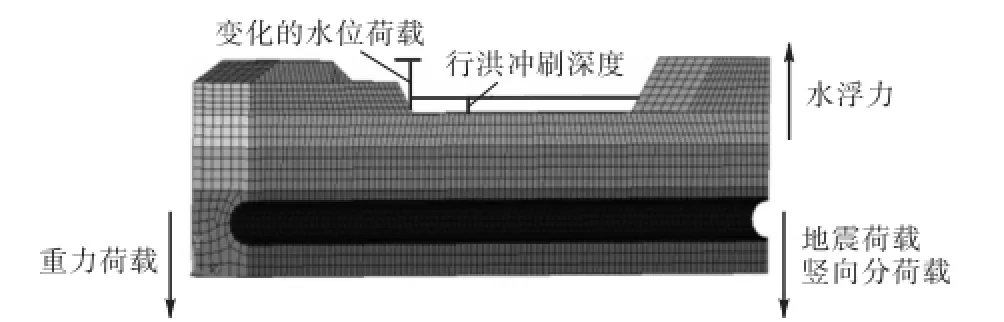
图4 模型荷载及离散示意Fig.4 Discrete and load schematic diagram of the model
穿江管道所受载荷主要包括结构自重、输油管道中油体重量等永久荷载,随冲刷变化的上覆土重量等可变荷载,地震载荷等偶然荷载.大河特征水位工况为防洪警戒水位4.5,m、常水位2.8,m和河道无水3种工况.工程所在地地质活动活跃,根据工程设计资料,地震设计烈度为Ⅶ度,地震荷载按照《建筑抗震荷载规范》[11]进行确立.
单位长度管道所受竖向地震荷载evkF计算式为

式中:vmx∂为竖向地震影响系数,根据工程地质条件,可取0.3;eqG为等效重量,此处取单位长度管道自重与管道中油体重量总和的0.75倍.
在数值模拟中,将不同工况下河道洪水位对应不同水荷载、水位变化引起的部分土层性质的变化、管道内部油体的有压及无压边界、按规范折算的地震荷载及河道行洪冲刷深度等转化成合理的APDL参数.优化过程中,程序会根据水位边界自动调节不同高度的土层参数;在APDL中/SOLU(加载与求解)部分施加边界条件以及上覆土重、地震荷载;使用生死单元技术逐步杀死土层单元,达到减小管道埋深效果的迭代过程中加入冲刷深度的影响;按照图4的流程进行迭代优化分析,求出最小埋深.
3.4 计算结果
位移及应力计算结果分别如图5和图6所示.当管道埋深较小时,可明显看出位于河道部分的输油管道向上凸起,有上浮破坏的趋势.从管道主应力云图可看出深色主要集中于管道上,在河道中间及管道隆起幅度较大的地方,拉应力较大.
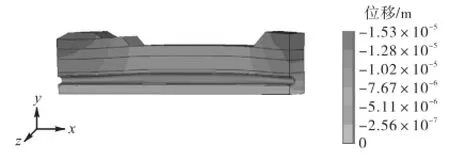
图5 管道竖直位移云图Fig.5 Nephogram of tunnel vertical displacement

图6 管道主应力云图Fig.6 Nephogram of tunnel principal stress
基于有限元优化算法,在管道竖直位移云图中,管道出现上浮趋势;在主应力云图中,管道周边开始出现拉应力,各项约束条件均得到满足时,程序迭代停止,此时的覆土深度即为管道抗浮最小埋深.
对于最小埋深的研究应选取不利抗浮稳定的工况.在对穿江管道工程的模拟中可不考虑油重、施工荷载等有利于管道抗浮稳定的因素.结合工程要求及计算效率,可在数值模拟中选用不同精度,即控制网格的疏密及埋深迭代值.通过优化埋深,迭代求出在大河常水位的不利工况下,不同精度对应的最小埋深值,对应表2可看出,在不同精度下,埋深的值在4.50,m左右;受计算精度的影响,优化的最小埋深各有差异,实际工程中可按照工程要求精度选取.对于本工程设计埋深要求精确到0.20,m,故选取0.20,m的精度.

表2 不同精度下有限元优化算法得到的最小埋深Tab.2 Minimum buried depth of different precisions by finite element optimization method
4 传统算法与有限元优化算法结果的对比分析
在对工程中抗浮最小埋深的分析中,传统算法较为简便,能够快速直观地得到最小埋深,但其未能考虑地质、复杂边界和地震荷载,尤其是对最小埋深影响很大的河道行洪冲刷因素.对于本工程,两者在不同特征水位下计算得到的最小埋深列于表3.

表3 各特征水位下最小埋深Tab.3 Minimum buried depth at feature water level
根据《给水排水工程顶管技术规程》[12]第5.4.2条要求:穿越江河水底时,覆盖层最小厚度不宜小于2.5,m;第5.4.3条要求:在有地下水地区及穿越江河时,管顶覆盖层的厚度尚应满足管道抗浮要求.由表3结果可看出传统算法与有限元优化算法得到的最小埋深均满足规范要求.但特征水位变化和河道冲刷对传统算法的最小埋深无影响,而对于有限元优化算法的结果则有影响.这是因为传统算法仅是上覆土体和管道自重与管道所受水浮力的比较,而有限元优化算法则考虑了特征水位的变化对边界条件的影响以及河道冲刷引起的上覆土层厚度减小对管道安全的影响.据此对于一些冲刷较大、边界条件复杂的类似工程宜采取有限元优化算法.
5 结 论
(1) 传统算法和有限元优化算法计算得到的管道最小埋深均符合相关规范规定,但前者求出的最小埋深不够准确,后者可以考虑上覆土层厚度、行洪冲刷、河道水位变化、地震荷载等因素的影响,可以得到更符合工程实际的结果.因此,在实际过程中应该同时采用这2种算法计算最小埋深,相互比较,综合确定用于设计的最小埋深.
(2) 对本文算例的穿江输油管道工程,使用有限元优化算法得到抗浮最小埋深为4.63,m.在该工程设计中实际选取的管道埋深为5,m,参考了本文模拟计算的结果.这也说明本文所提出的有限元优化算法在工程应用中是有其合理性的.
[1] Hagelia P. Semi-quantitative estimation of water shielding requirements and optimization of rock cover for sub-sea road tunnels [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1995,32(3):485-492.
[2] Thomas K,Gunther M. A numerical study of the effect of soil and grout material properties and cover depth in shield tunneling [J]. Computers and Geotechnics,2006,33(4/5):234-247.
[3] Dahlo T S,Nilsen B. Stability and rock cover of hard rock subsea tunnels [J]. Tunneling and Underground Space Technology,1994,9(2):151-158.
[4] Blom C B M,Horst E J V,Jovanovic P S. Threedimensional structural analysis of the shield-driven“Green Heart” tunnel of the high-speed line south [J]. Tunnelling and Underground Space Technology,1999,14(2):217-224.
[5] 李术才,徐帮树,丁万涛,等. 海底隧道最小岩石覆盖厚度的权函数法[J]. 岩土力学,2009,30(4):129-136.
Li Shucai,Xu Bangshu,Ding Wantao,et al. Weighted function method for minimum rock cover thickness of subsea tunnels [J]. Rock and Soil Mechanics,2009,30(4):129-136(in Chinese).
[6] 李树忱,张京伟,李术才,等. 海底隧道最小岩石覆盖厚度的位移收敛法[J]. 岩土力学,2007,28(7):162-166.
Li Shuchen,Zhang Jingwei,Li Shucai,et al. Displacement convergence method for minimum rock cover above submarine tunnel [J]. Rock and Soil Mechanics,2007,28(7):162-166(in Chinese).
[7] 中华人民共和国行业标准. JTG C30—2002 公路工程水文勘测设计规范[S]. 北京:中国水利水电出版社,2002. The Industry Standard of the People's Republic of China. JTG C30—2002 Hydrological Specifications for Survey and Design of Highway Engineering [S]. Beijing:China Water Conservancy and Hydropower Press,2002(in Chinese).
[8] Eisenstein Z. Large undersea tunnels and the progress of tunneling technology [J]. Tunneling and Underground Space Technology,1994,9(3):283-292.
[9] 戴小平,郭 涛,秦建设. 盾构机穿越江河浅覆土层最小埋深的研究[J]. 岩土力学,2006,27(5):101-105.
Dai Xiaoping,Guo Tao,Qin Jianshe. Research on minimum depth burial of shield tunnel machines crossing over ground base under rivers [J]. Rock and Soil Mechanics,2006,27(5):101-105(in Chinese).
[10] 刘元雪,施建勇,许 江,等. 盾构法隧道施工数值模拟[J]. 岩土工程学报,2004,26(2):239-243.
Liu Yuanxue,Shi Jianyong,Xu Jiang,et al. Numerical simulation of excavation of shield tunnel [J]. Chinese Journal of Geotechnical Engineering,2004,26(2):239-243(in Chinese).
[11] 中华人民共和国住房与城乡建设部. GB 50011—2010建筑抗震荷载规范[S]. 北京:中国建筑工业出版社,2010.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50011—2010 Code for Seismic Design of Buildings [S]. Beijing:China Architecture and Building Press,2010(in Chinese).
[12] 中国工程建设协会标准. CECS 246:2008 给水排水工程顶管技术规程[S]. 北京:中国计划出版社,2008.
China Association for Engineering Construction Standardization. CECS 246:2008 Technical Specification for Pipe Jacking of Water Supply and Sewerage Engineering [S]. Beijing:China Planning Press,2008(in Chinese).
Analysis of Minimum Buried Depth of Submerged Oil Pipeline for Anti-Uplift Stability
Qi Lan,Wang Pengsheng,Han Dong,Wang Wei
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Buried depth of submerged pipeline is affected and restricted by many factors. How to determine the minimum depth in the design is a key problem to be solved to ensure the safety. An optimal algorithm based on finite element method was proposed to overcome the shortcomings of traditional methods. The algorithm gives a comprehensive consideration of the thickness of overburden layers,erosion,earthquake load and other influencing factors to make the results more practical and reasonable. Comparison and analysis of the two methods through an engineering project show that finite element optimization method has the advantage of high efficiency.
finite element optimization method;minimum buried depth;submerged pipeline;anti-uplift stability
TU433
A
0493-2137(2013)04-0328-05
DOI 10.11784/tdxb20130407
2012-11-27;
2013-01-16.
国家青年科学基金资助项目(50909072).
戚 蓝(1955— ),女,博士,教授.
戚 蓝,lanqi0000@163.com.
