基于判别分析法室内悬浮颗粒物浓度与粒径分布测量*
2013-06-19刘红丽
刘红丽 周 雄 肖 磊
(武汉理工大学自动化学院 武汉 430070)
0 引 言
据调查,城市居民每天90%的时间是在各种室内环境中度过的[1],悬浮颗粒物是最重要的室内污染源之一,浓度与粒径大小是其重要特征.表征人体对颗粒物的暴露量的室内悬浮颗粒物浓度,不仅与颗粒物的数量有关,还与颗粒物的形态结构有密切的关系.从悬浮颗粒物的显微图片可以看出,颗粒物的边界复杂,表面粗糙,且大多数形态复杂,具有分形结构.若仅仅采用粒径难以准确描述颗粒物的形状,也不能准确计算出室内悬浮颗粒物的浓度极其粒径分布,因此还需要研究悬浮颗粒物的其他形态学参数如形状系数、分形维数等与其浓度之间的关系.
室内悬浮颗粒物浓度包括体积浓度、质量浓度和总表面积,其中质量浓度和总表面积必须要计算出单个颗粒物的体积和表面积的大小.对于标准形状的颗粒物而言,可采用一定的计算公式,但由于悬浮颗粒物的表面形状不规则,其表面积和体积不能用颗粒物的几何特征和物理特性的公式计算.因此,本文提出一种基于判别分析法室内悬浮的颗粒物粒形估计方法,将颗粒物近似为圆形、正方形,以及椭圆形等几种标准颗粒物形状等,以形状系数和分形维数作为颗粒物的观测数据,判断该颗粒物的形状与哪种标准形状的颗粒物最接近,并将待测颗粒物归类,利用该类标准形状的体积和表面积作为近似值,从而估算出该颗粒物的体积和表面积大小.
1 判别分析归类方法
判别分析法是在已知研究对象分成若干类型并已取得各种类型的一批已知样品的观测数据,根据某些准则建立判别式,然后对未知样品进行判别分类的方法.按照不同的判别准则,判别分析法可分为距离判别法、Fisher判别法、Bayes判别法和逐步判别法等.由于Bayes判别函数在正态等协差阵条件下可视为距离判别准则,不加权的Fisher判别法也可视为于距离判别法,且距离判别法对各类的分布无特定要求,因此本文采用距离判别法.距离判别法是根据已知分类的数据,分别计算各类的重心即平均值,判别准则是对任给的一次观测数据,若它与第k类的重心距离最近,就认为它来自第k类,从而实现颗粒物的分类.
将距离判别法应用在颗粒物粒形识别以及归类中,需要解决以下3个问题:(1)颗粒物形态学参数检测;(2)确定颗粒物的观测数据;(3)确定标准颗粒物的类.
要正确全面地描述颗粒物的形态,建立颗粒物浓度与粒径分布的数学模型,不仅需要基于颗粒物的数字图像识别颗粒物的颗粒物周长、面积,并计算单个颗粒物的粒径、形状系数分形维数[2].这些形态学参数的检测方法参考文献[3].
2 颗粒物测量指标的确定
颗粒物粒径、形状系数和分形维数从不同的侧面反映了颗粒物的形态,为研究颗粒边界三者之间的关系,选取了3种不同倍率,每种倍率获取6幅颗粒物显微图像,根据参考文献[3]中的算法分别计算了各个颗粒物的粒径、形状系数和分形维数,根据计算结果分析表明,随着颗粒物表面分形维数的增加,其形状系数呈减小趋势,但二者的线性关系较差[4].因为具有不同表面,不同投影轮廓的颗粒物,Feret最大径与最小径比值可能会有相同,而即使具有相同的Feret最大径与Feret最小径比值的颗粒物,并不一定有相同的表面分维数[5-7].
表1为6种颗粒物样品中各种颗粒表面分形维数及其形状系数的平均值,该表数据说明室内悬浮颗粒物的形状系数均值非常接近标准椭圆形颗粒物的参数值,80%的颗粒物的形状系数大于0.5.随着颗粒物粒径的增大,形状系数和分形维数都增大.颗粒物的分形维数基本在1.5以下,分形维数在1.10~1.20之间的颗粒物占绝大多数,这说明颗粒物的总体形态趋近于块状,而尖锐菱角、和长条形的颗粒物较少.颗粒物的形状在总体上是规则的,不规则的较少.当颗粒的形状系数越接近于1时,此颗粒的投影面形状越接近于圆.当颗粒的形状系数偏离1较远时,颗粒的投影面形状越不接近于圆形.
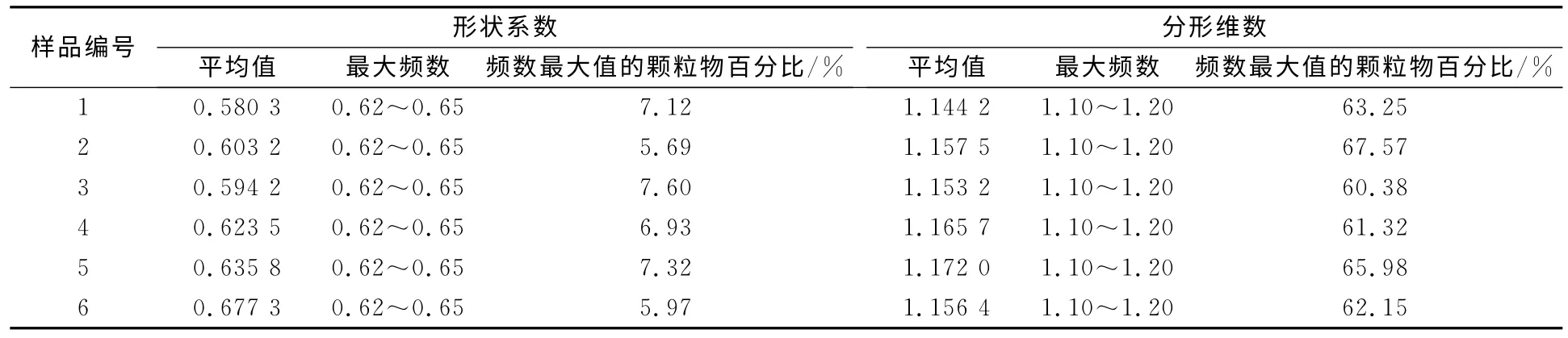
表1 颗粒物的形状系数与分形维数
分形维数越大,颗粒物表面越不规则,越粗糙,表面积就越大.随着颗粒物表面分维的增加分形维数越大,颗粒物表面越不规则越粗糙,表面积值就越大.随着颗粒表面分形维数的增加,形状系数则相应减少,二者具有良好的相关关系.由此可以推出颗粒表面分形维数与形状系数都可以表征颗粒物形状,并且具有良好的线性相关性.表面分形维数表征了颗粒物表面精细结构层次多少和自相似程度,值越大,颗粒物自相似程度就越大,精细结构越多,物体表面凹凸就越多,则形状系数越小,颗粒物形状越偏离圆形.因此在采用判别分析方法对颗粒物的粒形归类研究时,可以确定每个颗粒物形状系数与分形维数为测量指标.
为了得到颗粒物的类,需要计算出部分不同面积不同形状标准颗粒物的形状系数.对于标准颗粒物而言,形态系数在0.9~1.0之间的可近似于圆形,0.7~0.9之间的可近似于正方形,0.5~0.7 之间的可近似为正三角形,0.3~0.5 之间的可近似为狭长形及长方形,小于0.3的则为线形.由于颗粒物的总体形态趋近于块状,较少有尖锐菱角、长方形和长条形的颗粒物,在颗粒物图像处理中,由于区域填充,因此也不存在透明得颗粒物,故确定具有圆形、1∶2椭圆形、1∶2长方形和正三角形等粒形的标准颗粒物作为判别分析法所对应的颗粒物的类.
本文基于3种倍率下的颗粒物的形状系数和分形维数,并通过显微观察判断颗粒物的粒形,计算出各类形状系数和分形维数的均值和协方差.由于颗粒物在不同倍率下,其形状和信息都具有自相似性,因此将3种倍率下的数据融合一起作为不同颗粒物类的样本的观察数据,每一类抽取8个数据,见表2.
3 判别分析归类法的基本步骤
判别分析归类法实现颗粒物粒形归类的基本步骤如下.
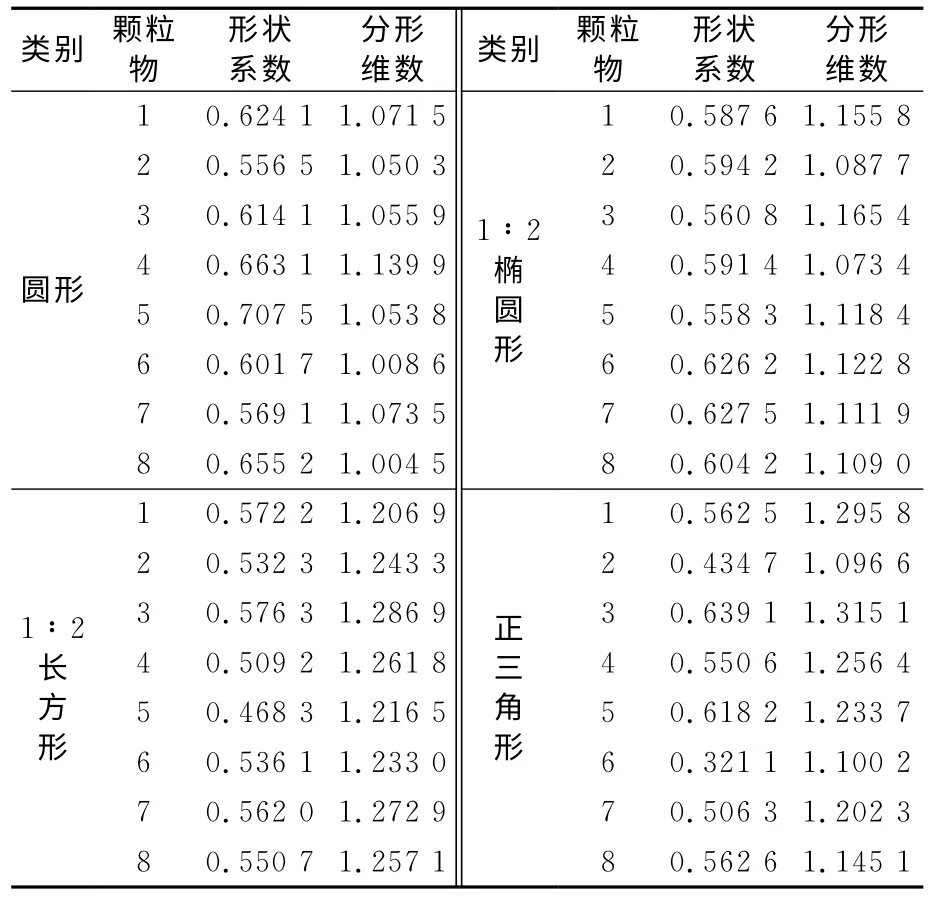
表2 不同颗粒物类的样本的观察数据
步骤1 检测已标记的颗粒物的最长尺寸为l,当2k-1<l<2k,k=1,2,3,…,则k的最大值为k.
步骤2 如果判断出k≤4,则很难确定这些小颗粒物的分形维数,因此可直接采用其形状系数作为样本观测数据实现颗粒物归类.用f 表示形状系数,则0.9≤f≤1.0时,该颗粒物直接归为圆形类,0.7≤f≤0.9时,归为正方形类,0.5≤f≤0.7时,归为正三角形类,0.3≤f≤0.5,归为1:2长方形类,0<f<0.3,归为线形类.
步骤3 如果判断出k>4,则以颗粒物的分形维数和形状系数为颗粒物样本的观测数据,分别计算表2中四类样本的均值、协方差阵.
步骤4 求判别函数W(x) 设m 个总体为G1,G2,…,Gm,它们的均值和协方差阵分别为μ(i),∑(i),i=1,2…,m,从每个总体Gi中抽取ni个样品,每个样品的观测数据有P个,记为X =(x1,x2,…,xp)′,X 到G1,G2,…,Gk总体的距离为D2(X,Gi)=(X-μ(i))′(∑(i))-1(X-μ(i)),则判别函数为
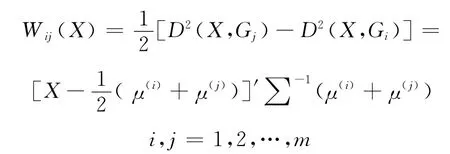
相应的判别准则为
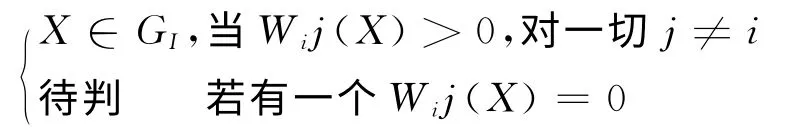
由此可以计算出
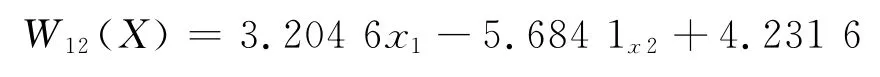
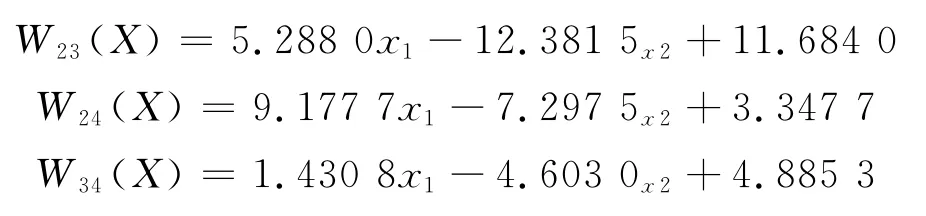
通过上述判别函数对表2中所有的颗粒物进行归类验证,结果全部判断正确.
步骤5 检验判别效果 判别分析是假设2组样品取自不同的总体,如果两个总体的均值向量在统计上差异不显著,则判别意义就不大.判别效果的检验就是检验两个总体的均值是否相等.检验的统计量为
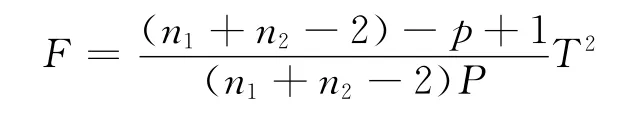
式中:P,n1,n2分别为每个总体观测数据的个数,2个总体的样本个数.其中
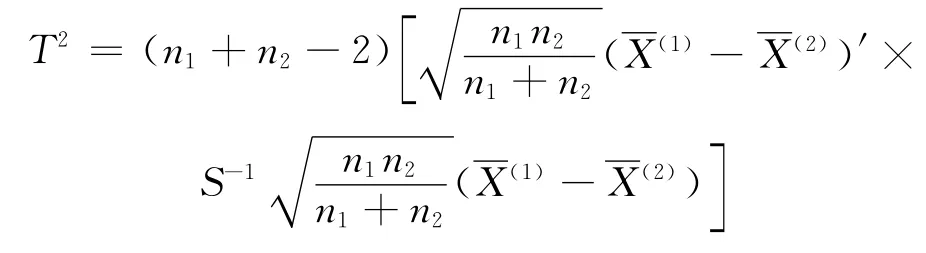
以2个总体为例进行计算得出
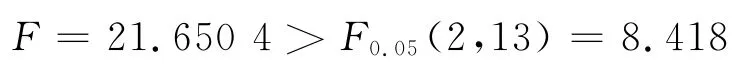
由此可以看出在α=0.05 的检验水平下,2总体间的差异显著,判别函数有效.其他几个判别函数检验结果同样也是有效的.
步骤6 对其他颗粒物样品分别进行判别归类统计.
4 实验结果分析
图1~3分别为基于判别分析法的室内悬浮颗粒物的数量浓度、质量浓度以及总面积及其粒径分布情况.从图中可以看出绝大部分悬浮颗粒物粒径在5μm 以下,且数量浓度的峰值均出现在颗粒物粒径1~2μm 之间.颗粒物的累积数量浓度与颗粒物粒径的双对数趋近于线性关系.颗粒物质量浓度的峰值与数量浓度和总表面积的峰值一样,都出现在1~2μm 之间,但总体质量的大部分是粒径大于5μm 的颗粒物.
5 结束语
以形状参数和分形维数为每一类的观测数据,提出了一种颗粒物判别分析归类的方法,基于图像处理技术计算得出室内悬浮颗粒物浓度和粒径分布的实验数据,并近似估计粒形、体积和表面积实现待测颗粒物归类,最后同时获取颗粒物的质量浓度、总表面积和体积浓度与粒径分布情况,这种方法克服了激光散射法、重量法等不能同时检测颗粒物粒形、浓度和粒径的缺点.
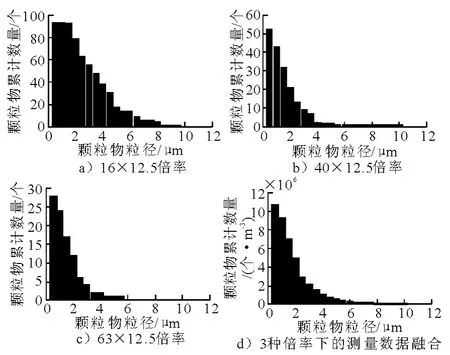
图1 颗粒物数量浓度累积分布
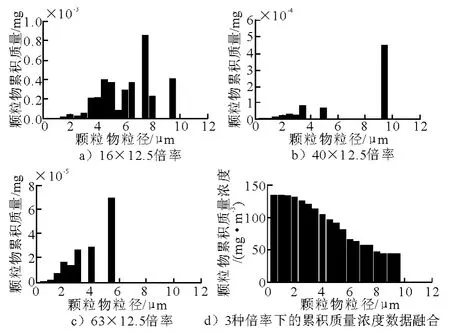
图2 颗粒物质量浓度分布

图3 颗粒物总表面积分布
由于研究对象是对颗粒物的二维图像,只能从图像中获取颗粒的二维参数,这不能足以完全描述颗粒物形态特征.在今后的研究工作中还需要通过颗粒图像的空域与时域的转换,对图像进行三维重建,建立单个颗粒物的三维模型研究分析颗粒物的三维特性,从而得到颗粒物更全面的形态学参数,实现颗粒物的科学分类.另外由于目前在解释室内悬浮颗粒物的来源上还存在许多的问题,对不同来源的颗粒物形态特征的研究很少,因此必须获取大量颗粒物的行显微图像,研究速度更快的图像处理和辨识算法,计算单个颗粒物的形态学参数,建立他们之间的关联矩阵,从而确定颗粒物的类,使相同类中颗粒物粒形相似,来源相近,提高颗粒物浓度和粒径分布测量精度.
[1]THATCHER T L,LAI A C K,RPSA M J,et al.Effects of room furnishings and air speed on particle deposition rates indoors[J].Atmospheric Environment,2002,36(11):1811-1819.
[2]刘红丽,张 伟,李昌禧.室内可吸入颗粒物浓度与粒径分布检测方法的研究[J].仪器仪表学报,2009,30(2):340-344.
[3]MORA C F,KWAN A K H.Sphericity,shape fator and convexity measurement of coarse aggregate for concrete using digital image processing[J].Cement and Concrete Reseach,2003,33(3):351-358.
[4]HARRIS S J,MARICQ M M.Signature size distributions for diesel and gasoline engine exhaust particulate matter[J].J.of Aerosol Science,2001,32(7):749-764.
[5]刘红丽.室内悬浮颗粒物浓度与粒径分布测量方法的研究[D].武汉:华中科技大学,2009.
[6]PARK S U,KIM J W.Aerosol size distributions observed at the Seoul National University campus in korea during the dust asian and non-asian dust periods[J].Atmospheric Environment,2006,40(91):1722-1730.
[7]王赞红.近地面大气颗粒物粒度与粒形特征[J].环境科学,2007(9):55-58.
