基于云遗传算法优选的SVR 交通量预测模型＊

康海贵 莫仁杰 李明伟

（大连理工大学港口、海岸及近海工程国家重点实验室 大连 116024）

交通堵塞、交通拥挤及交通事故等问题使得城市的交通系统不堪重负.短时交通量预测是城市动态交通分配和交通诱导系统的关键技术，对解决城市交通问题具有重要意义，是智能交通领域的研究热点.商蕾［1］在构建城市道路微观交通仿真模型框架的基础上，运用面向对象思想和技术、动态内存管理和实时视景仿真技术开发了城市道路微观交通流仿真原型系统.孙立光等［2］提出了包含傅里叶历史估计、自回归和邻域回归3个子模型的应用于流量和速度预测的组合预测模型.张杰等［3］应用交通流一维元胞自动机模型进行仿真试验，研究理论交通流的混沌现象.张敬磊等［4］针对智能交通系统的开发和交通流特性，应用小波Mallet分解算法建立交通流状态辨识方法.支持向量回归机模型（support vector regression，SVR）采用结构风险最小化原则替代经验风险最小化原则，能在模型的复杂性和学习能力之间寻求最佳折中［5］.由于其出色的学习能力和泛化性能，在短时交通流量预测方面得到了广泛的应用［6］.而SVR 模型本身并未给出模型最优参数组合的选择方法，常用的经验选取法和交叉试算法存在一定缺陷［7］.遗传算法［8］（genetic algo－rithms，GA）具有全局寻优、鲁棒性和自适应性强等优点［9］，可应用于模型参数的优选.本文基于混沌logistic映射的遍历性、初值敏感性、不容易陷入小循环和不动点的优势，同时借以云模型云滴的随机性和稳定倾向性特点，对标准遗传算法进行改进，建立了基于混沌云遗传算法（chaos cloud genetic algorithm，CCLGA）进行参数优选的CCLGA－SVR 短时交通流量预测的新方法.通过数值模拟，证明了该方法的有效性，可为短时交通管理提高依据.

1 基于ε损失函数的SVR

设变 量y 与x 遵循某一未知联合概率F（x，y），SVR回归就是寻求实值函数f（x）＝w·φ（xi）＋b来拟合以观测样本集S ＝｛（x1，y1），（x2，y2），…，（xl，yl）｝，使得风险R［f］＝∫C（x，y，f）dρ（x，y）最小.式中：C 为损失函数.回归时观测值与预测值之间的误差用ε不敏感函数｜yi－f（xi）｜ε＝max｛0，｜yi－f（xi）｜－ε｝来度量，当x点的观察值y与预测值f（x）之间的误差不超过小正数ε时认为函数对这些样本点的拟合是无差错的.基于ε损失函数SVR 问题可表示为

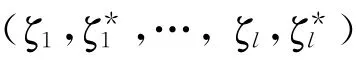
SVR 回归模型中有需要给定C，v 及核函数K 中的参数，这些参数的选取对模型结果精度、稳定性和泛化性有重要影响.参数的选取直接决定着模型的使用性能，实际应用中往往是凭经验选取或用交叉验证法选取，2种方法中前者经验性太而且在模型精度上仍有待提高，后者模型参数寻优方向不明显、计算量大，当个体的数量增加时计算量则是指数性增长、计算耗时.

2 混沌云遗传算法

2.1 混沌理论

混沌优化方法是利用混沌遍历及初值敏感等性质作为全局优化机制.混沌优化方法中常用Logistic混沌映射，Logistic映射产生的混沌序列的概率密度服从两头多中间少的切比雪夫分布，其遍历性解释见文献［10］.一维Logistic映射方程为xn＋1＝u·xn·（1－xn）.式中：xn∈［0，1］，u∈［0，4］，n＝0，1，2，….xn是混沌变量x 在第n次的迭代值，u是控制参量.为保证混沌变量对初值的遍历性及敏感性n 值一般取［400～1000］；x0取［0，1］区间内除0.25，0.5，0.75 以外的初值.实验证明，当u＝4 时系统完全处于混沌状态［11］，此时按映射方程得出的混沌变量可以遍历到整个搜索区域.图1为n＝50000，u＝4，x（0）＝0.45时混沌变量分布，图2给出变量500次迭代分布情况.从图1和图2可以看出，Logistic混沌映射轨道点能够布满整个区域的内部和边界，并且区域边界轨道点数量较多内部点数量较少但整体分布较均匀的特点.

2.2 云理论

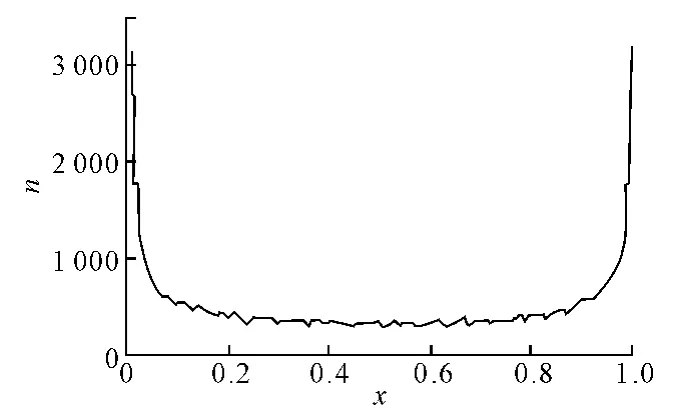
图1 Logistic映射混沌变量图

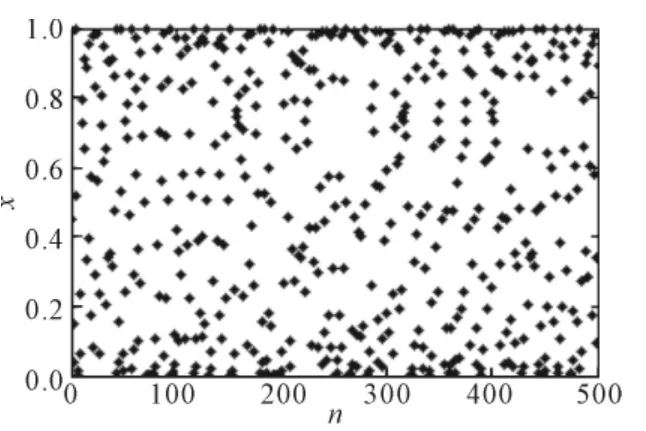
图2 变量迭代分布图

设T 为论域u 上的语言值，映射CT（x）：u→［0，1］，x∈u，x→CT（x），则CT（x）在u上的分布称为T 的隶属云，简称云［12］，当CT（x）服从正态分布时，称为正态云模型.云理论模型［13］是语言值表示不确定性的转换模型，具有随机、模糊及稳定等特性.云模型［14］的整体特性可以用期望E、熵S、超熵H 这3个数字特征来表示.基本正态云如图3所示，图中E 是云滴在论域空间分布的期望；S 代表定性概念的可度量粒度；H 是熵的不确定性度量即熵的熵.云模型在知识表达时的不确定中带稳定性特点，其期望E 可以代表父代个体遗传的优良特征，是子代对父代的继承，熵S和超熵H 表示了继承过程的不确定性和模糊性，表现了物种进化过程中的变异特征，算法进化的随机性可以避免搜索陷入局部极值，而稳定倾向性又可以很好地定位全局最优值.

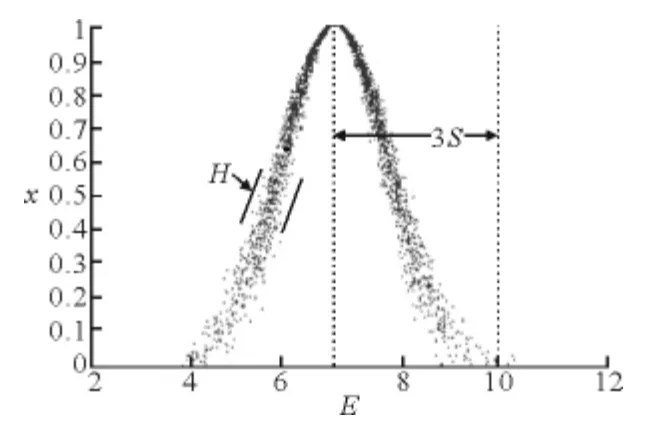
图3 正态云模型示意图

2.3 CCLGA算法

CCLGA 算法是基于“保护”较优个体，快速进化较差个体的思想，基本思路是运用混沌Logistic映射产生初始种群，利用云模型指导算法进行交叉和变异操作，进化到一定程度时，做微小的混沌扰动生成新的种群，重新进行优选迭代，直到满足终止条件为止.CCLGA 算法设计步骤如下.

步骤1 混沌Logistic映射生成m 个体的初始种群.

步骤2 计算每个体的适应度值，记录最大个体染色体及其适应度值.

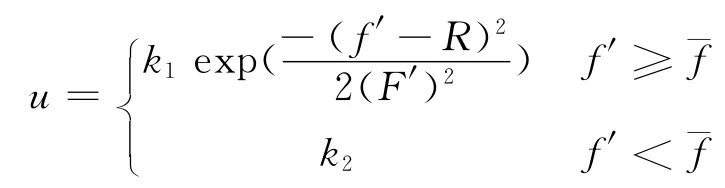
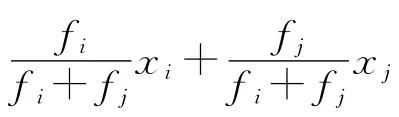
步骤6 将经过交叉生成的新个体和经过变异生成的新个体组合得到新的种群，转入步骤2）进行下一轮的迭代计算，直到满足停止条件，其中c1－c4为控制参数，本文取c1＝c3＝2.5p（p 为种群的大小），c2＝c4＝15.

3 CCLGA 算法优选的SVR模型

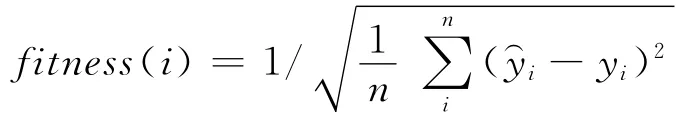
4 交通量时空分析及预测方法

本文模型预测以某市交通频繁堵塞路段高峰期（17：00～20：00）为例，区域路网简化如图4所示.根据路段长度及平均行车速度取交通量数据采样周期为10 min（时段长度确定为10 min），7d共采集数据126组.

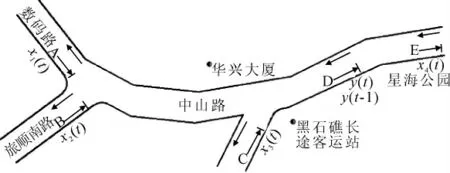
图4 区域道路简化图

图4中，以D 断面交通流量为预测目标集，其交通流量受到上游断面A，B，C，及下游E 断面流量的直接影响.X1（t），X2（t），X3（t），X4（t）分别为断面A，B，C，E 处t 时段的交通流量，Y（t－1），Y（t）分别为预测断面D 处的t－1和t 2个时段交通流量，Y（t＋1）为该断面t＋1时段的流量.天气因素设为第六个影响因素X5（t），其量化方法为大雪或大雨雪为1，小雪或小雨雪为0.75，大雨为0.5，小雨为0.25，晴或多云为0.因此，得影响断面D 处给定方向t＋1时段交通流量Y（t＋1）的7 个影响因素X＝｛X1（t），…，Y（t－1），Y（t）｝，将其作为模型的输入向量，模型的输出量值为Y＝｛Y（t＋1）｝.由于周末高峰期车流量集中现象与工作日高峰期的特征有所差别，本文只选周一至周五为研究对象，将前4d晚高峰时段数据作为模型的训练样本，将第5d晚高峰时段后16组数据作为检验样本进行仿真预测.

5 交通量预测模型仿真实验

为分析模型全局寻优性能和预测精度，以控制寻优时间的方式对模型进行仿真.CCLGASVR 模型，经过迭代优选得到全局参数最优组合为C＝584.5，ν＝0.8763和δ＝0.2197；运用不同对比模型进行仿真计算，得不同模型预测结果对比见表1，预测相对误差曲线见图5.

表1 不同预测模型仿真结果对比 ／辆

表2 不同算法寻优过程适应度对比

图6 算法适应度变化对比

不同参数优选模型在限定时间内寻优性能对比如表2所列；模型搜索的适应度函数值随时间的变化曲线如图6所示.方面优 于NF－SVR 模型，SGA－SVR 模型 优 于 基本的GA－SVR 模型，CCLGA－SVR 模型在限定时间内寻优速度及模型精度优于SGA－SVR 模型.在一定的运行时间（2000s）内，SGA 算法搜索到的个体的适应度普遍大于GA 算法；CCLGA 算法搜索到个体的适应度普遍大于GA 算法和SGA 算法.

6 结束语

由模型寻优搜索过程、寻优效率曲线以及预测输出结果可看出：（1）在逼近原始流量序列方面，SVR 的预测方法明显优于PSO－BP神经网络模型；（2）基本的GA－SVR 模型在参数寻优性能

本文提出了模型参数选取的新方法（CCLGA算法），与NF 交叉验算法、基本GA 算法以及传统SGA 算法相比，CCLGA 算法在规定的时间内搜索效率更高，更适合系统利用新的数据进行模型参数的自动更新，有效降低陷入局部最小化风险，取得精度较高的模型输出.

综合考虑了城市短时交通流的时空分布特性及天气影响因素，共7 个影响因子，将CCLGASVR 模型应用于城市短时交通流量预测，可以减少短时交通流预测的用时并提高预测精度和可靠度，为城市复杂交通环境下交通管理提供可靠的技术服务.实际应用中，可以根据实时预测结果，动态修改和实时发布未来几个时段内的交通预测信息，通过调节交通指示等手段，可有效缓解整个交通网络的拥堵状况.

［1］商 蕾.城市道路交通流仿真系统研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（3）：587－590.

［2］孙立光，李瑞敏，董 屾，等.短时交通流组合预测模型研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（5）：874－876.

［3］张 杰，贺国光.基于一维元胞自动机模型的交通流混沌研究［J］.武汉理工大学学报：交通科学与工程版，2009，33（1）：34－36.

［4］张敬磊，王晓原.交通流状态辨识小波算法研究［J］.武汉理工大学学报：交通科学与工程版，2006，30（5）：820－823.

［5］VAPNIK V.The nature of statistical learning theory［M］.New York：Springer，1995.

［6］刘艳忠，邵小健，李旭宏.基于Lagrange支持向量回归机的短时交通流量预测模型的研究［J］.交通与计算机，2007，5（25）：47－50.

［7］YAN H S，XU D.An approach to estimating product design time based on fuzzy－support vector machine［J］.IEEE Transactions on Neural Networks，2007，18（3）：721－731.

［8］孙月峰，张胜红，王晓玲，等.基于混合遗传算法的区域大系统多目标水资源优化配置模型［J］.系统工程理论与实践，2009，29（1）：139－142.

［9］MIN S H，LEE J，HAN I.Hybrid genetic algorithms and support vector machines for bankruptcy prediction.Expert Systems with Applications，2006，31（3）：652－660.

［10］李祥飞.混沌优化理论在控制系统设计中的研究［D］.长沙：中南大学，2003.

［11］LU Q Z，SHEN G L，YU R Q.A chaotic approach to maintain the population diversity of genetic algorithm in network training［J］.Computational Biology and Chemistry，2003，27（3）：363－372.

［12］刘常昱，李德毅，杜 鹢，等.正态云模型的统计分析［J］.信息与控制，2005.3，34（2）：236－239.

［13］李兴生.基于云模型和数据场的分类和聚类挖掘研究［D］.南京：中国人民解放军理工大学，2003.

［14］WANG Shuliang，LI Deren，SHI Wenzhong.Cloud model－based spatial data mining［J］.Geographical Information Science，2003，9（2）：77－78.